陪集与 Lagrange 定理

陪集 (coset)

设群 `H le G`, `a in G`, `a H := {a h | h in H}`, `quad H a := {h a | h in H}` 分别称为 `H` 关于 `a` 的左陪集和右陪集. 左陪集 `a H` 是 `H` 中全体元素在左平移变换 `l_a: h to a h` 下的像. 一般情况下, 陪集并不是 `G` 的子群.

以下主要讨论左陪集, 右陪集是完全类似的.

整数加群 `ZZ` 中, 子群 `3ZZ` 表示所有 3 的倍数. 它的陪集有 3 个: `3 ZZ`, `3 ZZ + 1`, `3 ZZ + 2`, 每个陪集中的元素是模 3 同余的.

群 `G` 中, 子集的乘积和逆分别定义为 `H K = {h k | h in H, k in K}`, `quad H^-1 = {h^-1 | h in H}`; 显然 `H le G` 当且仅当 `H H = H` 且 `H^-1 = H`.

设群 `H le G`, `a, b in G`, 则 `b in a H` `iff a H = b H` `iff a^-1 b in H`. 它们都描述了同一件事: `a, b` 相差一个 `H` 中的因子.

用元素的语言:
1. `rArr` 2. 由 `b in a H` 知 `EE h in H` 使 `b = a h`, `a = b h^-1`. 任取 `a h_1 in a H` 有 `a h_1 = b h^-1 h_1 in b H`; 另一方面, 任取 `b h_2 in b H` 有 `b h_2 = a h h_2 in a H`, 所以 `a H = b H`.
2. `rArr` 3. 任取 `a h_1 in a H`, 则 `EE h_2 in H` 使 `a h_1 = b h_2`. 所以 `a^-1 b = h_1 h_2^-1 in H`.
3. `rArr` 1. 因为 `a^-1 b in H`, 所以 `b = a a^-1 b in a H`.

用集合的语言:
1. `rArr` 2. 由 `b in a H` 有 `b H sube (a H) H = a H`; 另一方面, 由 `b in a H` 知 `a in b H^-1 = b H`, 用类似的论证得 `a H sube b H`, 故 `a H = b H`.
2. `rArr` 3. 由 `a H = b H` 得 `b^-1 a in H H^-1 = H`.
3. `rArr` 1. 同时左乘 `a` 即可.

数论中的例子: `a H` 表示所有模 `n` 余 `a` 的整数, 则 `b in a + n ZZ` `iff a + n ZZ = b + n ZZ` `iff b - a in n ZZ`. "陪集" 是 "剩余" 的概念在群论的延伸.

子群 `H` 确定的陪集划分 设 `H` 是 `G` 的子群, 如果我们把相差一个 `H` 中因子的 `a, b` 视为相等, 即, 定义 `sigma_H^l`: `a ~ b iff a H = b H`, 可以验证 `sigma_H^l` 构成 `G` 上的等价关系, 称为 `G` 上的一个同余. 因为 `b ~ a` 当且仅当 `b in a H`, 所以 `a in G` 所在的等价类就是 `a H`. 该等价关系给出 `G` 上的划分: `pi_H^l := { a H | a in G }`. 类似地, `H` 的右陪集确定了等价关系 `sigma_H^r` 和相应的划分 `pi_H^r`.

在有限群 `G` 中, 任意元素属于且仅属于下面的一个陪集: `H, a_1 H, a_2 H, cdots, a_n H`. 其中只有 `H` 是子群, 其它的陪集不含单位元, 因而不构成子群. 我们将很快看到, 陪集的结构和 `H` 非常类似, 它是 `H` 在平移变换下的像, 是 `H` 在 `G` 中的“陪衬”.

Lagrange 定理

陪集有多少个? 每个陪集中有多少元素? Lagrange 定理可以回答这些问题.

子群 `H` 在 `G` 中左右陪集数相等, 称为它的指数 `[G : H] := |pi_H^l| = |pi_H^r|`.

为证明两个集合基数相等, 我们构造它们之间的双射. 作 `varphi: a H in pi_H^l to H a^-1 in pi_H^r`. 由 `a H = b H iff a^-1 b in H` `iff b^-1 (a^-1)^-1 in H` `iff H a^-1 = H b^-1` 知, `varphi` 为一映射, 且为一单射. 又, 关于任意 `H a in pi_H^r`, `a^-1 H` 是其原像, 从而 `varphi` 为一满射. 所以 `varphi` 为双射.

子群 `H` 的每个陪集大小相同, 即 `AA a in G`, `|a H| = |H a| = |H|`. 这说明陪集对群的划分是均匀的.

考虑左平移变换 `l_a: h in H to a h in a H`. 显然它是满射. 又因为群上的左平移变换是单射 (根据消去律), 所以 `l_a` 是双射, `|H| = |a H|`. 同理 `|H| = |H a|`.

Lagrange 定理 令 `G` 为一有限群, `H le G`, 则由两个引理, `G` 的大小等于每个陪集的大小乘以陪集数, 即 `|G| = [G : H] |H|`. 因此, `G` 的任意子群的阶和指数都整除 `|G|`. 特别 `G` 的任意元素 `a` 的阶都整除 `|G|` (考虑 `a` 生成的循环群, 该子群的阶等于 `|a|`, 且整除 `|G|`).

素数阶群是循环群.

设 `|G| = p` 为一素数. 任取非单位元 `a in G`, 则 `|a| != 1`, 由 Lagrange 定理, `|a| = p`, 故 `(:a:) = G`.

正规子群与商群

正规子群

一般来说, 由于群的乘法未必可交换, 左, 右陪集 `a H, H a` 是不相等的. 但如果它们相等的话, 会带来许多好的性质, 这就引出正规子群的定义.

如果 `G` 的子群 `H` 满足 `AA a in G`, `a H = H a`, 则称 `H` 为 `G` 的一个正规子群 (normal subgroup, 或不变子群, 或自共轭子群), 记为 `H normal G`.

正规子群的定义可以减弱为: `H` 的每一个左陪集都是一个右陪集, 即 `(AA a in G)` `(EE b in G)` `a H = H b`. 事实上, 由 `a in a H = H b` 知 `H b = H a` 这就证明了那个存在的右陪集其实就是 `H a` 自己.

正规子群的等价条件 令 `H` 是 `G` 的子群, 则下列各款等价:
1. `H normal G`;
2. `(AA a in G)` `a H a^-1 = H`; 这就是正规子群又称自共轭子群的原因;
3. `(AA a in G)` `a H a^-1 sube H`; 这是实用的判定条件, 也可以写成 `G H G^-1 sube H`.

1. `rArr` 2. `AA a in G`, 由 `a H = H a` 知 `a H a^-1 = H a a^-1 = H`.
2. `rArr` 3. 显然.
3. `rArr` 1. `AA a in G`, 由 `a H a^-1 sube H` 同时右乘 `a` 有 `a H sube H a`; 另一方面, 由 `a^-1 H (a^-1)^-1 sube H` 同时左乘 `a` 有 `H a sube a H`. 于是 `a H = H a`.

正规子群是由若干不相交共轭类组成的. 为寻找一个群的正规子群, 可以从共轭类着手.

1. `G`, `{e}`, 是 `G` 的两个平凡正规子群;
2. 群的中心 `Z(G)` 是正规子群;
3. Abel 群的任一子群都是正规子群;
4. `SL_n(bbb F) normal GL_n(bbb F)`.
5. `2n` 阶群中, `n` 阶子群是正规子群, 如 `A_n normal S_n`. 不是所有 `2n` 阶群都有这样的子群, 如, 后面将证明 `A_5` 只有平凡正规子群, 但它的确是偶数阶 (60) 的.

5. 任取 `g in G\\H`, 则 `g H != H`, 因此 `g H = G\\H`. 同理 `H g = G\\H`, 因此 `g H = H g`.

令 `G, H` 为两个群, `f: G to H` 为群同态, 则 `G_1 normal G rArr f(G_1) normal f(G)`,
`H_1 normal H rArr f^-1(H_1) normal f^-1(H) = G`.

由子群的相关定理, 有 `f(G_1) le f(G)`, `f^-1(H_1) le G`. 下面只需验证子群的正规性. `AA h in f(G)`, 存在 `g in G` 使 `f(g) = h`. 从而由 `G_1 normal G` 知 `h f(G_1) h^-1 = f(g) f(G_1) f(g)^-1 = f(g G_1 g^-1)` `= f(G_1)`, 所以 `f(G_1) normal f(G)`.
另一方面, 由集合论的等式有 `f(f^-1(H_1)) sube H_1`. 从而由 `H_1 normal H` 知 `AA g in G`, `f(g f^-1(H_1) g^-1) sube f(g) H_1 f(g)^-1 = H_1`, 即 `g f^-1(H_1) g^-1 sube f^-1(H_1)`, 因此 `f^-1(H_1) normal G`.

群同态的核是正规子群: `"Ker"f = f^-1(e_H) normal G`.

令 `G` 为一群, `H, K` 是 `G` 的两个子群, 则
1. `H normal G` `rArr H nn K normal G nn K = K`;
2. `H normal G and H le K le G` `rArr H normal K`.
3. `H normal G or K normal G` `rArr H K le G`;
4. `H normal G and K normal G` `rArr H K normal G`;
5. `H normal G and K normal G` `rArr H nn K normal G`;

1. 显然 `H nn K le K`; 由 `H normal G` 知 `K (H nn K) K^-1 sube G H G^-1 = H`, 又 `K (H nn K) K^-1 sube K`, 所以 `K (H nn K) K^-1 sube H nn K`, 即 `H nn K normal K`.
2. 这是显然的, 因为 `AA a in K sube G`, `a H = H a`. 当然, 也可以由 1. 得到: `H normal G` `rArr H nn K normal G nn K`, 即 `H normal K`.
3. 不妨设 `H normal G`. 任取 `h k in H K`, 其中 `h in H`, `k in K sube G`, 则 `h k in H k = k H sube K H`, 因此 `H K sube K H`. 同理 `K H sube H K`, 因此 `H K = K H`. 从而由子群的积是子群的充要条件知 `H K le G`.
4. 由 3, `H K le G`, 从而由 `H, K normal G` 知, `AA g in G`, `g (H K) = (g H) K = (H g) K = H (g K)` `= H (K g) = (H K) g`. 因此 `H K normal G`.
5. 显然 `H nn K le G`; 由 `H, K normal G` 知 `G (H nn K) G^-1 sube G H G^-1 = H`, `G (H nn K) G^-1 sube G K G^-1 = K`, 因此 `G (H nn K) G^-1 sube H nn K`, 即 `H nn K normal G`.
   

从群中选出一个正规子群的过程好比选举班干部: 比如 `H le K le G`, 如果 `H normal G`, 代表 `H` 的“正规性”已经在 `G` 中得到认可, 那么 `H` 在 `G` 的子群 `K` 中自然也是正规的, 即 `H normal K`.

子群的正规性一般不具有传递性, 即 `K normal H normal G` 未必推出 `K normal G`.

from sympy.combinatorics import Permutation, PermutationGroup
g = PermutationGroup(Permutation(1,2)(3,4), Permutation(1,3)(2,4), Permutation(1,4)(2,3))
g.order() # 4
g.is_abelian # True

商群

令 `G` 为一群, `N normal G`. 易知上节定义的 `pi_N^l = pi_N^r`. 现在定义 `G // N := pi_N^l = {a N | a in G}` 上的二元合成 `*` 如下 `a N * b N := (a b)N`. 可以验证 `*` 是映射, 因此是一个二元运算. 且 `G//N` 关于 `*` 成一群, 称其为 `G` 关于 `N` 的商群 (factor group). 直观上, 商群是将正规子群 `N` "收缩" 或 "粘合" 为一个点 (单位元) 后得到的群.

映射的良定义验证: `a_1 N = a_2 N`, `b_1 N = b_2 N` `rArr (a_1 b_1) N = a_1 (b_1 N)` `= a_1 (b_2 N) = a_1 (N b_2)` `= (a_1 N) b_2 = (a_2 N) b_2` `= a_2 (N b_2) = a_2 (b_2 N)` `= (a_2 b_2) N`. 群的验证: 封闭性: 显然; 幺元: `N`; 逆元: `(a N)^-1 = a^-1 N`; 结合律: `(a N*b N)*c N = (a b)c N = a(b c)N = a N*(b N*c N)`.

设群 `N normal G`, 则 `G//N = {bar e} iff N = G`.

设群 `N normal G`, 映射 `eta: a in G to a N in G//N` 是满同态, 称为自然同态.

设群 `N normal G_1`, `N normal G_2`, 且 `G_1 le G_2`. 则 `G_1 normal G_2 iff G_1//N normal G_2//N`.

取自然同态 `eta: G_2 to G_2//N`.
"`rArr`". 由同态像保持正规子群的关系, `G_1 normal G_2 rArr eta(G_1) normal eta(G_2)`, 即 `G_1//N normal G_2//N`.
"`lArr`". 只需验证 `G_1//N` 在自然同态 `eta` 下的原像 `eta^-1(G_1//N) = G_1`. 由 `eta(G_1) = G_1//N`, 有 `G_1 sube eta^-1(G_1//N)`, 反之设 `g in G_2`, `g N in G_1//N`, 则存在 `g_1 in G_1`, 使 `g N = g_1 N`, 即 `g in g_1 N sube G_1`. 从而 `eta^-1(G_1//N) sube G_1`. 于是 `G_1//N normal G_2//N rArr eta^-1(G_1//N) normal eta^-1(G_2//N)`, 即 `G_1 normal G_2`.

由 Lagrange 定理, 当 `|G| lt oo` 时 `|G // N| = |G| // |N|`.

商群相关的映射, 常常需要验证其映射的良定义. 不过, 商群相关的映射又常常显然是满射. 这就简化了证明.

群同态基本定理, 两个同构定理

令 `f: G to H` 为一群同态映射, 则 `f` 可分解为一群满同态映射 `h` 和一群单同态 `g` 映射的合成, 即 `f = g @ h`.

构造性证明: 易知 `"Ker"f normal G`. 作 `h: a in G to a "Ker"f in G//"Ker"f`,
`g: a "Ker"f in G//"Ker"f to f(a) in H`. 则由, `h` 为一满同态. 而 `g` 为一单同态. 事实上, 由 `a "Ker"f = b "Ker"f` `iff f(a) = f(b)` `iff g(a "Ker"f) = g(b "Ker"f)` 知, `g` 为一映射, 且为单射, 另外 `g(a"Ker"f * b"Ker"f)` `= g((a b)"Ker"f) = f(a b)` `= f(a) f(b) = g(a"Ker"f) g(b"Ker"f)`, 所以 `g` 为一同态. 最后, 容易看出 `f = g @ h`.

联系集合论中的定理: 令 `f: A to B` 为一映射, 则 `f` 可分解为一满射 `h: A to C` 和一单射 `g: C to B` 的合成, 即 `f = g @ h`.

群同态基本定理 令 `f: G to H` 为一群同态映射, 则 `G//"Ker"f ~= "Im"f`. 定理告诉我们, 正规子群与相应的商群总是可以看作同态的核与像.

由引理, `f` 有分解 `f = g @ h`, `g` 是到 `"Im"f` 的满射. 因此 `g` 为到 `"Im"f` 的同构映射.

令 `f: G to H` 为一群同态映射, 则 `AA G_1 le G`, `f^-1(f(G_1)) = G_1` 当且仅当 `"Ker"f le G_1`.

若 `f^-1(f(G_1)) = G_1`, 显然 `"Ker"f` 为一群, 因此只需证 `"Ker"f sube G_1`. 则 `"Ker"f = f^-1(e_H) sube f^-1(f(G_1)) = G_1`. 反之, 令 `"Ker"f le G_1`. 由集合论的知识知道, 恒成立 `f^-1(f(G_1)) supe G_1`, 因此只需证 `f^-1(f(G_1)) sube G_1`. `AA a in f^-1(f(G_1))`, 存在 `b in G_1`, 使 `f(a) = f(b)`, 从而 `e_H = f(a)f(b)^-1 = f(a b^-1)`, 即 `a b^-1 in "Ker"f le G_1`, 因此 `a = (a b^-1) b in G_1`, 即 `f^-1(f(G_1)) sube G_1`.

令 `f: G to H` 为一群满同态映射, `S = {G_1 | "Ker"f le G_1 le G}`,
`S_1 = {H_1 | H_1 le H}`. 则 `|S| = |S_1|`, 即 `G` 中含 `"Ker"f` 的子群与 `H` 中的子群一一对应.

作 `eta: G_1 in S to f(G_1) in S_1`, 则由子群在群同态映射下的像也为一子群知, `eta` 为一映射. 任取 `H_1 in S_1`, 则 `f^-1(H_1) in S` (注意 `"Ker"f = f^-1(e_H) sube f^-1(H_1)`), 且由 `f` 为满射知, `f(f^-1(H_1)) = H_1`. 故 `eta` 为一满射. 根据, `f(G_1) = f(G_2) iff f^-1(f(G_1)) = f^-1(f(G_1))` `iff G_1 = G_2`. 从而 `eta` 为一单射, 于是 `eta` 为一双射.

由正规子群在满同态映射下的像和原像也是正规子群知, 将上述引理的子群换成正规子群, 结论也成立.

第一同构定理 令 `f` 是群 `G` 上的同态映射, `H` 是 `G` 的含 `"Ker"f` 的正规子群, 则 `G//H ~= f(G)//f(H)`.

显然 `f(H) normal f(G)`. 作 `eta: a H in G//H to f(a) f(H) in f(G)//f(H)`. 由 `a H = b H` `iff a^-1 b in H` `iff f(a^-1 b) in f(H)` `iff f(a)^-1 f(b) in f(H)` `iff f(a) f(H) = f(b) f(H)` (其中由 `f(a^-1 b) in f(H)` 得出 `a^-1 b in H`, 利用了) 知, `eta` 为一映射, 且为一单射. 又显然 `eta` 为满射. 从而 `eta` 为一双射. 又 `eta(a H b H) = eta((a b) H) = f(a b)f(H)` `= (f(a)f(b)) f(H) = (f(a)f(H))(f(b)f(H)) = eta(a H)eta(b H)`. 因此 `eta` 为一同构映射.

商群同构定理 令 `G` 为一群, `K, H normal G`, `K le H`. 则 `G//H ~= (G//K)//(H//K)`.

由条件知 `K normal H`. 取满同态 `f: g in G to g K in G//K`, 则 `"Ker"f = f^-1(e K) = K sube H`. 应用第一同构定理即得结论.

设群 `K, H normal G`, `K le H`, 则 `H//K = G//K iff H = G`.

第二同构定理 令 `G` 为一群, `H normal G`, `K le G`. 则 `K H//H ~= K//(K nn H)`.

易知 `K nn H normal K nn G = K`, `K H le G`. 显然 `H le K H`, 从而由 `H normal G` 知 `H normal K H`.

`AA k in K, h in H`, `(k h) H = k (h H) = k H`. 作 `f: k H in K H//H to k(K nn H) in K//(K nn H)`. 由 `k_1 H = k_2 H` `iff k_1^-1 k_2 in H` `iff k_1^-1 k_2 in H nn K` `iff k_1 (H nn K) = k_2 (H nn K)` 知, `f` 为一映射, 且为一单射. 显然 `f` 为一满射, 从而 `f` 为一双射. 又 `f(k_1 H k_2 H) = f(k_1 k_2 H) = k_1 k_2 (K nn H)` `= k_1(K nn H) k_2 (K nn H) = f(k_1 H) f(k_2 H)`, 故 `f` 为一同态映射, 从而 `f` 为一同构映射.

作满同态 `varphi: k in K to k H in K H // H`, 又 `AA k in K`, `k in "Ker"varphi iff k H = H` `iff k in H iff k in H nn H`, 从而 `"Ker"varphi = K nn H`. 于是由同态基本定理即得结论.

群的直积 (direct product)

[来自 小时百科]

外直积

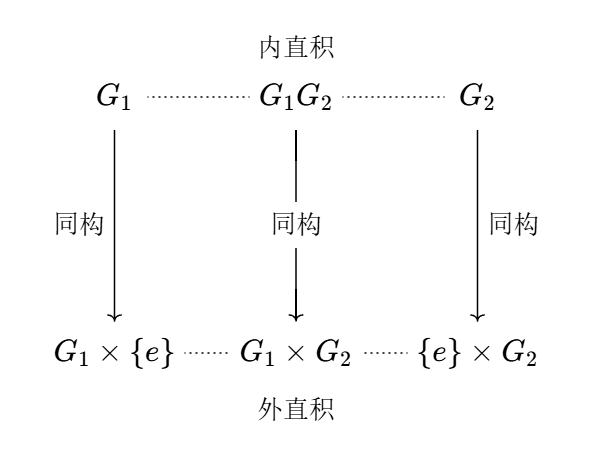
令 `G_1`, `G_2` 为两个群, 考虑集合笛卡尔积 `G_1 xx G_2` 上的二元合成: `(a, b) * (c, d) := (a c, b d)`, (对应分量相乘) 可以验证 `(G_1 xx G_2, *)` 成一群. 因为它是从两个较小的群组合而来, 称其为群 `G_1, G_2` 的外直积 (external direct product).

群到外直积的嵌入 `G_1 ~= G_1 xx {e_2} := {(a, e_2) | a in G_1}`,
`G_2 ~= {e_1} xx G_2 := {(e_1, b) | b in G_2}`, 其中 `e_1, e_2` 分别为群 `G_1, G_2` 的幺元. 上式右边的群是 `G_1 xx G_2` 的正规子群.

只证第一式. 作 `varphi: g mapsto (g, e_2)`, 显然 `varphi` 为一双射. 又 `AA g, h in G_1`, `varphi(g h) = (g h, e_2) = (g, e_2) (h, e_2) = varphi(g) varphi(h)`. 从而 `varphi` 为一同态. 因此 `varphi` 是同构映射.
下面验证 `G_1 xx {e_2} normal G_1 xx G_2`. 这是因为 `(g_1, g_2)(a, e_2)(g_1, g_2)^-1` `= (g_1 a g_1^-1, e_2)` `in G_1 xx {e_2}`.

我们看到 `G_1 xx {e}` 和 `{e} xx G_2` 是 `G_1 xx G_2` 的正规子群, 且 `G_1 xx G_2` 的每个元素都能唯一地写为两个正规子群的元素乘积: 这引出下节的内直积定义.

内直积

设群 `G` 的子群 `G_1, G_2` 满足:
1. `G_1, G_2 normal G`;
2. `G = G_1 G_2`;
3. `G_1 nn G_2 = {e}`;
则称 `G` 是 `G_1, G_2` 的内直积 (internal direct product). 相比于外直积, 这里 `G` 是事先给定的群, 满足一定的内部构造.

1. `G_1 xx G_2` 是 `G_1 xx {e}` 和 `{e} xx G_2` 的内直积.
2. 线性空间 (看作加法群) 的直和是内直积.

回忆线性空间直和的等价条件, 立即得到:

内直积的等价条件 内直积定义的第 3 条可以换成以下任一条:
1. `G` 的任一元素表为 `G_1, G_2` 中元素乘积的方式惟一;
2. `G` 中存在一元素, 表为 `G_1, G_2` 中元素乘积的方式惟一;
3. `G` 的幺元表为 `G_1, G_2` 中元素乘积的方式是惟一的, 即 `e = e e`;
4. `G_1 nn G_2 = {e}`;

1. `rArr` 2. 显然.
2. `rArr` 3. 设 `g = g_1 g_2` 是元素 `g in G` 的惟一分解, 其中 `g_1 in G_1`, `g_2 in G_2`. 设 `e = a b`, 其中 `a in G_1`, `b in G_2`, 则 `g = g_1 g_2 e = g_1 g_2 a b = g_1 (g_2 a g_2^-1) g_2 b`, 其中 `g_1 (g_2 a g_2^-1) in G_1`, `g_2 b in G_2`. 由 `g = g_1 g_2` 是惟一分解知 `g_1(g_2 a g_2^-1) = g_1`, `g_2 b = g_2`. 从而 `a = b = e`.
3. `rArr` 4. 若 `g in G_1 nn G_2`, 由 `G_1 nn G_2 le G` 知 `g^-1 in G_1 nn G_2`, 于是 `e = g g^-1`. 但 `e = e e` 是幺元的惟一分解, 所以 `g = e`.
4. `rArr` 1. 设存在元素 `g = g_1 g_2 = h_1 h_2`, 其中 `g_1, h_1 in G_1`, `g_2, h_2 in G_2`. 则 `h_1^-1 g_1 = h_2 g_2^-1 in G_1 nn G_2`, 由 `G_1 nn G_2 = {e}` 知, `h_1 = g_1`, `h_2 = g_2`.
注意以上证明只有 2. `rArr` 3. 用到了子群 `G_1` 的正规性.

我们打算证明内直积和外直积同构, 将过程拆解为下面的引理:

令 `G_1, G_2 normal G`, `G_1 nn G_2 = {e}` 则 `G_1, G_2` 之间元素的乘积可交换, 即 `(AA g_1 in G_1, g_2 in G_2)` `g_1 g_2 = g_2 g_1`.

(利用换位子的概念) `AA g_1 in G_1, g_2 in G_2`, 由 `G_1, G_2 normal G` 知 `g_1 g_2 g_1^-1 g_2^-1 = g_1 (g_2 g_1^-1 g_2^-1) in G_1`,
`g_1 g_2 g_1^-1 g_2^-1 = (g_1 g_2 g_1^-1) g_2^-1 in G_2`. 从而 `g_1 g_2 g_1^-1 g_2^-1 in G_1 nn G_2 = {e}`, 即 `g_1 g_2 = g_2 g_1`.

[来自群友 幂零群] 设 `G_1, G_2 le G`, 定义乘法映射 `varphi: (g_1, g_2) in G_1 xx G_2 mapsto g_1 g_2 in G`. 则
1. `varphi` 是同态当且仅当 `G_1, G_2` 的元素可交换.
2. 在 1. 的基础上, `varphi` 升级为同构当且仅当 `G_1 nn G_2 = {e}` 且 `G_1 G_2 = G`.

1. `varphi` 是同态等价于 `(AA g_1, h_1 in G_1, g_2, h_2 in G_2)` `varphi(g_1, g_2) varphi(h_1, h_2) = varphi(g_1 h_1, g_2 h_2)`
   `iff (AA g_1, h_1 in G_1, g_2, h_2 in G_2)` `g_1 g_2 h_1 h_2 -= g_1 h_1 g_2 h_2`
   `iff (AA h_1 in G_1, g_2 in G_2)` `g_2 h_1 -= h_1 g_2`.
2. `varphi` 是满射 `iff G` 中元素总能表为 `G_1, G_2` 元素的乘积 `iff G_1 G_2 = G`.
   `varphi` 是单射 `iff G` 中元素表为 `G_1, G_2` 元素乘积的方式唯一 `iff G_1 nn G_2 = {e}`.

---

[注] 满射 `iff` 原像的存在性; 单射 `iff` 原像的唯一性.

群的直积分解定理 (内外直积的等价性)
1. `G_1 xx G_2` 是 `G_1 xx {e} ~= G_1` 和 `{e} xx G_2 ~= G_2` 的内直积;
2. 反之, 设 `G` 是 `G_1, G_2` 的内直积, 则 `G ~= G_1 xx G_2`.
如下图, 其中虚线 `A cdots B cdots C` 表示中间的群 `B` 是 `A, C` 的内直积.

结论 1. 已在定义内直积时给出. 至于 2., 由于 `G_1, G_2 normal G`, `G_1 G_2 = G` 和 `G_1 nn G_2 = {e}` 三个条件同时满足, 由引理知道乘法映射 `varphi: (g_1, g_2) mapsto g_1 g_2` 是同构.

此定理表明, 内、外直积是同构的, 我们统称为直积 (direct product). 特别当 `G_1, G_2` 为 Abel 群时, `G_1 xx G_2` 也为 Abel 群, 称为 `G_1, G_2` 的直和 (direct sum) `G_1 o+ G_2`. 直积的概念容易推广到多个群的情形.

半直积

[来自 sola@知乎]

将内直积定义中的其中一个正规子群减弱为子群, 定义半直积 (semi-direct product)如下:

半直积 (内) 令 `G` 为一群, `N normal G`, `H le G`, 且 `G = N H`. 若 `N nn H = {e}`, 则称 `G` 是 `N` 和 `H` 的半直积, 记为 `G = N ><| H`.

1. `C_6 ~= C_3 xx C_2`, `D_6 ~= C_3 ><| C_2`. 其中 `C_3` 是正规子群.
2. `RR^n` 上的刚体变换群 `M_n` 是平移变换群 `T_n` 与正交变换群 `O_n` 的半直积: `M_n = T_n ><| O_n`.

记号 `N ><| H` 中哪个群是正规的? 是 “又”的两条腿指向的那个.

半直积的另一定义不依赖于预先给定的群 `G`, 这个定义稍显复杂:

半直积 (外) 给定群 `N, H` 和同态 `f: H to "Aut"N`. 对于任意 `h in H`, `f_h := f(h)` 是一个 `N to N` 的同构映射. 现在集合 `N xx H` 上定义运算 `(*)`: `(n_1, h_1) * (n_2, h_2) := (n_1 * f_(h_1)(n_2), h_1 * h_2)`, 则 `(N xx H, *)`, 为一群, 记为 `N ><|_f H`.

[来自群友 幂零群] 形式地记 `[1; n, h] := (n, h)`, 则半直积的乘法可以用矩阵乘法帮助记忆: `[1; n_1, h_1] [1; n_2, h_2]` `= [1; n_1 + h_1 n_2, h_1 h_2]`.

在半直积群 `N ><|_f H` 中, `(n, h)^-1 = (f_(h^-1)(n^-1), h^-1)`.

`(n, h)(f_(h^-1)(n^-1), h^-1)` `= (n * f_(h)(f_(h^-1)(n^-1)), e)` `= (n * n^-1, e)` `= (e, e)`.

当同态 `f = "id"` (恒等映射) 时, 半直积退化为直积. 反之, 若 `f` 非平凡, 则 `N ><|_f H` 是非交换群.

半直积分解 验证半直积两个定义的等价性.

1. `rArr` 2. 设 `N normal G`, `H le G`, `G = N H`, `N nn H = {e}`. 取同态 (它将 `h` 映到 `N` 上的内自同构): `f := h mapsto n mapsto h n h^-1`, 作 `varphi: (n, h) in N xx H mapsto n h in G`, 然后验证它是同构即可. 事实上, `G = N H` 保证它是满的, `N nn H = {e}` 保证它的核是 `{e}`. 再验证它是同态: `varphi(n_1, h_1) varphi(n_2, h_2)` `= n_1 h_1 n_2 h_2` `= n_1 f_(h_1)(n_2) h_1 h_2` `= varphi((n_1, h_1) * (n_2, h_2))`.
2. `rArr` 1. 将 `N` 与 `{(n, e): n in N}` 等同, `H` 与 `{(e, h): h in H}` 等同, 则 `N, H` 是 `N xx H` 的子群. 又 `AA (n_1, h) in N xx H, (n_2, e) in N`, `(n_1, h) (n_2, e) (n_1, h)^-1 = (..., e) in N`, 所以 `N normal N xx H`. 一方面, 显然有 `N xx H supe N H`; 另一方面, `AA (n, h) in N xx H`, `(n, e) xx (e, h) = (n * f_e(e), h) = (n, h)`, 所以 `N xx H sube N H`, 于是 `N xx H = N H`. 最后, 显然 `N nn H = {(e, e)}`, 所以 `N xx H` 是一个半直积.

半直积仍然不能确定群的同构类, 这意味两个不同构的群可以有完全相同的 (半) 直积分解. 为了找到 `N ><| H` 的所有同构类, 我们必须讨论 `H to "Aut" N` 的所有可能同态. 利用半直积可以处理如 `2p` 阶群、12 阶群的分类问题, 但仍有一些问题是困难的, 例如 `2^n` 阶群的分类问题. 与其他有限群相比, `2^n` 阶群的同构类特别多. 例如 64 阶群有 267 种, 128 阶群多达 2328 种, 参见 Finite Group - Wolfram Math World.

下面两个命题常常是寻找半直积的着手点:

子群乘积的阶数公式 `G` 为有限群, `H, K le G`, 则 `|H K| = (|H| |K|)/|H nn K|`. 注意 `H K` 未必是子群, 除非 `H K = K H`.

见 习题 21.

`G` 为有限群, `H, K` 是两个阶数互素的子群, 则 `H nn K = {e}`; 进一步若 `|H| |K| = |G|`, 则 `H K = G`.

1. 由 Lagrange 定理知道, 子群元素的阶整除子群的阶, 但 `|H|, |K|` 互素, 所以它们只有平凡交.
2. 由 1. 和阶数公式知道 `|H K| = |G|`.

积与商的关系

商群的直积 设群 `N_1 normal G_1`, `N_2 normal G_2`, 则 `N_1 xx N_2 normal G_1 xx G_2`, 且 `(G_1 xx G_2) // (N_1 xx N_2) ~= G_1//N_1 xx G_2 // N_2`.

自由群

群展示 (presentation) 是群的一种记号, 把群的生成元写在左边, 生成关系写在右边, 例如
1. `n` 阶循环群记为 `(:a | a^n = 1:)`.
2. `K_4` 记为 `(:a, b | a^2 = 1, b^2 = 1, a b = b a:)`.
同一个群往往有不同的展示. 比如 `K_4` 还可以写为 `(:a, b | a^2 = 1, b^2 = 1, (a b)^2 = 1:)`. 我们常常省略群展示中的 "`=1`", 比如 `K_4` 的第一种写法可以简记为 `(:a, b | a^2, b^2, a b a^-1 b^-1 :)`.

from sympy.combinatorics.free_groups import free_group
from sympy.combinatorics.fp_groups import FpGroup
F, a, b = free_group('a, b')
G = FpGroup(F, [a**2, b**2, a*b*a**-1*b**-1])
G.is_abelian # True
G.order() # 4

自由乘积 令 `A, B` 是两个群, `A ⊔ B` 是它们的无交并. 定义它们的自由乘积为如下集合: `A ast B := { prod_(i=1)^n x_i: x_i in A ⊔ B }` 其中每个乘积 `prod x_i` 都只有有限项. 我们希望 `A ast B` 是一个群, 可作如下规定:
• 当 `n = 0` 时, 记 `prod_(i=1)^0 x_i = 1` 是新群的单位元.
• `n gt 0` 时, 规定乘积当中不含 `A` 或 `B` 的单位元, 且任意相邻两项不属于同一个群 (否则可以将它们相乘, 得到一个更简短的乘积).
• 对任意 `x_1 cdots x_n in A`, `y_1 cdots y_m in B`, 定义它们的乘积为两个乘积的简单拼接: `x_1 cdots x_n * y_1 cdots y_m`. 假如拼接后的乘积含有单位元, 或者有相邻两项属于同一个群, 就对它们进行简化, 得到一个最简的乘积为止.
可以证明, `A ast B` 关于上述乘法构成一个群. 一般地, 对一族群 `{G_lambda}_(lambda in Lambda)`, 也可以定义自由乘积 `prod_(lambda in Lambda)^ast G_lambda := { prod_(i=1)^n x_i: x_i in ⨆_(lambda in Lambda) G_lambda }`. 同样规定每个有限乘积中不含单位元, 且相邻两项不属于同一个群.

两个元素生成的有限群 (其中一个生成正规子群) [来自群友 问情明心] 令 `G` 是有限群.
1. 设元素 `a in G` 生成的 `m` 阶循环群 `(:a:)` 是 `G` 的正规子群, 且商群 `G // (:a:)` 是 `n` 阶循环群. 取商群的一个生成元 `b (:a:)`, 证明: `G` 为 `m n` 阶有限群, 且满足下面的生成关系 `G = (: a, b | a^m = 1, b^n = a^r, b a b^-1 = a^s :)`, (`ast`) 其中 `r, s in ZZ`, 且 `r(s-1)` 和 `s^n - 1` 都是 `m` 的倍数.
2. 反之, 设 `G(m, n, r, s)` 由 (`ast`) 的关系生成, 其中 `m, n in ZZ_(ge 0)`, `r, s in ZZ`, 且 `m`, `r(s-1)`, `s^n - 1` 不全为零. 证明: `G` 是 `q n` 阶有限群, 其中 `q = gcd(m, r(s-1), s^n - 1)`. 其中 `(:a:)` 是 `G` 的 `q` 阶正规子群, 且商群 `G // (:a:)` 是 `n` 阶循环群.
3. 我们列出几个特例:
   • `s -= 1 (mod m)` 时, `b a = a b`, `G` 为 Abel 群, `G ~= (:a:) xx (:b:)`.
   • `r = 0` 时, `b^n = 1`, 可以验证 `G ~= (:a:) ><| (:b:)`. 特别取 `G(m, n = 2, r = 0, s = -1)` 就得到二面体群 `D_(2m)`.
   • `G(2n, 2, n, -1)` 称为双循环群 (dicyclic group) `"Dic"_(4n)`. 特别 `G(4, 2, 2, -1)` 称为四元数群 `Q_8`.

1. 由 Lagrange 定理知道 `G` 的阶数是 `m n`. 每个 `g in G` 都可以写成 `a^x b^y`. 这是因为 `b (:a:) = (:a:) b` 是商群的生成元从而存在 `y` 使得 `(:a:) g = (:a:) b^y`, 于是存在 `x` 使得 `g = a^x b^y`.
   由商群的阶为 `n` 知道 `b^n (:a:) = (:a:)`, 即 `b^n in (:a:)`. 于是可记 `b^n = a^r`. 又由 `(:a:)` 是正规子群知道 `b a b^-1 in (:a:)`, 于是可记 `b a b^-1 = a^s`. 下证 `m` 整除 `r(s-1)` 和 `s^n-1`, 这只需证 `a` 的对应次方等于 `1`: `a^(r(s-1))` `= a^(s r) a^-r` `= b a^r b^-1 a^-r` `= b^0` `= 1`,
   `a^(s^n-1)` `= a^(s^n) a^-1` `= b a^(s^(n-1)) b^-1 a^-1` `= b^n a b^-n a^-1` `= a^0` `= 1`.
2. 设 `|a| = q`, 下证 `q = gcd(m, r(s-1), s^n - 1)`. 由 1. 知, `G` 的生成关系可以改写为 (??) `G = (: a, b | a^m = 1, b^n = a^r, b a b^-1 = a^s, a^(r(s-1)) = a^(s^n-1) = 1 :)`, 所以 `q` 是这三个数的公约数.
   下证 `(:a:)` 是正规子群. 利用关系 `b a b^-1 = a^s` 即 `b a = a^s b`, 可以把 `G` 中的元素都写成 `a^x b^y` 的形式. 对任意 `g = a^x b^y in G`, `g (:a:) g^-1` `= a^x b^y (:a:) b^-y a^-x` `= a^x (:a:) b^y b^-y a^-x` `in (:a:)`. 因此 `(:a:) normal G`.
   [来自群友 幂零群] 下证 `G//(:a:)` 是 `n` 阶循环群. `G//(:a:)` 相当于在 `G` 的生成关系中添加一条 `a = 1` (??), 于是 `G//(:a:) = (: a, b | a = 1, b^n = 1 :)`, 这就是 `n` 阶循环群.

四元数群 记 `i = a`, `j = b`, `k = i j`, 由上例知道 `Q_8 = (:i, j | i^4 = 1, j^2 = i^2, j i j^-1 = i^-1 :)`. 第三个等式改写为 `i j i = j` 即 `i j i j = j^2`, 即 `i j k = k^2 = j^2 = i^2`. 记 `i^2 = m`, 则 `m` 是 `Q_8` 的唯一 2 阶元. `Q_8` 的全体元素为 `{1, m, i^(+-1), j^(+-1), k^(+-1)}`. 除了 `1, m` 以外, 其余元素的阶数都是 4.
`Q_8` 是非交换群, 但它的每个子群都正规: 2 阶子群只有 `{1, m}`, 它是 `Q_8` 的中心. 4 阶子群在 `Q_8` 中的指数是 2 因此必正规.

有限生成 Abel 群

1 到 15 阶群的分类

[来自 知乎@格罗卜学数学]

1. 有限阶交换群可以分解为循环群的直积; 若 `p, q` 互素, 则 `C_p xx C_q ~= C_(p q)`, 因此不妨令这些循环群的阶两两不互素.
2. `n ge 3` 时, `S_n` 是非交换群;
3. `n ge 6` 时, `D_n := (: x, y | x^n = e, y^2 = e, x y x y = e :)` 是非交换群;
4. 双循环群 (dicyclic group) `"Dic"_(4n) := (: x, y | x^(2n) = e, y^2 = x^n, y x y^-1 = x^-1 :)` 特别 `Q_8 := "Dic"_8` 是四元数群. 双循环群由两个元素生成.

处理小阶群时有用的结论

关于 2 阶元:
1. 群 `G` 中除 `e` 外元素阶全为 2, 则 `G` 是交换群;
2. 偶数阶群必有奇数个 2 阶元;
3. 群 `G` 不能只有两个 2 阶元.

例如 `K_4` 由单位元 `e` 和 3 个 2 阶元组成, 满足 1. 的条件, 是交换群. `K_4` 是偶数阶群, 满足 2. 的条件: 而它确有奇数个 2 阶元. 群 `G` 不能只有两个 2 阶元. 如 `C_4` 有 1 个 2 阶元, 而 `K_4` 有 3 个.

1. 在 `x y x y = e` 左边乘以 `x`, 右边乘以 `y`.
2. 设元素 `a` 的阶 `gt 2`, 则 `a^-1 != a`, 这说明 `G` 中阶大于 2 的元素 (如果存在) 是成对出现的. 又 `G` 的 1 阶元只有单位元 `e`, 所以 `G` 的 2 阶元数目为奇数个.
3. 假设 `G` 只有两个 2 阶元 `x != y`.
   1. 考虑元素 `x y`. 我们有 `x y != x x = e`,
      `x y != x e = x`,
      `x y != e y = y`. 因此 `x y` 是不同于 `e, x, y` 的一个新元素.
   2. 考虑元素 `x y x`. 我们有 `x y x != x e x = e`,
      `x y x != x x x = x`,
      `x y x != y`, 否则 `x y x y = y y = e`, 这推出 `x y` 是二阶元. 因此 `x y x` 也是一个不同于 `e, x, y` 的新元素.
   3. 计算 `(x y x)(x y x) = (x y)(y x) = x x = e`, 因此 `x y x` 是二阶元. 矛盾.

指数与正规子群: 若 `G` 的子群 `H` 的指数为 `p`, 这里 `p` 是 `|G|` 的最小素因子, 那么 `H normal G`. 特别地, 指数为 2 的子群必为正规子群.

设 `p` 为素数:
1. `p` 阶群只有一种, 那就是循环群;
2. `2p` 阶群只有两种, `C_(2p)` 和 `D_(2p)`;
3. `p^2` 阶群只有两种, `C_(p^2)` 和 `C_p xx C_p`;

1. 由 Lagrange 定理, `p` 阶群的 `G` 的子群阶数只能为 `1` 或 `p`, 从而元素的阶也只能为 `1` 或 `p`. 其中的 `p` 阶元素生成了整个群 `G`, 所以 `G` 是循环群.
2. 和 3. 的证明见下一章, 我们将用 Sylow 定理对 `p q` 阶群 (`p, q` 为素数) 进行分类.