[来自 知乎@ZCC, 知乎@0003 ]

  1. 没有特别说明时, 本章涉及的环均为交换幺环.
  2. 模是一种重要的代数结构, 可以类比于线性空间. 与线性空间不同的是, 其中的标量不再属于一个域, 而是在一个交换幺环中, 而环中的元素未必有逆. 这造成了模与线性空间的各种不同, 学习时需加以留意.
  3. 模论是交换代数、群表示论和同调代数的基础. 对于想快速入门域论和 Galois 理论的同学, 看完模与代数的定义就可以前往下一章了😄
    4. 简言之, 模是在环与 Abel 群间定义了一种数乘, 而代数是模上定义了一个双线性映射.

模

模 (module) 设 `R` 为幺环[], `(M, +)` 是 Abel 群, 给定映射 `f: R xx M to M`
`(a, x) mapsto a x` 满足 `AA a, b in R`, `x, y in M`, `a(x + y) = a x + a y`,
`(a + b) x = a x + b x`,
`(a b) x = a (b x)`,
`1_R x = x` 则称 `f` 是一个数乘或标量乘法, `M` 是 `R` 上的一个左模, 或简称左 `R`-模. 把以上定义的左乘全部改为右乘, 则可以定义右 `R`-模.

[来自群友 西伯利亚的猫猫] 不含幺元的环, 应该叫「坏」吧.

左模与右模除了乘法的次序不同外, 性质没有任何区别. 特别当 `R` 为交换幺环时, 左模与右模没有区别. 下文内容如不加说明都指左模.

  1. 域 `bbb F` 上的模其实就是线性空间.
  2. 零模: 只含零元素的模.
  3. `ZZ`-模: 设 `M` 为 Abel 群, 定义映射 `ZZ xx M to M` 使得 `(n, x) mapsto n x`, 其中 `n x` 就是 `n` 个 `x` 之和, 则 `M` 是一个 `ZZ`-模. 任意交换群都可以看作是一个 `ZZ`-模.
  4. 自同态模: 设 `M` 为 Abel 群, `"End"(M)` 为它的自同态环, 其中乘法定义为 `(sigma * tau)(x) = sigma(tau(x))`, 加法为 `(sigma + tau)(x) = sigma(x) + tau(x)`. 给定映射 `"End"(M) xx M to M` 使得 `(sigma, x) mapsto sigma(x)`, 则 `M` 是 `"End"(M)` 上的模.
  1. 子模: 若 `M` 是 `R`-模, `N` 是 `M` 的子群, 且对数乘封闭: `AA a in R, y in N` 有 `a y in N`, 则称 `N` 是 `M` 的子模.
  2. 商模: 设 `M` 是 `R`-模, `N` 是 `M` 的子模, 定义 `R` 与商群 `M // N` 之间的数乘 `R xx M // N to M // N`
    `(a, x + N) mapsto a x + N`,     则 `M//N` 是 `R`-模, 称为 `M` 关于 `N` 的商模.
  3. 同态: 若 `M, N` 是 `R`-模, `f: M to N` 是 Abel 群的同态, 且满足 `AA a in R`, `x in M`, `f(a x) = a f(x)`, 则称 `f` 是 `M` 到 `N` 的 `R`-模同态, 简称模同态.

代数

    代数 (algebra) 设 `R` 为交换幺环, `M` 是 `R` 上的左模, `(*)` 是 `R`-双线性映射, 即 `AA a, b in R`, `x, y, z in M`, `(a x + b y) * z = a (x * z) + b (y * z)`,
    `z * (a x + b y) = a (z * x) + b (z * y)`.     则称 `(*)` 是 `M` 上的乘法, `(M, *)` 是 `R` 上的一个代数, 或简称 `R`-代数.
  1. 同态: 若 `M`, `N` 是 `R`-代数, `f: M to N` 是 `R`-模同态, 且满足 `AA x, y in M`, `f(x * y) = f(x) * f(y)`, 则称 `f` 是 `M` 到 `N` 的 `R`-代数同态.
  2. 结合、交换、含幺、可除: 若 `M` 上的乘法满足结合律/交换律/有幺元/无零因子, 则分别称代数 `M` 是结合的/交换的/含幺的/可除的. 其中幺元指 `x 1 = 1 x = x`, 无零因子指 `x y = 0 rArr x = 0 or y = 0`.
  1. `R` 自身是一个 `R`-代数.
  2. 自同态代数: `R`-模 `M` 的全体自同态 `"End"(M)` 关于映射的复合构成一个 `R`-代数.
  3. 矩阵代数: 环 `R` 上的 `n` 阶矩阵环 `M_n(R)` 关于矩阵乘法构成一个 `R`-代数.
  4. 李代数: `bbb F`-线性空间 `fr g` 关于其上的 Lie 括积运算构成一个 `bbb F`-代数. 所谓 Lie 括积是指一个双线性映射 `[*,*]`, 满足 `AA x, y, z in fr g`, `[x, x] = 0`,
    `[x, [y, z]] + [y, [z, x]] + [z, [x, y]] = 0`.

可除代数

  1. 四元数: `bbb H = "span"{1, i, j, k}` 是 `RR` 上的 4 维可除代数, 满足 `i^2 = j^2 = k^2 = i j k = -1`. 在 `i j k = -1` 等号两边右乘 `k` 得 `i j k^2 = -k`, 即 `i j = k`. 同理 `j k = i`, `k i = j`. 四元数乘法不满足交换律.
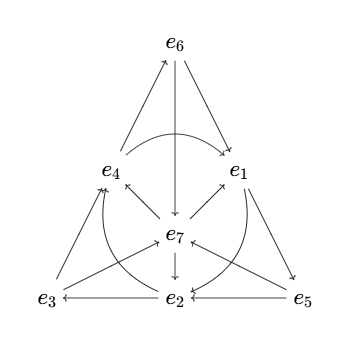
  2. [来自 法会因由@知乎] 八元数: `bbb O = "span"{1, e_1, cdots, e_7}` 是 `RR` 上的 8 维可除代数. 它的运算法则可以用 Fano 平面 `PG(2,2)` 来记忆: Fano 平面有 7 个点和 7 条边, 每条边上有 3 个点, 每个点是 3 条边的交点. 顺着箭头方向: `e_1 e_2 = e_4`; 逆着箭头方向: `e_2 e_1 = -e_4`.
    1. `e_i^2 = 1`, `e_i e_j = e_k = -e_j e_i`;
    2. 指标循环: `e_i e_j = e_k` `rArr e_(i+1) e_(j+1) = e_(k+1)`;
    3. 指标翻倍: `e_i e_j = e_k` `rArr e_(2i) e_(2j) = e_(2k)`;
    4. 不满足结合律: `e_1 (e_2 e_3) = e_6`, `(e_1 e_2) e_3 = -e_6`.

若代数 `M` 上配备了一个内积 `(*,*)` 使得 `(x y, x y) = (x, x) (y, x)`, 就称 `M` 是赋范的. 设 `M` 是一个赋范可除代数, `x, y` 的实部为零, 它们的叉积定义为相乘取虚部: `x xx y` `:= "Im"(x y)` `= 1/2 (x y - y x)`. `= 1/2 [x, y]`.

外代数

    设 `V` 是域 `bbb F` 上的线性空间. 规定楔积运算 `^^` 满足如下性质:
  1. 双线性性: `AA a, b in bbb F`, `AA x, y, z in V`, `(a x + b y) ^^ z = a (x^^z) + b (y^^z)`,
    `z ^^ (a x + b y) = a (z^^x) + b (z^^y)`.     因此 `{:^^:}^2 V := { sum x ^^ y: x, y in V }` 构成线性空间.
  2. 反对称性: `x ^^ y = 0 iff x = y`.
    因为 `^^` 是双线性的, 我们有 `0 = (x+y) ^^ (x+y)` `= x ^^ x + y ^^ y + x ^^ y + y ^^ x`, 即 `x ^^ y = -y ^^ x`.
  3. 结合性: 规定 `V` 中元素和 `^^ ^2 V` 中元素也可以进行 `^^` 运算, 且 `AA x, y, z in V`, `(x ^^ y) ^^ z = x ^^ (y ^^ z)`; 因此 `^^ ^3 V := { sum x ^^ y ^^ z: x, y, z in V }` 也构成线性空间. 一般地, 可以构造出线性空间 `^^ ^k V := { sum x_1 ^^ cdots ^^ x_k: x_i in V, i = 1, cdots, k }`.
  4. 特别地, 记 `^^ ^0 V := bbb F`, `^^ ^1 V := V`.
    5. 由于 `V` 中两元素相乘得到的是 `V` 之外的元素, 我们称 `(V, ^^)` 为外代数 (exterior algebra) 或 Grassmann 代数.
    维数公式 设 `V` 为有限维, `{e_i}_(i=1)^n` 是 `V` 的基, 则
  1. `^^ ^k V` 的基由 `k` 个基向量外积得到, 维数为 `C_n^k`. 比如 `n = 3` 时, `^^ ^2 V` 的基为 `{e_1 ^^ e_2, e_2 ^^ e_3, e_3 ^^ e_1}`.
  2. `k gt n = dim V` 时, `^^ ^k V = {0}`.
  3. 将所有 `^^ ^k V` 做直和得到外积空间 `^^ V := o+_(k=0)^n ^^ ^k V`, 维数为 `sum_(k=0)^n C_n^k = 2^n`.
  1. `RR^3` 中的叉乘 注意到 `dim R^3 = dim ^^ ^2 RR^3`, 给定 `RR^3` 的标准正交基 `{i, j, k}`, 可以建立同构 `varphi`, 使得 `varphi(i ^^ j) = k`, `varphi(j ^^ k) = i`, `varphi(k ^^ i) = j`.
  2. `RR^7` 中的叉乘 [来自 知乎] `n` 维空间的一组单位正交基记为 `bm e_1, cdots, bm e_n`. 其中叉乘应该满足:
    1. `bm e_i xx bm e_i = bm 0`;
    2. `bm e_i xx bm e_j = -bm e_j xx bm e_i`;
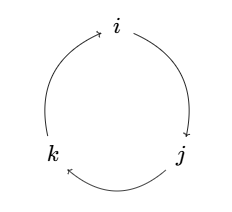
    3. `i != j` 时, 存在一个与 `i, j` 都不同的 `k`, 使得 `bm e_i xx bm e_j = +-bm e_k`, `quad bm e_j xx bm e_k = +- bm e_i`, `quad bm e_k xx bm e_i = +- bm e_j`. 以上三个等式要么同时取正号, 要么同时取负号. 形象地说, `bm e_i, bm e_j, bm e_k` 在叉乘下形成一个三角形.
    现在假定 `n gt 3`, 且 `bm e_1 xx bm e_2 = bm e_3`.
    考虑另一个基矢量 `bm e_4`, 由于 `bm e_1, bm e_2, bm e_3` 已经形成三角形, 所以 `bm e_1 xx bm e_4` 不能等于 `+- bm e_i`, `i = 1, 2, 3, 4`. 我们设 `bm e_1 xx bm e_4 = bm e_5`. 于是 `bm e_1, bm e_4, bm e_5` 形成一个三角形. 同理 `bm e_2 xx bm e_4` 不能等于 `+- bm e_i`, `i = 1, 2, 3, 4, 5`. 设它等于 `bm e_6`. `bm e_3 xx bm e_4` 不能等于 `+- bm e_i`, `i = 1, 2, 3, 4, 5, 6`. 设它等于 `bm e_7`. 至此我们证明了 4 到 6 维空间不能定义叉乘. 但 7 维空间的确存在一个叉乘. 见下表, 上面的推理可以总结为表格中的黑色文字, 但蓝色文字还未填出. 考虑 `bm e_1 xx bm e_6`. 排除掉同一行的 3, 2, 5, 4, 以及自身的 1, 6, 我们发现必有 `bm e_1 xx bm e_6 = +- bm e_7`. 同理 `bm e_2 xx bm e_7 = +- bm e_5`, `bm e_3 xx bm e_6 = +- bm e_5`. 这三个等式都取正号的话, 就得到下表:
    `xx` 1 2 3 4 5 6 7
    1 0 3 -2 5 -4 7 -6
    2 0 1 6 -7 -4 5
    3 0 7 -6 5 -4
    4 0 1 2 3
    5 0 -3 -2
    6 0 1
    7 0