这里将要研究的是 2 维以及 3 维 Euclid 空间 `E^2` 与 `E^3`, 通过向量的概念及其性质, 以及高等代数中关于向量空间的结论, 首先建立几何空间的仿射坐标系, 刻画其线性结构 (基, 线性相关, 线性无关); 既而, 运用向量的内积与外积, 刻画其度量结构 (角度, 距离, 面积, 体积).

向量及其线性运算

基本概念

既有大小, 又有方向的量称为向量或矢量, 用符号 `bm a, bm b, bm c, cdots` 或 `vec a, vec b, vec c` 表示.

向量 `bm a` 可以用一条有向线段 `vec(AB)` 表示, 用其长度 `|AB|` 表示向量的大小, 用 `A` 到 `B` 的指向表示向量的方向, 记为 `vec(AB) = bm a`. 不过向量不等同于有向线段, 它仅仅是 "大小" 与 "方向" 两个概念的集合, 即, 如果两个向量的大小与方向都相等, 则它们是同一向量. 因此, 若把 `vec(AB)` 平行移动, 得到的有向线段 `vec(CD)` 仍表示同一向量. 记 `vec(AB) = vec(CD)`.

向量 `bm a` 的大小又称为长度或模, 记为 `|bm a|`. 称长度为 0 的向量为零向量, 记为 `bb 0`. 零向量的方向不确定: 我们规定它与任意向量都是同向的. 称长度为 1 的向量为单位向量. 称长度与 `bm a` 相等, 方向与 `bm a` 相反的向量为 `bm a` 的反向量, 记为 `-bm a`. 例如, `vec(BA) = -vec(AB)`.

我们考虑的向量总是属于某一集合的. 比如, 属于 2 维或 3 维 Euclid 空间 (`E^2` 或 `E^3`). 这一集合称为向量空间. 下面将引出向量的两种线性运算——加法与数乘, 联系高等代数的知识可以知道, 向量空间是典型的线性空间.

向量的加法

三角形法则 设有向量 `bm a, bm b`, 选择一起点 `A`, 作有向线段 `vec(AB) = bm a`, `vec(BC) = bm b`, 则称 `vec(AC)` 表示的向量为 `bm a` 与 `bm b` 的和, 即 `vec(AB) + vec(BC) = vec(AC)`.

若另取一个起点 `A_1`, 作 `vec(A_1 B_1) = bm a`, `vec(B_1 C_1) = bm b`, 容易说明 `vec(A_1 C_1)` 与 `vec(AC)` 表示同一个向量. 因此向量的加法与起点选择无关.

也可以选取起点 `O`, 作 `vec(OA) = bm a`, `vec(OB) = bm b`, 再以 `OA` 和 `OB` 为邻边作平行四边形 `OACB`. 容易说明对角线 `vec(OC) = bm a + bm b`. 这称为向量加法的平行四边形法则.

向量加法的性质 设 `bm a, bm b, bm c` 是任意向量, 则它们满足
1. 结合律. `(bm a + bm b) + bm c = bm a + (bm b + bm c)`;
2. 交换律. `bm a + bm b = bm b + bm a`;
3. 加法零元. `bm a + bb 0 = bm a`;
4. 加法逆元. `bm a + (-bm a) = bb 0`.
总之, 向量空间关于向量的加法成一 Abel 群.

向量 `bm a, bm b` 的减法定义为 `bm a - bm b = bm a + (-bm b)`.

三角不等式 对任意向量 `bm a, bm b`, ` | |bm a| - |bm b| | le |bm a + bm b| le |bm a| + |bm b|`.

向量的数乘

实数 `lambda` 与向量 `bm a` 的数乘运算结果为一向量, 它的大小定义为 `|lambda bm a| = |lambda| |bm a|`, 当 `lambda gt 0` 时, 定义 `lambda bm a` 的方向与 `bm a` 相同, `lambda lt 0` 时则与 `bm a` 相反.

向量数乘的性质 设 `bm a, bm b` 是任意向量, `lambda, mu in RR`, 则
1. `lambda (bm a + bm b) = lambda bm a + lambda bm b`;
2. `(lambda + mu) bm a = lambda bm a + mu bm a`;
3. `(lambda mu) bm a = lambda (mu bm a)`;
4. `1 bm a = bm a`.
于是, 向量空间关于向量的加法与数乘成一线性空间.

对任意向量 `bm a`, `|0 bm a| = bb 0`; 对任意实数 `lambda`, `lambda bb 0 = bb 0`.

设向量 `bm a != bb 0`, 则向量 `(bm a)/|bm a|` 与 `bm a` 同向, 且长度为 1. 称这一计算过程为 `bm a` 的单位化.

线性相关与线性无关

设 `bm a_1, cdots, bm a_n` 是一组向量, `k_1, cdots, k_n` 是一组实数, 则 `k_1 bm a_1 + cdots + k_n bm a_n` 是一个向量, 称为向量组 `bm a_1, cdots, bm a_n` 的一个线性组合. 称向量组 `bm a_1, cdots, bm a_n` 线性相关, 如果存在不全为零的系数 `k_1, cdots, k_n`, 使得 `sum_(i=1)^n k_i bm a_i = bb 0`. 否则称该向量组线性无关.

用同一起点的有向线段表示向量组中的每个向量. 若这些有向线段在同一直线 (同一平面) 上, 则称这个向量组是共线的 (共面的). 向量共线也称为平行, 记为 `bm a //// bm b`.

`bb 0` 与任意向量共线; 共线的向量组必共面; 两个向量一定共面.

向量 `bm a, bm b` 共线当且仅当 `bm a, bm b` 线性相关.

向量 `bm a, bm b, bm c` 共面当且仅当 `bm a, bm b, bm c` 线性相关.

向量的线性运算可以用来解决点的共线或共面问题, 直线的共点问题以及线段的定比分割问题.

设点 `O` 是任意一点. 证明: 点 `M` 在线段 `AB` 上当且仅当存在非负实数 `lambda, mu` 满足 `vec(OM) = lambda vec(OA) + mu vec(OB)`, 且 `lambda + mu = 1`. 这时也称 `vec(OM)` 是 `vec(OA)` 与 `vec(OB)` 的凸组合.

设点 `O` 是任意一点. 证明: 点 `A, B, C` 共线当且仅当存在不全为零为实数 `lambda, mu, nu`, 使得 `lambda vec(OA) + mu vec(OB) + nu vec(OC) = bb 0`, 且 `lambda + mu + nu = 0`.

几何空间的线性结构

几何空间 `V` 是空间中所有点的集合. 取定一点 `O`, 则几何 空间中的任一点 `M` 对应于向量 `vec(OM)`. 事实上, 对平移后能够重合的向量不加区分, 则几何空间 `V` 中的点与向量空间 `E^3` 中的向量是一一对应的.

仿射坐标系与直角坐标系

称 `E^3` 中任意三个线性无关向量 `{bm d_1, bm d_2, bm d_3}` 为 `E^3` 的一个基. 对任意 `bm x in E^3`, 若 `bm x` 能表示为基的线性组合, 即 `EE x_i in RR`, `i = 1, 2, 3`, `bm x = sum_(i=1)^3 x_i bm d_i`. 则称三元有序实数组 `(x_1, x_2, x_3)` 为 `bm x` 在基 `{bm d_1, bm d_2, bm d_3}` 下的仿射坐标, 简称坐标. 在仿射坐标给定 (或隐含给定) 的情况下, 简记为 `bm x = (x_1, x_2, x_3)`.

仿射坐标的存在唯一性 取定 `E^3` 的一个基, 则 `E^3` 中的任意向量在这个基下的的仿射坐标存在唯一.

考虑到向量与点的一一对应关系, 我们有:

`V` 中的一个点 `O` 与一个基 `{bm d_1, bm d_2, bm d_3}` 合在一起称为 `V` 的一个仿射标架或仿射坐标系, 记为 `{O";" bm d_1, bm d_2, bm d_3}`. 其中 `O` 称为原点. 把过原点 `O`, 且分别以 `bm d_1, bm d_2, bm d_3` 为方向的有向直线称为 `x` 轴, `y` 轴, `z` 轴, 统称为坐标轴. 每两根坐标轴决定的平面称为坐标平面, 即 `xy`, `yz`, `zx` 平面. 坐标平面把空间分为八个部分, 称为八个卦限, 在每个卦限内, 点的坐标的符号不变. 将右手拇指以外的四指从 `x` 轴方向弯向 `y` 轴方向, 且转角小于 `pi` 时, 如果拇指所指的方向与 `z` 轴方向在 `xy` 平面同侧, 则称此坐标系为右手系, 否则称为左手系.

设 `X in V`, 定义点 `X` 的仿射坐标为它的定位向量 `vec(OX)` 在基 `{bm d_1, bm d_2, bm d_3}` 下的仿射坐标 `(x_1, x_2, x_3)`. 在仿射坐标给定 (或隐含给定) 的情况下, 简记为 `X(x_1, x_2, x_3)`.

如果 `bm e_1, bm e_2, bm e_3` 两两垂直, 且都是单位向量, 则称 `{O";" bm e_1, bm e_2, bm e_3}` 为一个正交标架或直角标架, 或直角坐标系. 显然 `bm e_1, bm e_2, bm e_3` 不共面, 因此直角标架是特殊的仿射标架.

平面上的仿射坐标系与直角坐标系也可以类似地建立起来.

向量线性运算的坐标表示

取定仿射标架 `{O";" bm d_1, bm d_2, bm d_3}`, 设 `bm a` 的坐标是 `(a_1, a_2, a_3)`, `bm b` 的坐标是 `(b_1, b_2, b_3)`, 则
1. `bm a +- bm b` 的坐标是 `(a_1 +- b_1, a_2 +- b_2, a_3 +- b_3)`;
2. 设 `lambda in RR`, `lambda bm a` 的坐标是 `(lambda a_1, lambda a_2, lambda a_3)`.

向量的坐标等于其终点坐标减去其起点坐标.

考虑向量 `vec(BA)`, 设 `A, B` 的坐标分别是 `(a_1, a_2, a_3)`, `(b_1, b_2, b_3)`, 它们也分别是 `vec(OA)`, `vec(OB)` 的坐标. 所以 `vec(BA) = vec(OA) - vec(OB)` 的坐标是 `(a_1 - b_1, a_2 - b_2, a_3 - b_3)`.

向量的内积

射影和分量

设 `bb 0 != bm d in E^3`, 取平面 `pi` 垂直于 `bm d`, 在 `pi` 内取一组基 `bm d_1, bm d_2`. 由, 任意 `bm a in E^3` 可以唯一地分解成 `bm a = x bm d_1 + y bm d_2 + z bm d`. 记 `bm a_1 = z bm d`, `bm a_2 = x bm d_1 + y bm d_2`, 易知 `bm a_1 //// bm d`, `bm a_2 _|_ bm d`. 称 `bm d` 所在直线为轴, `pi` 为射影平面.
• 称 `bm a_1` 是 `bm a` 沿方向 `bm d` 的内射影或 `bm a` 在轴上的正投影, 记为 `cc P_(bm d)(bm a)`; 实数 `z` 称为 `bm a` 沿方向 `bm d` 的分量, 记为 `Pi_(bm d)(bm a)`;
• 称 `bm a_2` 是 `bm a` 沿方向 `bm d` 的外射影或 `bm a` 在射影平面上的正投影.

设 `bb 0 != bm d in E^3`, 则 `bm a in E^3` 沿 `bm d` 的分量为 `Pi_(bm d)(bm a) = |bm a| cos (:bm a, bm d:)`, `(:bm a, bm d:)` 是向量 `bm a` 与 `bm d` 之间的夹角.

内射影是从空间到轴上的线性变换, 分量是从空间到 `RR` 的线性映射. 设 `bm a, bm b in E^3`, `lambda in RR`, 则 `cc P_(bm d)(bm a + bm b) = cc P_(bm d)(bm a) + cc P_(bm d)(bm b)`, `quad cc P_(bm d)(lambda bm a) = lambda cc P_(bm d)(bm a)`. `Pi_(bm d)(bm a + bm b) = Pi_(bm d)(bm a) + Pi_(bm d)(bm b)`, `quad Pi_(bm d)(lambda bm a) = lambda Pi_(bm d)(bm a)`.

向量内积的定义与性质

内积定义为一个映射 `(*): V xx V to RR`: `bm a * bm b = |bm a| |bm b| cos (:bm a, bm b:)`. `bm a` 和 `bm b` 中有一个为 `bb 0` 时, 规定 `bm a * bm b = 0`.

1. 若 `bm a != bb 0`, 则 `bm a * bm b = bm a * cc P_(bm a)(bm b) = |bm a| Pi_(bm a)(bm b)`;
2. `|bm a| = sqrt(bm a * bm a)`;
3. 若 `bm a, bm b != bb 0`, 则 `cos (:bm a, bm b:) = (bm a * bm b)/(|bm a| |bm b|)`;
4. `bm a _|_ bm b` 当且仅当 `bm a * bm b = 0` (零向量与任意向量都垂直).

的 1 揭示了内积与分量的联系; 由 2 和 3 可见, 内积与空间中的长度和角度有关.

内积是正定的对称双线性函数. 设 `bm a, bm b, bm c in E^3`, `lambda in RR`, 则它们满足
1. 正定性 `bm a * bm a ge 0`, 等号成立当且仅当 `bm a = bb 0`;
2. 对称性. `bm a * bm b = bm b * bm a`;
3. 线性性. `(bm a + bm b) * bm c = bm a * bm c + bm b * bm c`, `quad (lambda bm a) * bm b = lambda (bm a * bm b)`.

在一般的 Euclid 空间或内积空间中, 往往先以定义内积, 再由 `|bm a| = sqrt(bm a * bm a)` 定义范数. 见高等代数和泛函分析.

1. 平行四边形四边长度的平方和 = 对角线长度的平方和;
2. 设三角形三边长为 `a`, `b`, `c`, 边 `a` 上的中线长为 `m_a`, 则 `4m_a^2 = 2(b^2+c^2)-a^2`;
3. 任意四边形四边长的平方和 = 对角线长的平方和 `+4 xx` 对角线中点连线长的平方.

证明:
1. 设 `bm a`, `bm b` 是平行四边形的一对邻边, 则 `|bm a + bm b|^2 + |bm a - bm b|^2` `= (bm a + bm b) * (bm a + bm b) + (bm a - bm b) * (bm a - bm b)` `= 2|bm a|^2 + 2|bm b|^2`.
2. 倍长中线可证.
3. 设四边形 `ABCD` 的对角线 `AC` 的中点是 `M`, 对角线 `BD` 的中点是 `N`. 在三角形 `NAC`, `ABD` 和 `CBD` 中分别应用 2. 的结论: `4 MN^2 = 2(AN^2 + CN^2) - AC^2`,
   `4 AN^2 = 2(AB^2 + AD^2) - BD^2`,
   `4 CN^2 = 2(CB^2 + CD^2) - BD^2`. 将后两式相加代入第一式, 消去 `AN^2 + CN^2`, 得 `AB^2 + BC^2 + CD^2 + DA^2 = AC^2 + BD^2 + 4MN^2`

向量内积的坐标表示

仿射标架

取定仿射标架 `{O";" bm d_1, bm d_2, bm d_3}`, `bm a = (a_1, a_2, a_3)`, `bm b = (b_1, b_2, b_3)`, 则 ` bm a * bm b = (sum_(i=1)^3 a_i bm d_i) * (sum_(j=1)^3 b_j bm d_j) = sum_(i=1)^3 sum_(j=1)^3 a_i b_j bm d_i * bm d_j`. 因此只要知道 `bm d_1, bm d_2, bm d_3` 之间的内积 (9 个数, 由对称性, 实质上只有 6 个数), 就可以求出任意两个向量的内积. 这 9 个数称为仿射标架 `{O";" bm d_1, bm d_2, bm d_3}` 的度量参数.

正交标架

特别当所取的仿射标架为正交标架 `{O";" bm e_1, bm e_2, bm e_3}` 时, `bm e_i * bm e_j = delta_(ij)`, `i, j = 1, 2, 3`. 其中 `delta_(ij) = { 1, if i = j; 0, if i != j :}` 称为Kroneker 符号. 因此在正交标架下, `bm a * bm b = sum_(i=1)^3 a_i b_i`. 联系, 在正交标架下, 向量 `bm a = (a_1, a_2, a_3)` 的长度为 `|bm a| = sqrt(sum_(i=1)^3 a_i^2)`, 空间中两点 `X(x_1, x_2, x_3)`, `Y(y_1, y_2, y_3)` 的距离为 `|vec(XY)| = sqrt(sum_(i=1)^3 (x_i - y_i)^2)`.

方向角, 方向余弦

取正交标架 `{O";" bm e_1, bm e_2, bm e_3}`, 任取向量 `bm a = sum_(j=1)^3 a_j bm e_j`, 两边与 `bm e_i` 作内积得 ` bm a * bm e_i = sum_(j=1)^3 a_j bm e_i * bm e_j = sum_(j=1)^3 a_j delta_(ij) = a_i`, `i = 1, 2, 3`. 说明在正交标架下, `bm a` 与基向量 `bm e_i` 的内积就是 `bm a` 的第 `i` 个坐标. 特别, 当 `bm a` 为单位向量时, 又有 ` a_i = bm a * bm e_i = cos (:bm a, bm e_i:)`. 角 `(:bm a, bm e_i:)`, `i = 1, 2, 3`, 称为方向 `bm a` 方向角, 其余弦值称为方向 `bm a` 的方向余弦. 由 `|bm a| = 1` 知 `sum_(i=1)^3 cos^2 (:bm a, bm e_i:) = 1`. 所以方向余弦的平方和恒等于 1.

向量的外积

向量外积的定义与性质

外积定义为映射 `(xx): V xx V to V`: `|bm a xx bm b| = |bm a| |bm b| sin (:bm a, bm b:)`, 当 `|bm a xx bm b| != 0` 时, 它的方向服从右手定则, 即当右手四指从 `bm a` 以小于 `pi` 的转角弯向 `bm b` 时, 拇指就指向 `bm a xx bm b`: `bm a xx bm b _|_ bm a`, `quad` `bm a xx bm b _|_ bm b`, `quad` `(bm a, bm b, bm a xx bm b)` 成右手系. `bm a` 和 `bm b` 中有一个为 `bb 0` 时, 规定 `bm a xx bm b = bb 0`.

1. `bm a //// bm b` 当且仅当 `bm a xx bm b = 0` (零向量与任意向量都共线).
2. 设 `bm a != bb 0`, 则对任意 `bm b in E^3`, 令 `bm b_2` 是 `bm b` 沿方向 `bm a` 的外射影, 则 `bm a xx bm b = bm a xx bm b_2`,

外积是反对称双线性映射. 设 `bm a, bm b, bm c in E^3`, `lambda in RR`, 则它们满足:
1. 反交换律. `bm b xx bm a = -(bm a xx bm b)`;
2. 线性性. `(bm a + bm b) xx bm c = bm a xx bm c + bm b xx bm c`, `quad (lambda bm a) xx bm b = lambda (bm a xx bm b)`.

一般的空间中, 可以将满足的映射定义为外积. 如微分几何中的外微分就满足上述外积的性质.

向量外积的坐标表示

仿射标架

取定仿射标架 `{O";" bm d_1, bm d_2, bm d_3}`, `bm a = (a_1, a_2, a_3)`, `bm b = (b_1, b_2, b_3)`, 则 ` bm a xx bm b = (sum_(i=1)^3 a_i bm d_i) xx (sum_(j=1)^3 b_j bm d_j)` `= (a_2 b_3 - a_3 b_2) bm d_2 xx bm d_3 + (a_3 b_1 - a_1 b_3) bm d_3 xx bm d_1 + (a_1 b_2 - a_2 b_1) bm d_1 xx bm d_2` `= |bm d_2 xx bm d_3, bm d_3 xx bm d_1, bm d_1 xx bm d_2; a_1, a_2, a_3; b_1, b_2, b_3|`. 因此只要知道 `bm d_1, bm d_2, bm d_3` 之间的外积, 就可以求出任意两个向量的外积.

右手正交标架

设 `bm e` 是单位向量, `bm b _|_ bm e`, 则 `bm e xx bm b` 等于 `bm b` 在以 `bm e` 为法向量的平面上按右手法则旋转一个直角得到的向量.

现在取右手正交标架 `{O";" bm e_1, bm e_2, bm e_3}`, 由 有 `bm e_1 xx bm e_2 = bm e_3`, `quad` `bm e_2 xx bm e_3 = bm e_1`, `quad` `bm e_3 xx bm e_1 = bm e_2`. 于是 ` bm a xx bm b = |bm e_1, bm e_2, bm e_3; a_1, a_2, a_3; b_1, b_2, b_3|`, ` |bm a xx bm b| = sqrt( |a_2, a_3; b_2,b_3|^2 + |a_3, a_1; b_3,b_1|^2 + |a_1, a_2; b_1,b_2|^2 )`.

向量的混合积

平面向量混合积的定义与性质

曲面的一个法向量称为它的一个定向. 规定当右手拇指指向所给定的法向量时, 右手四指的环绕方向就是曲面上的绕行方向. 这个绕行方向也称为曲面的定向.

设 `bm n` 是平面 `pi` 的一个单位法向量, `bm a, bm b in pi`. 由外积定义, `bm n //// bm a xx bm b`, 由于 `bm n != bb 0`, 存在唯一的 `lambda in RR` 使得 `bm a xx bm b = lambda bm n`. 称 `lambda` 为 `bm a` 与 `bm b` 关于定向 `bm n` 的平面向量混合积, 记为 `(bm a, bm b)`. 由定义, `bm a xx bm b = (bm a, bm b) bm n`. `bm a, bm b` 不共线时, 以 `bm a, bm b` 为邻边的平行四边形的定向面积或有向面积是指, 当 `bm a, bm b, bm n` 成右手系时, 定向面积等于面积; 否则定向面积等于面积的相反数. 这个定向面积恰好等于 `(bm a xx bm b)`.

1. 两向量共线当且仅当 `(bm a, bm b) = 0`;
2. `(bm a, bm b) = -(bm b, bm a)`.

平面向量混合积的坐标表示

在平面上取定仿射标架 `{O";" bm d_1, bm d_2}`, 令 `bm d_3 = bm d_1 xx bm d_2` 为平面的定向, 则 `{O";" bm d_1, bm d_2, bm d_3}` 是空间中的仿射标架, 且为右手系. 设 `bm a = a_1 bm d_1 + a_2 bm d_2`, `bm b = b_1 bm d_1 + b_2 bm d_2`, 因为 ` bm a xx bm b = |bm d_2 xx bm d_3, bm d_3 xx bm d_1, bm d_1 xx bm d_2; a_1, a_2, 0; b_1, b_2, 0|` `= |a_1, a_2; b_1, b_2| bm d_3`, 所以 ` (bm a, bm b) = |a_1, a_2; b_1, b_2| |bm d_3|`.

特别取右手正交标架 `{O";" bm e_1, bm e_2}` 时, `(bm a, bm b) = |a_1, a_2; b_1, b_2|`.

两向量共线的条件 (仿射坐标)

平面上两向量 `bm a = (a_1, a_2)`, `bm b = (b_1, b_2)` 共线当且仅当它们所围的平行四边形的定向面积 `|a_1, a_2; b_1, b_2| = 0`.

平面上三点 `A(a_1, a_2)`, `B(b_1, b_2)`, `C(c_1, c_2)` 共线当且仅当它们所围的三角形的定向面积 `1/2 |a_1, a_2, 1; b_1, b_2, 1; c_1, c_2, 1| = 0`.

二重外积公式

二重外积公式 设 `bm a, bm b, bm c in E^3`, 则 ` bm a xx (bm b xx bm c) = (bm a * bm c) bm b - (bm a * bm b) bm c` `= |bm b, bm c; bm a * bm b, bm a*bm c|`.

Jacobi 等式 `sum bm a xx (bm b xx bm c) = bb 0`. 上式遵循轮换求和约定, 相当于 `bm a xx (bm b xx bm c) + bm b xx (bm c xx bm a) + bm c xx (bm a xx bm b) = bb 0`.

向量混合积的定义与性质

混合积定义为映射 `(*,*,*): V^3 to RR`: `(bm a, bm b, bm c) = bm a xx bm b * bm c`. 为使上式有意义, 应当先作外积, 再作内积.

给定空间中不共面的三向量 `bm a, bm b, bm c`, 由它们确定的平行六面体的定向体积或有向体积是指, 当 `bm a, bm b, bm c` 成右手系时, 定向体积等于体积; 否则定向体积等于体积的相反数. 由向量混合积的定义, 这定向体积恰好等于 `(bm a, bm b, bm c)`.

三向量 `bm a, bm b, bm c` 共面当且仅当 `(bm a, bm b, bm c) = 0`.

`bm a, bm b, bm c` 共面 `iff bm a xx bm c` 与 `bm a xx bm b` 共线 `iff (bm a xx bm b) xx (bm a xx bm c) = bb 0` `iff (bm a xx bm b * bm c) bm a - (bm a xx bm b * bm a) bm c = bb 0` `iff bm a xx bm b * bm c = 0`.

混合积具有轮换对称性. `(bm a, bm b, bm c) = (bm b, bm c, bm a) = (bm c, bm a, bm b)`. 由上式得 `bm a xx bm b * bm c = bm b xx bm c * bm a = bm a * bm b xx bm c`. 因此, 将混合积定义为 `bm a * bm b xx bm c` 也是一样的. 进一步可证, 交换混合积中任意两项, 结果相差一个负号.

混合积的坐标表示

取定仿射标架 `{O";" bm d_1, bm d_2, bm d_3}`, `bm a = (a_1, a_2, a_3)`, `bm b = (b_1, b_2, b_3)`, `bm c = (c_1, c_2, c_3)`, 则 ` (bm a, bm b, bm c) = bm a * bm b xx bm c` `= |bm d_2 xx bm d_3, bm d_3 xx bm d_1, bm d_1 xx bm d_2; b_1, b_2, b_3; c_1, c_2, c_3| * sum_(i=1)^3 a_i bm d_i` `= |a_1, a_2, a_3; b_1, b_2, b_3; c_1, c_2, c_3| (bm d_1, bm d_2, bm d_3)`.

特别, 当取定的标架为右手正交标架 `{O";" bm e_1, bm e_2, bm e_3}` 时, `(bm e_1, bm e_2, bm e_3) = 1`. 所以 `(bm a, bm b, bm c)` `= |a_1, a_2, a_3; b_1, b_2, b_3; c_1, c_2, c_3|`.

三向量共面的条件 (仿射坐标)

空间中三向量 `bm a = (a_1, a_2, a_3)`, `bm b = (b_1, b_2, b_3)`, `bm c = (c_1, c_2, c_3)` 共面当且仅当它们所围的平行六面体的定向体积 `|a_1, a_2, a_3; b_1, b_2, b_3; c_1, c_2, c_3| = 0`.

空间中四点 `A(a_1, a_2, a_3)`, `B(b_1, b_2, b_3)`, `C(c_1, c_2, c_3)`, `D(d_1, d_2, d_3)` 共面当且仅当它们所围的四面体的定向体积 `1/6 |a_1, a_2, a_3, 1; b_1, b_2, b_3, 1; c_1, c_2, c_3, 1; d_1, d_2, d_3, 1| = 0`.

Lagrange 恒等式

Lagrange 恒等式 设 `bm a_1, bm a_2, bm b_1, bm b_2 in E^3`, 则 ` (bm a_1 xx bm a_2) * (bm b_1 xx bm b_2) = |bm a_1 * bm b_1, bm a_1 * bm b_2; bm a_2 * bm b_1, bm a_2 * bm b_2| = "det"(bm a_i * bm b_j)_(2 xx 2)`.

利用混合积的轮换对称性与二重外积公式, 左边 = `bm a_2 xx (bm b_1 xx bm b_2) * bm a_1 = |bm b_1, bm b_2; bm a_2 * bm b_1, bm a_2 * bm b_2| * bm a_1` = 右边.

1. `|bm a xx bm b|^2 + (bm a * bm b)^2 = |bm a|^2 |bm b|^2`;
2. `(bm a_1, bm a_2, bm a_3)(bm b_1, bm b_2, bm b_3) = "det"(bm a_i * bm b_j)_(3 xx 3)`;
3. `(bm a, bm b, bm c)^2 = (bm a xx bm b, bm b xx bm c, bm c xx bm a)`;
4. `sum_(bm a, bm b, bm c) (bm a xx bm b) * (bm c xx bm d) = 0`;
5. `bm a_1 xx (bm a_2 xx (bm b_1 xx bm b_2)) = | bm a_1 xx bm b_1, bm a_1 xx bm b_2; bm a_2 * bm b_1, bm a_2 * bm b_2|`;
6. ` (bm a xx bm b) xx (bm c xx bm d) = (bm c, bm d, bm a) bm b - (bm b, bm c, bm d) bm a` `= (bm d, bm a, bm b) bm c - (bm a, bm b, bm c) bm d`.

1. 用 Lagrange 恒等式计算 `|bm a xx bm b|^2`;
2. 用坐标计算, 注意矩阵乘积的行列式等于行列式的乘积;

(二维勾股定理) 直角三棱锥的斜面面积的平方等于其他三个直角面面积的平方和.

设 `OABC` 是直角三棱锥, `O` 为直角顶点, 于是 `angle AOB, angle BOC, angle COA` 是直角, `triangle ABC` 是它的斜面. 分别记 `vec(OA), vec(OB), vec(OC)` 为 `bm a, bm b, bm c`, 则 `bm a * bm b = bm b * bm c = bm c * bm a = 0`. 由的 1 有 `{: |vec(AB) xx vec(AC)|^2 ,= |vec(AB)|^2 |vec(AC)|^2 - (vec(AB)*vec(AC))^2; ,= (|bm a|^2 + |bm b|^2) (|bm a|^2 + |bm c|^2) - ((bm b - bm a) * (bm c - bm a))^2; ,= (|bm a|^2 + |bm b|^2) (|bm a|^2 + |bm c|^2) - |bm a|^4; ,= |bm a|^2 |bm b|^2 + |bm b|^2 |bm c|^2 + |bm c|^2 |bm a|^2. :}` 即得证.

四元数与三维旋转*

Hamilton 四元数形如 `q = w + x i + y j + z k`, 其中 `w, x, y, z in RR`, `i^2 = j^2 = k^2 = i j k = -1`. 四元数之间的乘法由上式及分配律完全定义, 该乘法不满足交换律, 且每个非零的四元数都有乘法逆元, 即, 四元数关于该乘法构成一个除环.

`k^2 = -1` 两边同时右乘 `k^-1` 得 `k = -k^-1`, 即 `k^-1 = -k`. 同理 `i^-1 = -i`, `quad j^-1 = -j`, `quad k^-1 = -k`. 我们来说明 `i, j, k` 之间的乘法不可交换: `i j k = -1` 两边同时右乘 `k` 得 `-i j = - k`, 即 `i j = k`; 继续两边同时右乘 `j` 得 `-i = k j`. 类似也可以施以左乘, 最终得到 `i j = k = - j i`, `quad j k = i = - k j`, `quad k i = j = - i k`.

四元数的三角形式 一个四元数可以看作标量部分 `w` 与矢量部分 `bm v = x i + y j + z k` 之和. `bm v` 是基底 `i, j, k` 张成的三维线性空间中的向量. 四元数的长度 (模) 定义为 `|q| = sqrt(w^2+x^2+y^2+z^2)` `= sqrt(w^2 + v^2) quad`, 其中 `v = |bm v|`. 于是, 四元数可以写为模长与单位 (长度的) 四元数的乘积 `q = |q| hat q`, 单位四元数有三角表示 `hat q = cos theta + hat bm v sin theta`, `quad hat bm v` 为单位向量. 因为实数与四元数的乘法可交换, 两个四元数相乘, 可以把它们的模长与单位四元数分别相乘: `q_1 q_2 = |q_1| |q_2| hat q_1 hat q_2`.

在四元数乘法的意义下,
1. `bm v_1 bm v_2 = bm v_1 xx bm v_2 - bm v_1 * bm v_2`;
2. `(w_1 + bm v_1)(w_2 + bm v_2)` `= (w_1 w_2 - bm v_1 * bm v_2) + w_1 bm v_2 + w_2 bm v_1 + bm v_1 xx bm v_2`;
3. (类比 De Moivre 公式) `(cos alpha + bm e sin alpha)(cos beta + bm e sin beta)` `= cos (alpha+beta) + bm e sin(alpha+beta)`, `bm e` 为任意单位向量;
4. `(cos alpha + bm e sin alpha)^-1 = cos alpha - bm e sin alpha`, `bm e` 为任意单位向量.

2, 3, 4. 是 1. 的直接推论. 下证 1. 设 `bm v_lambda = x_lambda i + y_lambda j + z_lambda k`, `lambda = 1, 2`, 则左边等于 `(x_1, y_1, z_1) [i;j;k] (i, j, k) [x_2;y_2;z_2]` `= (x_1, y_1, z_1) [-1, k, -j; -k, -1, i; j, -i, -1] [x_2;y_2;z_2]` `= -(x_1 x_2 + y_1 y_2 + z_1 z_2) + (y_1 z_2 - z_2 y_1) i` `+ (z_1 x_2 - x_2 z_1) j + (x_1 y_2 - x_2 y_1) k`, 等于右边.

三维旋转公式 三维向量 `bm v` 绕单位向量 `bm e` 按右手螺旋方向旋转 `theta` 角, 所得结果向量 `bm v'` 有
1. 向量表示 (Rodrigues 旋转公式) `bm v' = bm v^|| + bm v^_|_ cos theta + bm e xx bm v sin theta`, 其中 `bm v^||`, `bm v^_|_` 分别是 `bm v` 的平行和垂直 `bm e` 的分量.
2. 矩阵表示 `bm v' = bm T bm v`, 其中 `bm e = (a, b, c)^T`, `bm T = (1-cos theta) bm e bm e^T` `+ cos theta bm I` `+ sin theta [ 0, -c, b; c, 0, -a; -b, a, 0 ]`.
3. 四元数表示 `bm v' = q bm v q^-1`, `quad q = cos(theta//2) + bm e sin(theta//2)`.

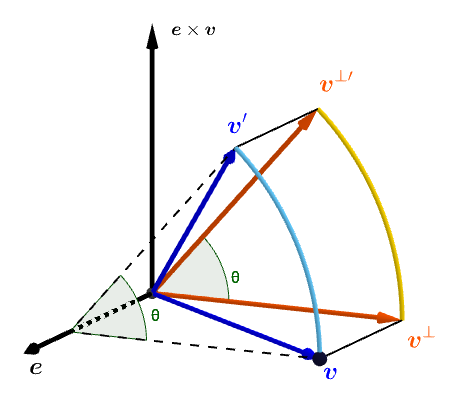
1. 设 `bm e` 与 `bm v` 不共线, 由二重外积公式, 将 `bm v` 分解到平行 `bm e` 和垂直 `bm e` 的方向上: `bm v = bm v^|| + bm v^(_|_)` `= (bm v * bm e) bm e + (bm e xx bm v) xx bm e`. 如图, `bm e, bm v^(_|_), bm e xx bm v` 成右手系. `bm v'` 等于将 `bm v^(_|_)` 旋转 `theta` 角后, 再加上 `bm v^||`: `bm v' = bm v^|| + bm v^(_|_) cos theta + bm e xx bm v sin theta`.
2. 记 `bm v = (x, y, z)`, `k = bm v * bm e` `= a x + b y + c z`, 于是 `bm v^|| = (k a, k b, k c)`, `quad bm v^_|_ = bm v - bm v^||` `= (x - k a, y - k b, z - k c)`. 由 1. 得 `bm v' = [ k a + (x-k a) cos theta + (b z-c y) sin theta; k b + (y-k b) cos theta - (a z-c x) sin theta; k c + (z-k c) cos theta + (a y-b x) sin theta; ]`, 考虑各分量中 `x, y, z` 的系数, 就得到矩阵 `bm T`.
3. 记 `alpha = theta//2`, 有 `q bm v q^-1` `= (cos alpha + bm e sin alpha) bm v (cos alpha - bm e sin alpha)`
   `= bm v cos^2 alpha - bm (e v e) sin^2 alpha` `+ (bm e bm v - bm v bm e) sin alpha cos alpha`
   `= bm v cos^2 alpha - bm (e v e) sin^2 alpha` `+ 2 bm e xx bm v sin alpha cos alpha`. `bm (e v e)` 可以分解为以下两式之和: `bm (e v)^|| bm e` `= -(bm v * bm e) bm e` `= - bm v^||`,
   `bm (e v^(_|_) e)` `= (bm e xx bm v^(_|_)) xx bm e` `= bm v^(_|_)`, 从而 `q bm v q^-1` `= (bm v^|| + bm v^(_|_))cos^2 alpha + (bm v^|| - bm v^(_|_))sin^2 alpha` `+ bm e xx bm v sin theta` `= bm v'`.

Euler 角的旋转合成 [来自 Unity Shader 入门精要] 给定一个旋转顺序 (例如zxy), 以及它们对应的旋转角度 `(θ_x, θ_y, θ_z)`, 有两种方式可以选择:
1. 绕坐标系 `E` 下的 `z` 轴旋转 `θ_z`, 绕坐标系 `E` 下的 `y` 轴旋转 `θ_y`, 绕坐标系 `E` 下的 `x` 轴旋转 `θ_x`, 即旋转时坐标系不动.
2. 绕坐标系 `E` 下的 `z` 轴旋转 `θ_z`, 绕新坐标系 `E'` 下的 `y` 轴旋转 `θ_y`, 绕最新坐标系 `E''` 下的 `x` 轴旋转 `θ_x`, 即在旋转时, 把坐标系一起转动.
有趣的是, 按第一种方式进行旋转, 和按相反次序进行第二种旋转效果是相同的. 即 `旋转_1(z x y) = 旋转_2(y x z)`. 例如, 绕 x 轴、y 轴旋转 90 度的变换分别为 `R_x = [1, 0, 0; 0, cos 90^@, -sin 90^@; 0, sin 90^@, cos 90^@]`, `quad R_y = [cos 90^@, 0, sin 90^@; 0, 1, 0; -sin 90^@, 0, cos 90^@]`. 空间中一点 `r = [0, 0, 1]^(sf T)` 经过变换 `R_x R_y r` 的结果是 `[1, 0, 0]^(sf T)`. 可以验证, 这相当于先绕 x 轴旋转 90 度, 然后绕新 y 轴旋转 90 度; 同时, 也相当于先绕 y 转旋转 90 度, 然后绕原 x 轴旋转 90 度.