本章结合坐标法与向量法, 利用仿射坐标系研究空间中的平面与直线.

平面的线性性质

平面的参数方程和普通方程

向量 `bm v` 与平面 `pi` 平行与 `bm v` 在 `pi` 上等同, 记为 `bm v //// pi`.

取定仿射标架 `{O";" bm d_1, bm d_2, bm d_3}`, 设 `P_0(x_0, y_0, z_0)`, 向量 `bm r_1 = (x_1, y_1, z_1)` 和 `bm r_2 = (x_2, y_2, z_2)` 线性无关, 则点 `P_0` 和向量 `bm r_1, bm r_2` 唯一确定了平面 `pi`, 使得 `P_0 in pi`, `bm r_i //// pi`, `i = 1, 2`. 我们有 点 `P` 落在由 `P_0`, `bm r_1, bm r_2` 确定的平面上当且仅当 `vec(P_0 P), bm r_1, bm r_2` 线性相关. 由于 `bm r_1, bm r_2` 线性无关, 所以 `vec(P_0 P)` 可以唯一表示为 `vec(P_0 P) = u bm r_1 + v bm r_2`, `u, v in RR`. 改写得到平面的参数方程 `{ x = x_0 + x_1 u + x_2 v; y = y_0 + y_1 u + y_2 v; z = z_0 + z_1 u + z_2 v; :}` `quad` `u, v in RR`.

另一方面, 平面 `pi` 的方程也可以是 `(vec(P_0 P), bm r_1, bm r_2) = 0`, 即 `|x-x_0, y-y_0, z-z_0; x_1, y_1, z_1; x_2, y_2, z_2| = 0`. 令 `A = |y_1, z_1; y_2, z_2|`, `B = |z_1, x_1; z_2, x_2|`, `C = |x_1, y_1; x_2, y_2|`, `D = -(Ax_0 + By_0 + Cz_0)`, 上式化为平面的普通方程 `Ax + By + Cz + D = 0`. 由于 `bm r_1, bm r_2` 线性无关, `bm r_1 xx bm r_2 != bb 0`, 所以 `A, B, C` 不全为零, 平面的普通方程是三元一次方程.

仿射坐标系下, 平面的方程是三元一次方程, 反之可以验证, 由 `P_0(-D//A, 0, 0)`, `bm r_1 = (-B//A, 1, 0)`, `bm r_2 = (-C//A, 0, 1)` 确定的平面方程正好是 `Ax + By + Cz + D = 0`, 所以任意三元一次方程表示一个平面.

向量 `bm w = (x_0, y_0, z_0)` 与平面 `Ax + By + Cz + D = 0` 平行当且仅当它适合齐次方程 `Ax_0 + By_0 + Cz_0 = 0`.

`x` 轴 (`y` 轴, `z` 轴) 与平面 `pi: Ax + By + Cz + D = 0` 平行或落在平面上当且仅当 `A = 0` (`B = 0`, `C = 0`); 原点落在平面 `pi` 上当且仅当 `D = 0`.

平面的相对位置

设平面 `pi_1`, `pi_2` 的方程分别为 `A_i x + B_i y + C_i z + D_i = 0`, `i = 1, 2`. 则
1. `pi_1` 与 `pi_2` 相交当且仅当两方程的一次项系数不成比例;
2. `pi_1` 与 `pi_2` 平行当且仅当两方程的一次项系数成比例, 但与常数项不成比例;
3. `pi_1` 与 `pi_2` 重合当且仅当两方程的所有系数成比例.

由 Cramer 法则知道, 三平面 `A_i x + B_i y + C_i z + D_i = 0`, `i = 1, 2, 3` 恰有一个公共点当且仅当 `|A_1, B_1, C_1; A_2, B_2, C_2; A_3, B_3, C_3| != 0`.

平面方程小集

约定 `P = (x, y, z)`, `varphi(P) = Ax + By + Cz`, `f(P) = varphi(P) + D`.

2. 首先容易验证 `(a,0,0)`, `(0,b,0)`, `(0,0,c)` 三点适合方程; 其次所给方程是三元一次方程, 它表示一个平面. 由几何知识知道, 过不共线三点的平面是唯一的.
3. 由四点共面的充要条件立即得到.
5. 依题意, 点 `P` 落在 `pi` 上当且仅当 `vec(P_0 P) _|_ bm n`. 所以 `pi` 的方程是 `vec(P_0 P) * bm n = 0`, 即 `A(x - x_0) + B(y - y_0) + C(z - z_0) = 0`.

1. 几何空间中经过同一直线的所有平面组成的集合称为有轴平面束, 这条直线称为平面束的轴. 容易看出, 由两相交平面 `pi_1`, `pi_2` 确定的有轴平面束由 `pi_1`, `pi_2` 的全体线性组合构成.
2. 由 "一点一平面" 的结果知道, 满足 `Ax + By + Cz = delta` 的点的轨迹是一平面, 与平面 `pi: Ax + By + Cz + D = 0` 平行 (或重合). 当参数 `delta` 变化时, 上述方程取遍全体与平面 `pi` 平行的平面族.
3. 由点法式知道, 正交标架下, `(A, B, C)` 是平面 `Ax + By + Cz + D = 0` 的一个法向量. 另外, 两平面垂直当且仅当它们的法向量垂直, 即 `bm n_1 * bm n_2 = 0`, 亦即 `A_1 A_2 + B_1 B_2 + C_1 C_2 = 0`.

三元一次不等式的几何意义

设点 `P_0` 在平面 `f(P) = 0` 上, `P_0, P_1, P_2` 三点共线, 则 `f(P_1) vec(P_0 P_2) = f(P_2) vec(P_0 P_1)`.

方程 `f(P) = 0` 可以写成 `varphi(P) + D = 0`, 其中 `varphi` 是线性函数. 由 `P_0` 在平面上得 `varphi(P_0) = -D`.
若 `P_1` 不在平面上, 有 `varphi(P_1) != varphi(P_0)`, 即 `varphi(P_1 - P_0) != 0`. 由 `P_0, P_1, P_2` 三点共线, 且 `vec(P_0 P_1) != bb 0` 知, 存在 `k in RR` 使 `vec(P_0 P_2) = k vec(P_0 P_1)`, 于是 `varphi(P_2 - P_0) = k varphi(P_1 - P_0)`. 从而 ` k = (varphi(P_2 - P_0)) / (varphi(P_1 - P_0)) = (varphi(P_2) - varphi(P_0)) / (varphi(P_1) - varphi(P_0))` `= (varphi(P_2) + D) / (varphi(P_1) + D) = f(P_2) / f(P_1)`. 现在设 `P_1` 在平面上, 即 `f(P_1) = 0`. 若 `P_1 = P_0`, 结论已经成立; 若 `P_1 != P_0`, 则 `P_1, P_0` 是平面上不同的两点, 连接它们的直线必定位于该平面上, 故 `f(P_2) = 0`, 结论也成立.

设平面 `pi: f(P) = 0`, 则空间中全体适合不等式 `f(P) gt 0` 的点位于平面 `pi` 的同侧; 全体适合不等式 `f(P) lt 0` 的点位于平面 `pi` 的另一侧.

将方程 `f(P) = 0` 写为 `varphi(P) + D = 0`, 其中 `varphi` 是线性函数. 在空间中取两点 `P_1, P_2`.
1. 若 `f(P_1) = f(P_2)`, 即 `varphi(P_1 - P_2) = 0`. 由, `vec(P_1 P_2)` 平行于平面, 于是 `P_1, P_2` 位于平面同侧.
2. 若 `f(P_1) f(P_2) gt 0`, 且 `f(P_1) != f(P_2)`, `vec(P_1 P_2)` 与平面不平行. 设直线 `P_1 P_2` 与平面交于点 `P_0`. 由, `vec(P_0 P_1)` 与 `vec(P_0 P_2)` 同向, 即 `P_1, P_2` 位于平面同侧.
3. `f(P_1) f(P_2) lt 0` 时可类似证明, `P_1, P_2` 位于平面异侧.

平面的度量性质

点到平面的距离

设 `bm n` 是平面的一个单位法向量, `P_0` 是平面上一点, 空间一点 `P` 在平面上的射影 (即垂足) 是 `P_1`, 则 `vec(P_1 P) = (vec(P_0 P) * bm n) bm n`, 于是 `P` 到该平面的距离为 `|vec(P_1 P)| = |vec(P_0 P) * bm n|`.

由 `vec(P_1 P) //// bm n` 知, 存在唯一的 `delta in RR`, 使 `vec(P_1 P) = delta bm n`. 上式两边与 `bm n` 作内积, ` delta = delta bm n * bm n = vec(P_1 P) * bm n = cc P_(bm n)(vec(P_0 P)) * bm n = vec(P_0 P) * bm n`.

正交标架下点到平面的垂向量, 点到平面的距离及对称点 正交标架下, 设空间一点 `P(x, y, z)` 在平面 `Ax + By + Cz + D = 0` 上的射影是 `P_1`, 则 `vec(P_1 P) = (A x+B y+C z+D) bm n/|bm n|^2`, 其中 `bm n = (A, B, C)` 是平面的法向量. 于是 `P` 到该平面的距离为 ` |vec(P_1 P)| = |A x+ B y+C z+D|/sqrt(A^2+B^2+C^2)`. 又设 `Q` 是 `P` 关于该平面的对称点, 则 `vec(PQ) = -2 vec(P_1 P)`.

选取平面上一点 `P_0(x_0, y_0, z_0)`, 则 `-(A x_0+B y_0+C z_0) = D`. 由, ` vec(P_1 P) = (vec(P_0 P) * (bm n)/|bm n|) (bm n)/|bm n|` `= (A(x-x_0) + B(y-y_0) + C(z-z_0)) (bm n)/|bm n|^2` `= (A x+B y+C z+D) (bm n)/|bm n|^2`.

称满足 `vec(P_1 P) = delta (bm n)/|bm n|` 的实数 `delta = (Ax_P + By_P + Cz_P + D)/sqrt(A^2+B^2+C^2)` 为点 `P` 到平面 `Ax + By + Cz + D = 0` 的离差. 离差的绝对值等于点到平面的距离, 符号与单位法向量的选取有关.

正交标架下, 两平行平面 `pi_1: Ax + By + Cz + D_1 = 0`,
`pi_2: Ax + By + Cz + D_2 = 0` 的距离 `d = |D_1 - D_2|/sqrt(A^2 + B^2 + C^2)`.

选取点 `(x_2, y_2, z_2) in pi_2`, 则 `Ax_2 + By_2 + Cz_2 = -D_2`. 由, ` d = |Ax_2 + By_2 + Cz_2 + D_1|/sqrt(A^2+B^2+C^2) = |D_1 - D_2|/sqrt(A^2+B^2+C^2)`.

两平面的夹角

两平面的夹角是指两平面交成四个二面角中的任一个, 也指两平面的法向量之间的夹角或其补角. 由定义知道, 两平行 (或重合) 平面的夹角等于 `0` 或 `pi`.

正交标架下, 两平面 `pi_1: A_1 x + B_1 y + C_1 z + D = 0`,
`pi_2: A_2 x + B_2 y + C_2 z + D = 0` 的一个夹角 `theta` 满足 `cos theta = (bm n_1 * bm n_2)/(|bm n_1| |bm n_2|) = (A_1 A_2 + B_1 B_2 + C_1 C_2) / (sqrt(A_1^2 + B_1^2 + C_1^2) sqrt(A_2^2 + B_2^2 + C_2^2))`. `cos theta gt 0` 时 `theta` 为锐角, `cos theta lt 0` 时 `theta` 为钝角, `cos theta = 0` 时 `theta` 为直角.

平面上直线的若干性质与事实

因为平面上直线的性质与事实可以完全类似于空间中的平面建立起来, 我们不拟作重复的推导, 只将若干平行的事实罗列如下:
• 在平面仿射标架 `{O";" bm d_1, bm d_2}` 下, 由点 `P_0(x_0,y_0)` 和向量 `bm r_1 = (x_1,y_1) != bb 0` 唯一确定了直线 `l`, 使得 `P_0 in l`, `bm r_1 //// l`. 且点 `P` 落在直线 `l` 上当且仅当 `vec(P_0 P) //// r_1`: `vec(P_0 P) = t bm r_1`, `quad t in RR`. 直线的参数方程是 `{ x = x_0 + x_1 t; y = y_0 + y_1 t; :}` `quad t in RR`.
  另一方面由 `(vec(P_0 P), bm r_1)` `= | x-x_0,y-y_0; x_1, y_1 |` `= 0`, 得到普通方程 `A x + B y + C = 0`.
• 平面仿射标架下, 直线的方程是二元一次方程, 反之任意二元一次方程表示一条直线.
• 向量 `bm w = (x_0,y_0)` 与直线 `A x + B y + C = 0` 平行当且仅当它适合齐次方程 `A x_0 + B y_0 = 0`.
• `x` 轴 (`y` 轴) 与直线 `l: A x + B y + C = 0` 平行或重合当且仅当 `A = 0` (`B = 0`); `l` 过原点当且仅当 `C = 0`.
• 两直线 `A_i x + B_i y + C_i = 0`, `i = 1, 2` 相交当且仅当两方程的一次项系数不成比例, 此时两直线恰有一个公共点: 由 Cramer 法则, 这当且仅当 `|A_1,B_1; A_2,B_2| != 0`; 两直线平行当且仅当两方程的一次项系数成比例, 但与常数项不成比例; 两直线重合当且仅当两方程的所有系数成比例.
• 正交标架下, 直线 `l: A x + B y + C = 0`, `P_0(x_0,y_0) in l`. 当 `B != 0` 时, `(y-y_0)/(x-x_0)` 为一常数 `k`, 称为 `l` 的斜率. 斜率存在的充要条件是直线与 `y` 轴不平行 (或重合). 类似地, `A != 0` 时, `(x-x_0)/(y-y_0)` 为一常数 `m`, 称为 `l` 的 `x`-斜率, 显然 `k, m` 都存在时, 有 `k m = 1`.
• 斜率存在时, 两直线垂直当且仅当 `k_1 k_2 = -1`, 两直线平行或重合当且仅当 `k_1 = k_2`, 两直线相交当且仅当 `k_1 != k_2`.
• 直线方程小集. 约定 `P = (x,y,z)`, `varphi(P) = A x + B y`, `f(P) = varphi(P) + C`.

  	条件	直线 `l` 的方程
  参数方程	`P_0 in l`, `bm r_1 //// l`, `bm r_1 != bb 0`	`P = P_0 + t bm r_1`, `t in RR`
  点向式	`P_0(x_0,y_0) in l`, `bm r_1 = (x_1,y_1) //// l`, `bm r_1 != bb 0`	`|x-x_0,y-y_0; x_1,y_1| = 0`
  两点式	不重合的两点 `(x_i,y_i) in l`, `i = 1,2`	`|x,y,1; x_1,y_1,1; x_2,y_2,1| = 0`
  截距式	`(a,0)`,`(0,b) in l`, `a, b != 0`	`x/a + y/b = 1`
  点斜式	`P_0(x_0,y_0) in l`, `l` 的斜率为 `k`	`y-y_0 = k(x-x_0)`
  斜率式 (y)	`l` 的斜率为 `k`, `(0,b) in l`	`y = k x + b`
  斜率式 (x)	`l` 的 `x`-斜率为 `m`, `(a,0) in l`	`x = m y + a`
  直线束	两直线 `l_i: f_i(P) = 0`, `i = 1, 2` 交于一点, `l` 过其交点	`lambda f_1 + mu f_2 = 0`, `lambda, mu` 不全为零
  一点一直线	`P_0 in l`, `l_0: f(P) = 0 //// l`	`varphi(P-P_0) = 0`
  点法式 (正交标架)	`P_0 in l`, `bm n = (A,B) _|_ l`	`varphi(P-P_0) = 0`

• 设直线 `l: f(P) = 0`, 则平面上全体适合二元一次不等式 `f(P) gt 0` 的点位于直线的同侧, 全体适合 `f(P) lt 0` 的点位于直线的另一侧.
• 设 `bm n` 是直线的一个法向量, `bm n_1 = (bm n)/|bm n|` 是单位法向量, `P_0` 在直线上, 则平面上一点 `P` 在直线上的垂足 `P_1` 满足 `vec(P_1 P) = (vec(P_0 P) * bm n_1) bm n_1`, `P` 到直线的距离为 `|vec(P_1 P)| = |vec(P_0 P) * bm n|`. 特别在正交标架下, 设 `l: A x + B y + C = 0`, 则 `vec(P_1 P) = (A x_P + B x_P + C)(bm n)/|bm n|^2`,
  `|vec(P_1 P)| = |A x_P + B x_P + C|/sqrt(A^2+B^2)`. 正交标架下, 两平面 `A x + B y + C_i`, `i = 1, 2` 的距离等于 `|C_1-C_2|/sqrt(A^2+B^2)`
• 两直线的夹角是指两直线交成的四个角中的任一个, 也指两直线的法向量之间的夹角或其补角. 两平行 (或重合) 直线的夹角等于 `0` 或 `pi`. 正交标架下, 两直线 `A_i x + B_i y + C = 0`, `i = 1,2` 的一个夹角 `theta` 满足 `cos theta = (bm n_1 * bm n_2)/(|bm n_1| |bm n_2|)` `= (A_1 A_2 + B_1 B_2)/(sqrt(A_1^2+B_1^2) sqrt(A_2^2+B_2^2))`.
• 把从 `x` 轴正方向以逆时针旋转到直线方向上的小于 `pi` 的角称为 直线与 `bm x` 轴正方向的夹角或直线的倾斜角, 记为 `alpha`. 正交标架下, 联系斜率的概念, 有 `tan alpha = k`. 记 `Delta x = x_2-x_1`, `Delta y = y_2-y_1`. 直线上从 `(x_1,y_1)` 到 `(x_2,y_2)` 的弦长等于 `(Delta x)/|cos alpha| = sqrt(1+k^2) Delta x` `= (Delta y)/(sin alpha) = sqrt(1+m^2) Delta y`.

平面上直线 `a` 由点 `A` 和方向向量 `bm a` 确定, 直线 `b` 由点 `B` 和方向向量 `bm b` 确定. 若 `bm a, bm b` 不平行, 求两直线的交点 `P`.

在三角形 `ABP` 中使用正弦定理 `|AP| = |AB| (sin B)/(sin P)` `= |vec(AB) xx bm b|/|bm a xx bm b| |bm a|` 用右手法则可以得到: `vec(AP)` 和 `bm a` 同向当且仅当 `vec(AB) xx bm b` 和 `bm a xx bm b` 同向.
有了 `vec(AP)` 的大小和方向, 用 `A` 的坐标加上 `vec(AP)` 就得到 `P` 的坐标.

下面回到空间直线.

直线的线性性质

直线的参数方程和标准方程

取定仿射标架 `{O";" bm d_1, bm d_2, bm d_3}`, 设 `P_0(x_0, y_0, z_0)`, 非零向量 `bm r = (X, Y, Z)`, 则点 `P_0` 和向量 `bm r` 唯一确定了直线 `l`, 使得 `P_0 in l`, `bm r //// l`. 我们有 点 `P` 落在由 `P_0`, `bm r` 确定的直线上当且仅当 `vec(P_0 P), bm r` 线性相关. 由于 `bm r != bb 0`, 所以 `vec(P_0 P)` 可以唯一表示为 `vec(P_0 P) = t bm r`, `t in RR`. 改写得到直线的参数方程 `{ x = x_0 + X t; y = y_0 + Y t; z = z_0 + Z t; :}` `quad`, `t in RR`.

另一方面, 直线 `l` 的方程也可以是 `vec(P_0 P) xx bm r = bb 0`, 即 ` |x-x_0, y-y_0; X, Y| = |y-y_0, z-z_0; Y, Z|` `= |z-z_0, x-x_0; Z, X| = 0`. 约定分母为零时分子也为零, 且 `0/0` 表示任意实数, 则上式化为标准方程或点向式方程: `(x-x_0)/X = (y-y_0)/Y = (z-z_0)/Z`. 这是两个方程联立的方程组. 对任意非零实数 `k`, 称 `kX, kY, kZ` 为直线的方向系数.

直线方程小集

1. 标准方程在可化为普通方程. 不妨令 `X != 0`, 则 `{ (x-x_0)/X = (y-y_0)/Y; (x-x_0)/X = (z-z_0)/Z; :}` 它表示一个平行于或经过 `z` 轴的平面与一个平行于或经过 `y` 轴的平面的交线.
2. 普通方程可化为标准方程. 这只需求出直线的方向向量和直线上一点. 设 `bm r = (X, Y, Z)` 是直线的方向向量, 则 `bm r` 与两平面都平行. 由知, `bm r` 满足方程组 `{ A_1 X + B_1 Y + C_1 Z = 0; A_2 X + B_2 Y + C_2 Z = 0; :}` 代入验证可知 ` bm r = |bm d_1, bm d_2, bm d_3; A_1, B_1, C_1; A_2, B_2, C_2|` 是方程组的解 (行列式中若有相同的两行, 则行列式等于 0). 因为两平面方程的系数不成比例, 所以 `bm r != bb 0`. 为了得到直线上的一点, 不妨设 `|A_1, B_1; A_2, B_2| != 0`, 在两平面的方程中令 `z = 0`, 解关于 `x, y` 的方程组即得.
   在直角坐标系中, 上述过程显得更加直观: 因为 `bm r` 平行于两平面, 所以 `bm r` 垂直于它们的法向量 `bm n_1 = (A_1, B_1, C_1)`, `bm n_2 = (A_1, B_1, C_1)`. 因此可以取 `bm r = bm n_1 xx bm n_2`, 此即上面所取的非零特解.

两直线的相对位置, 直线与平面的相对位置

判断两直线的位置关系 设两直线的参数方程是 `P = P_i + t bm r_i`, `i = 1, 2`. 则
1. 两直线异面当且仅当 `bm r_1, bm r_2, vec(P_1 P_2)` 线性无关;
2. 两直线交于一点当且仅当上面的条件不成立, 且 `bm r_1, bm r_2` 线性无关;
3. 两直线平行但不重合当且仅当上面的条件都不成立, 且 `bm r_1, vec(P_1 P_2)` 线性无关;
4. 两直线重合当且仅当上面各条件都不成立.

	if `(bm r_1, bm r_2, vec(P_1 P_2)) != 0`:
		两直线异面
	elif `bm r_1, bm r_2` 线性无关:
		两直线交于一点
	elif `bm r_1, vec(P_1 P_2)` 线性无关:
		两直线平行, 但不重合
	else:
		两直线重合

判断直线与平面的位置关系 设直线的参数方程是 `P = P_0 + t bm r`, 平面的普通方程是 `f(P) = varphi(P) + D = 0`. 则
1. 直线与平面相交当且仅当 `bm r` 与平面不平行;
2. 直线与平面平行, 但不在平面上当且仅当上面的条件不成立, 且 `P` 不在平面上;
3. 直线在平面上当且仅当上面的条件都不成立.

	if `varphi(bm r) != 0`:
		直线与平面相交
	elif `f(P) != 0`:
		直线与平面平行, 但不在平面上
	else:
		直线在平面上.

杂例

直线 `{A_1 x + B_1 y + C_1 z + D_1 = 0; A_2 x + B_2 y + C_2 z + D_2 = 0 :}` 和平面 `A_3 x + B_3 y + C_3 z + D_3 = 0` 平行或在平面上当且仅当 `|A_1, B_1, C_1; A_2, B_2, C_2; A_3, B_3, C_3| = 0`.

设 `bm r = (X, Y, Z) != bb 0` 是直线的方向向量, 则 `bm r` 与三个平面都平行, 即 `{ A_1 X + B_1 Y + C_1 Z = 0; A_2 X + B_2 Y + C_2 Z = 0; A_3 X + B_3 Y + C_3 Z = 0; :}` 由线性方程组理论, 上面的齐次方程组有非零解当且仅当其系数行列式等于 0.

两直线 `{A_1 x + B_1 y + C_1 z + D_1 = 0; A_2 x + B_2 y + C_2 z + D_2 = 0 :}` 和 `{A_3 x + B_3 y + C_3 z + D_3 = 0; A_4 x + B_4 y + C_4 z + D_4 = 0:}` 有公共点, 则 `|A_1, B_1, C_1, D_1; A_2, B_2, C_2, D_2; A_3, B_3, C_3, D_3; A_4, B_4, C_4, D_4| = 0`.

考虑关于变元 `t_1, t_2, t_3, t_4` 的齐次线性方程组 `{ A_1 t_1 + B_1 t_2 + C_1 t_3 + D_1 t_4 = 0; A_2 t_1 + B_2 t_2 + C_2 t_3 + D_2 t_4 = 0; A_3 t_1 + B_3 t_2 + C_3 t_3 + D_3 t_4 = 0; A_4 t_1 + B_4 t_2 + C_4 t_3 + D_4 t_4 = 0; :}` 设 `(x, y, z)` 是两直线的公共点, 则 `(x, y, z, 1)` 是此方程组的非零解, 由线性方程组理论, 该方程组有非零解当且仅当其系数行列式等于 0.

与异面直线 `{A_1 x + B_1 y + C_1 z + D_1 = 0; A_2 x + B_2 y + C_2 z + D_2 = 0 :}` 和 `{A_3 x + B_3 y + C_3 z + D_3 = 0; A_4 x + B_4 y + C_4 z + D_4 = 0 :}` 都相交的直线 `l` 的方程具有形式 `{ lambda (A_1 x + B_1 y + C_1 z + D_1) + mu (A_2 x + B_2 y + C_2 z + D_2) = 0; lambda' (A_3 x + B_3 y + C_3 z + D_3) + mu' (A_4 x + B_4 y + C_4 z + D_4) = 0; :}` 其中 `lambda, mu` 不全为零, `lambda', mu'` 不全为零. 即 `l` 可以表为两直线各自确定的平面束中的平面的交.

点, 直线, 平面的度量关系

点到直线的距离

设 `bm r` 是直线的单位方向向量, `P_0` 是直线上的点. 则空间一点 `P` 到直线的距离为 `|vec(P_0 P) xx bm r|`. 即以 `vec(P_0 P), bm r` 为邻边的平行四边形在底边 `bm r` 上的高.

两直线的距离

两直线的距离定义为两直线上的点之间的最短距离. 若两直线 `l_1, l_2` 平行, 则 `l_1` 上一点到 `l_2` 的距离就是 `l_1, l_2` 的距离; 若 `l_1, l_2` 相交或重合, 它们的距离为 0. 下面设 `l_1, l_2` 异面, 称分别与 `l_1, l_2` 垂直相交 (即正交) 的直线为 `l_1, l_2` 的公垂线, 两垂足之间的线段称为公垂线段.

两异面直线的公垂线存在唯一.

设两异面直线 `l_i` 分别经过点 `P_i`, 其方向向量分别为 `bm r_i`, `i = 1, 2`. 因为 `bm r_1, bm r_2` 不共线, 所以 `bm r_i, bm r_1 xx bm r_2` 不共线, `i = 1, 2`. 设直线 `l_i` 与 `bm r_1 xx bm r_2` 确定平面 `pi_i`, `i = 1, 2`. 考虑两平面的法向量 `bm n_i = bm r_i xx (bm r_1 xx bm r_2)`, `i = 1, 2`, 我们有 ` bm n_1 xx bm n_2 = ((bm r_1 * bm r_2) bm r_1 - |bm r_1|^2 bm r_2) xx (|bm r_2|^2 bm r_1 - (bm r_1 * bm r_2) bm r_2)` `= (|bm r_1|^2 |bm r_2|^2 - (bm r_1 * bm r_2)^2) bm r_1 xx bm r_2 = |bm r_1 xx bm r_2|^2 bm r_1 xx bm r_2`. 于是 `bm n_1 xx bm n_2 != bb 0`, 即两个法向量不共线. 所以 `pi_1, pi_2` 相交, 设它们的交线为 `l`. 联系的 2, `bm n_1 xx bm n_2` 是 `l` 的方向向量. 故 `bm r_1 xx bm r_2` 也是 `l` 的方向向量, 这说明 `l` 与 `l_1, l_2` 都垂直. 由于 `l, l_i sub pi_i`, 所以 `l` 与 `l_i` 相交, `i = 1, 2`. 故 `l` 是 `l_1, l_2` 的公垂线. 由于平面 `pi_1, pi_2` 及其交线都是唯一确定的, 所以上述证明过程得到的公垂线是唯一的.

设两异面直线 `l_i` 分别经过点 `P_i`, 其方向向量分别为 `bm r_i`, `i = 1, 2`. 则它们的距离等于其公垂线段长, 即 `|(vec(P_1 P_2)"," bm r_1"," bm r_2)| / |bm r_1 xx bm r_2|`. 这个公式说明, 两异面直线的距离等于以 `vec(P_1 P_2), bm r_1, bm r_2` 为棱的平行六面体的体积与以 `bm r_1, bm r_2` 的邻边的平行四边形的面积之比.

1. 先证两异面直线上的点之间的所有连线中, 以公垂线段最短. 设 `l_1, l_2` 的公垂线段为 `M_1 M_2`, 其中 `M_i in l_i`, `i = 1, 2`. 作出由 `P_1, bm r_1, bm r_2` 决定的平面 `pi`, 则 `M_1 M_2` 垂直于 `pi`. 设 `N` 是 `P_2` 在 `pi` 上的垂足. 由 `l_2 //// pi` 知 `|P_2 N| = |M_1 M_2|`. 由于 `|P_2 N|` 是 `P_2` 到 `pi` 的最短距离, 所以 `|M_1 M_2| = |P_2 N| le |P_1 P_2|`.
2. 易知 `bm r_0 = (bm r_1 xx bm r_2)/|bm r_1 xx bm r_2|` 是平面 `pi` 的一个单位法向量, 于是 `|M_1 M_2| = |P_2 N| = |vec(P_1 P_2) * bm r_0|`.

两直线所成的角, 直线和平面所成的角

两直线所成的角规定为它们方向向量夹角中不大于 `pi//2` 的那一个. 直线与平面所成的角规定为直线和直线在平面上的射影所成的角. 当直线与平面垂直时, 它们的夹角规定为 `pi//2`.

包络线

曲线族的包络 设 `gamma` 是平面曲线, 若它与曲线族 `Gamma` 中的每一条曲线 `gamma_t in Gamma` 都相切, 则称 `gamma` 是 `Gamma` 的一条包络线. 若包络线 `gamma` 存在, 且在 `(x(t), y(t))` 处与 `gamma_t: F(x, y, t) = 0` 相切, 则可以证明 `gamma` 满足下面的方程组: `{ F(x, y, t) = 0; F_t(x, y, t) = 0 :}` 视 `t` 为参数, 从方程组中解出 `x(t), y(t)`, 则得到参数方程. 另一方面, 消去参数 `t` 也可以得到隐方程. 这个方程组确定的曲线称为 `t`-检验曲线.
特别当 `Gamma` 为直线族时, 设 `F(x, y, t) = f(t) x + g(t) y - h(t)`, `t`-检验曲线为 `{ f(t) x + g(t) y = h(t); f'(t) x + g'(t) y = h'(t) :}` 这是线性方程组, 我们可以轻松解得包络线的参数方程.

1. 设 `gamma` 的参数方程为 `(x(t), y(t))`. 由题设 `gamma` 在 `(x(t), y(t))` 处的切向量与 `gamma_t` 的切向量平行, 即与 `gamma_t` 的法向量垂直: `F_x x'(t) + F_y y'(t) = 0`. 又 `(x(t), y(t))` 落在 `gamma_t` 上, 有 `F(x(t), y(t), t) = 0`. 这是 `t`-检验曲线的第一个方程. 两边对 `t` 求导得 `F_x x'(t) + F_y y'(t) + F_t = 0`. 上式与 比较得 `F_t = 0`. 这是 `t`-检验曲线的第二个方程.
2. `t`-检验曲线的几何解释: 假设函数 `F` 和 `F_t` 都可微, 把 `F(x, y, t) = 0` 和 `F_t(x, y, t) = 0` 看作 `RR^3` 中的曲面, 它们的交线是空间曲线 `gamma^3`. 联立消去 `t` 后, 得到平面曲线 `gamma`. 这里 `gamma` 是 `gamma^3` 在 `xOy` 平面的投影. `gamma^3` 的方向向量是两曲面法向量的外积: `grad F xx grad F_t` `= (F_x, F_y, F_t) xx (F_(t x), F_(t y), F_(t t))` `= (F_y F_(t t) - F_t F_(t y), F_t F_(t x) - F_x F_(t t), ...)` 而 `gamma` 的方向向量只需取上式的 `x, y` 分量.
   `gamma` 与 `gamma_t` 在 `(x(t), y(t))` 处是相切的. 这是因为 `t`-检验曲线的第一个方程告诉我们 `F(x(t), y(t), t) = 0`, 说明点 `(x(t), y(t))` 在 `gamma_t` 上; 另一方面 `F_x (F_y F_(t t) - F_t F_(t y)) + F_y (F_t F_(t x) - F_x F_(t t))` `= F_t (F_y F_(t x) - F_x F_(t y))`, `t`-检验曲线的第二个方程告诉我们 `F_t(x(t), y(t), t) = 0`, 因此上式在 `(x(t), y(t))` 处等于零. 这说明 `gamma` 的方向向量与 `gamma_t` 的法向量在这一点垂直.

求曲线族 `(x - t)^2 + y^2 = 1` 的包络.

直观上这是一族平移的圆, 它的包络应该是上下两条切线. 列出 `t`-检验曲线: `{ (x-t)^2 + y^2 = 1; 2(t-x) = 0 :}` 由第二式得 `t = x`, 代入第一式得 `y^2 = 1`. 我们同时得到了两条包络线.

求直线族 `1/2 x cos t + y sin t = 1`, `t in [0, 2pi)` 的包络.

列出方程组 `{ 1/2 x cos t + y sin t = 1; -1/2 x sin t + y cos t = 0 :}` 从上式解出 `x, y` 就得到参数方程. 现在我们求隐方程, 两式平方相加得 `x^2/4 + y^2 = 1`, 这是一个椭圆.

求椭圆 `(a cos t, b sin t)` 的全体法线组成的直线族及其包络.

1. `bm r = (a cos t, b sin t)`, `bm r' = (-a sin t, b cos t)`, 设 `bm r` 处的法线方程为 `-a x sin t + b y cos t = c`, 代入 `x = a cos t, y = b sin t` 得 `c = (b^2-a^2)sin t cos t`. 于是椭圆的法线族为 `a x sin t - b y cos t = (a^2 - b^2) sin t cos t`, `quad t in [0, 2pi)`.
2. 解线性方程组 `{ a x sin t - b y cos t - (a^2 - b^2) sin t cos t = 0; a x cos t + b y sin t - (a^2 - b^2) cos 2 t = 0 :}` 得到包络线的参数方程: `(x, y) = (a^2 - b^2)((cos^3 t)/a, -(sin^3 t)/b)`.

在平面直角坐标系中, 求直线 `A_k B_k` 的包络线与坐标轴围成图形的面积, 其中 `A_k(0, k/n)`, `B_k((n+1-k)/n, 0)`, `k = 1, 2, cdots, n`.

记 `k/n = t`, 则直线束可以用 `x/(1-t) + y/t = 1`, `quad t in (0, 1)` 来近似. 解方程组 `{x/(1-t) + y/t = 1; x/(1-t)^2 - y/t^2 = 0 :}` 得到 `x = (1-t)^2`, `y = t^2`. 隐方程为 `sqrt x + sqrt y = 1`, 或 `y = 1 - 2 sqrt x + x`. 面积为 `int_0^1 (1 - 2 sqrt x + x) dx` `= 1 - 4/3 + 1/2 = 1/6`.

杂例

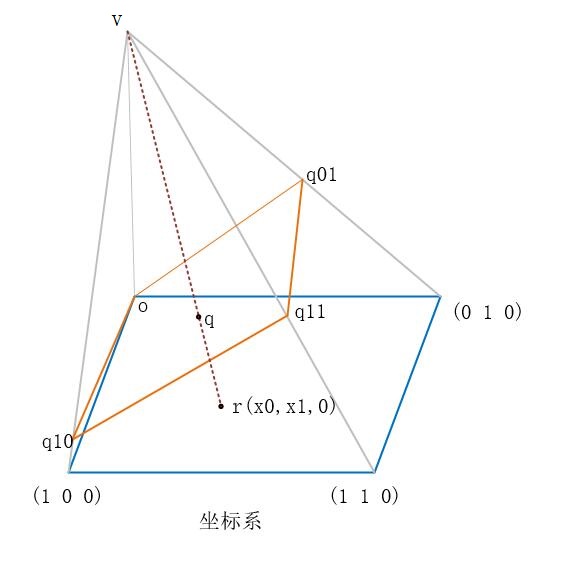
中心投影变换: 平面凸四边形变换为矩形 [来自 机智的小伟] 已知四棱锥的顶点为 `bm v`, 底面为单位正方形 `R`: `bm r_00 = (0, 0, 0)`, `bm r_01 = (0, 1, 0)`, `bm r_10 = (1, 0, 0)`, `bm r_11 = (1, 1, 0)`. 现有一个平面四边形 `Q`, 其中一个顶点与原点重合: `bm q_00 = bm r_00`, 另外三个顶点 `bm q_01`, `bm q_10`, `bm q_11` 分别位于四棱锥的三条棱上. 由于四边形 `Q` 的各顶点共面, 我们设 `bm q_11 = a_0 bm q_10 + a_1 bm q_01`. 这里的 `a_0, a_1` 为已知数.
我们的问题如下: 假设顶点 `bm v` 处有一光源, 使矩形与四边形处于相互射影的关系中, 试确定这个函数关系. 注: 矩形上一点的坐标和四边形上一点的坐标分别用基底表示为 `bm r = x_0 bm r_10 + x_1 bm r_01`,
`bm q = y_0 bm q_10 + y_1 bm q_01`. 于是只需确定 `(x_0, x_1)` 和 `(y_0, y_1)` 之间的函数关系.

1. 四边形的顶点位于棱上的关系写出来就是: `bm r_00 = bm v + t_00 (bm q_00 - bm v)`,
   `bm r_10 = bm v + t_10 (bm q_10 - bm v)`,
   `bm r_01 = bm v + t_01 (bm q_01 - bm v)`,
   `bm r_11 = bm v + t_11 (bm q_11 - bm v)`. 由于 `bm q_00 = bm r_00`, 所以上式的 `t_00 = 1`.
   
2. 假设四边形的法向量为 `bm n`, 于是 `bm q_01 * bm n = bm q_10 * bm n = 0`. 将 的后三个等式与 `bm n` 点乘, 得到 `bm r_10 * bm n = (1 - t_10) bm v * bm n`,
   `bm r_01 * bm n = (1 - t_01) bm v * bm n`,
   `bm r_11 * bm n = (1 - t_11) bm v * bm n`. 但 `bm r_11 = bm r_10 + bm r_01`, 所以 `(1-t_11) = (1-t_10) + (1-t_01)`, 即 `t_11 = t_10 + t_01 - 1`.
3. 下面我们解出系数 `t_00` 到 `t_11`. 先把 的后三个等式改写为 `bm r_10 = (1 - t_10) bm v + t_10 bm q_10`,
   `bm r_01 = (1 - t_01) bm v + t_01 bm q_01`,
   `bm r_11 = (1 - t_11) bm v + (t_10 + t_01 - 1) (a_0 bm q_10 + a_1 bm q_01)`. 由 `bm r_10 + bm r_01 = bm r_11` 和 `(1-t_11) = (1-t_10) + (1-t_01)`, 得到 `t_10 bm q_10 + t_01 bm q_01 = (t_10 + t_01 - 1) (a_0 bm q_10 + a_1 bm q_01)`. 让 `bm q_10` 和 `bm q_11` 的系数分别相等, 有 `t_10 = (t_10 + t_01 - 1) a_0`,
   `t_01 = (t_10 + t_01 - 1) a_1`. 解这个二元一次方程组, 得到 `t_00 = 1`, `quad t_10 = a_0//(a_0 + a_1 - 1)`, `quad t_01 = a_1//(a_0 + a_1 - 1)`, `quad t_11 = 1//(a_0 + a_1 - 1)`.
4. 最后, 来确定矩形与四边形之间的射影关系. 由共线关系得到 `x_0 bm r_10 + x_1 bm r_01`
   `= bm r = (1-t) bm v + t bm q`
   `= (1-t) bm v + t (y_0 bm q_10 + y_1 bm q_01)`
   `= (1-t) bm v + (t y_0)/t_10 (bm r_10 - (1-t_10) bm v) + (t y_1)/t_01 (bm r_01 - (1-t_01) bm v)`
   由于 `bm r_10, bm r_01, bm v` 线性无关, 可以让它们的系数分别相等, 有 `x_0 = (t y_0)/t_10`, `quad x_1 = (t y_1)/t_01`, `quad 0 = (1-t) - (t y_0)/t_10 (1-t_10) - (t y_1)/t_01(1-t_01)`. 第三式改写为 `t = 1 - x_0 (1-t_10) - x_1 (1-t_01)`, 代入前两式得 `(y_0, y_1) = ((t_10 x_0, t_01 x_1))/(1 - x_0 (1-t_10) - x_1 (1-t_01))`. 再将 `t_10, t_01` 的值代入, 最终得到 `(y_0, y_1) = ((a_0 x_0, a_1 x_1))/(a_0 + a_1 - 1 + (1 - a_1) x_0 + (1 - a_0) x_1)`. 其逆变换为 `(x_0, x_1) = ((a_1(a_0+a_1 - 1) y_0, a_0(a_0 + a_1 - 1)y_1))/(a_0 a_1 + a_1 (a_1 - 1) y_0 + a_0 (a_0 - 1) y_1)`.