[来自《射影几何入门》]
我们的讨论将在射影平面 `P(RR^2)` 和射影空间 `P(RR^3)` 中进行. 射影平面和欧氏平面 `RR^2` 的区别在于, 它比 `RR^2` 多了无穷远点和无穷远直线的概念.
在 `RR^2` 上考虑直线 `l` 和直线外一点 `P`. 我们把过 `P` 的全体直线组成的直线束仍记为 `P`. 任取 `Q in l`, 则点 `Q` 完全决定了直线束中的一条直线 `PQ`. 然而直线束中有一条直线在 `l` 上找不到对应的点, 那就是与 `l` 平行的那条直线. 为弥补这个缺憾, 我们规定这条直线与 `l` 上的无穷远点对应, 从而在直线 `l` 与线束 `P` 之间建立了双射, 这个双射就称为直线与线束间的透视对应, 我们称这样的直线与线束是相互透视的.
注意, 要使双射成立, 我们引入的直线 `l` 的无穷远点必须唯一, 即不论向直线的哪个方向走到「尽头」, 最终都会到达同一个无穷远点. 为 `RR^2` 上的每条直线都引入一个无穷远点, 最后, 再规定所有这些无穷远点组成一条无穷远直线. 这样一来, 我们可以说, 射影平面上任意两条不同直线有唯一的交点; 特别地, 两条平行直线相交于无穷远点, 直线与无穷远直线的交点是它的无穷远点.
若干透视对应的复合称为射影对应, 比如平面上有多个直线与线束, 其中 `l_1` 与 `S_1` 透视, `S_1` 与 `l_2` 透视, `l_2` 又与 `S_3` 透视..., 那么所有这些直线与线束都是相互射影的.
射影平面上的直线又称为点列, 这个名字强调了直线是点的集合.
再看射影空间 `P(RR^3)`. 我们为 `RR^3` 的每条直线都引入一个无穷远点, 这些无穷远点全体组成一个无穷远平面. 无穷远平面和另一个平面的交点组成后者的无穷远直线. 于是, `P(RR^3)` 中任意两个不同平面有唯一的交线; 特别地, 两平行平面相交于无穷远直线. `P(RR^3)` 中直线与平面有唯一的交点; 当直线与平面平行时, 它们相交于直线的无穷远点. `P(RR^3)` 中两条不同直线有 0 或 1 个交点; 两平行直线相交于无穷远点, 两异面直线的无穷远点不相同, 因而没有交点.
我们专门讨论 `P(RR^2)` 的四种可视化.

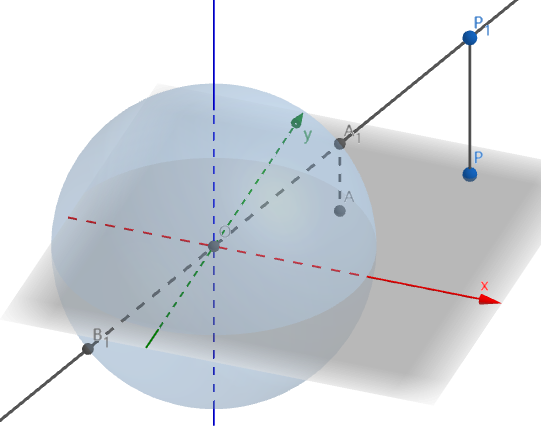
在 `RR^3` 中, 将 `xOy` 平面上一点 `P(x, y, 0)` 抬升到 `P_1(x, y, 1)`, 它唯一确定了线束 `O` (即, 通过原点的全体直线) 中的一条直线 `l = OP_1`:
`RR^2 to 线束 O`
`(x, y) mapsto l: OP_1`.
与平面上的无穷远点对应的, 是线束 `O` 中位于平面 `xOy` 上的那些直线, 这些直线与平面 `z = 1` 平行, 无法用刚才的几何方法得到.
在线束模型中, 线束 `O` 代表射影空间 `P(RR^2)`, 线束 `O` 中的一条直线代表 `P(RR^2)` 中的一点.
在线束模型中, 取线束 `O` 中直线 `l` 与单位球面 `S^1` 的交点 `A_1, B_1`, 得到映射
`RR^2 to S^1`
`(x, y) mapsto +-(x, y, 1) // sqrt(x^2 + y^2 + 1)`.
每条直线与 `S^1` 有两个交点, 它们位于一条直径的两端, 称为一组对径点.
我们把这两点等同起来, 代表射影空间 `P(RR^2)` 中的同一点.
与无穷远点对应的, 是 `S^1` 赤道 (即它与 `xOy` 平面相交的部分, 平面 `xOy` 上的单位圆) 上的点,
在球面模型中, 单位球面上的全体对径点代表射影空间 `P(RR^2)`, 每组对径点代表 `P(RR^2)` 中的一点.
在球面模型中, 我们只取对径点 `A_1, B_1` 中 `z ge 0` 的那一个 (`A_1`), 得到映射
`RR^2 to S^1_(z ge 0)`
`(x, y) mapsto (x, y, 1) // sqrt(x^2 + y^2 + 1)`.
这样除了赤道外, `RR^2` 中的点与上半球面的点一一对应. 而赤道上和球面模型相同:
每组对径点对应一个无穷远点.
把半球模型「拍平」到单位圆盘 `D^2` 中, 得到映射
`RR^2 to D^2`
`(x, y) mapsto (x, y) // sqrt(x^2 + y^2 + 1)`.
`RR^2` 中的点与 `D^2` 的内点一一对应. 而 `D^2` 边界上的每组对径点对应一个无穷远点.
本节对射影空间的四种可视化仅用于说明射影空间定义的合理性, 并帮助理解射影空间的结构. 在以下的叙述与插图中, 为直观起见, 我们通常仍使用 `RR^2` 的视角来描绘射影空间, 并想象它在无穷远处有一条直线.
Desargues (笛沙格) 定理 对两个三角形 `ABC` 和 `A'B'C'`, 设 `A B nn A'B' = P`, `B C nn B'C' = Q`, `C A nn C'A' = R`, 则有 `A A'`, `B B'`, `C C'` 三线共点 `iff` `P, Q, R` 三点共线.
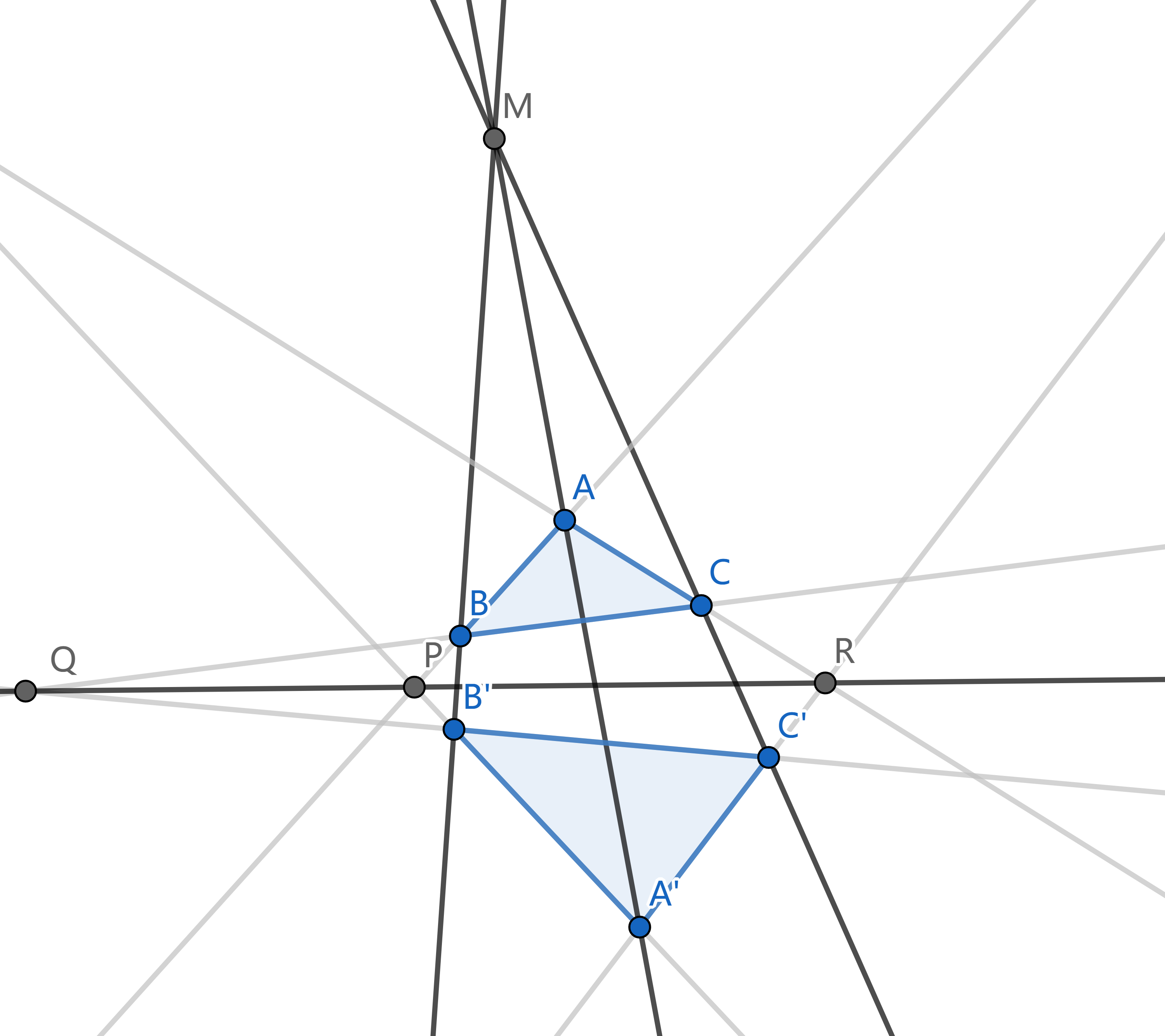
完全四边形 在平面上, 连接四边形的两条对角线, 这两条直线连同原来的四条边一共 6 条直线, 组成的图形称为完全四边形. 或者, 将平面上四点两两连接得到的图形就叫做完全四边形. 完全四边形共有三组对边: 除了原四边形的两组对边外, 我们把两条对角线也看作一组对边.
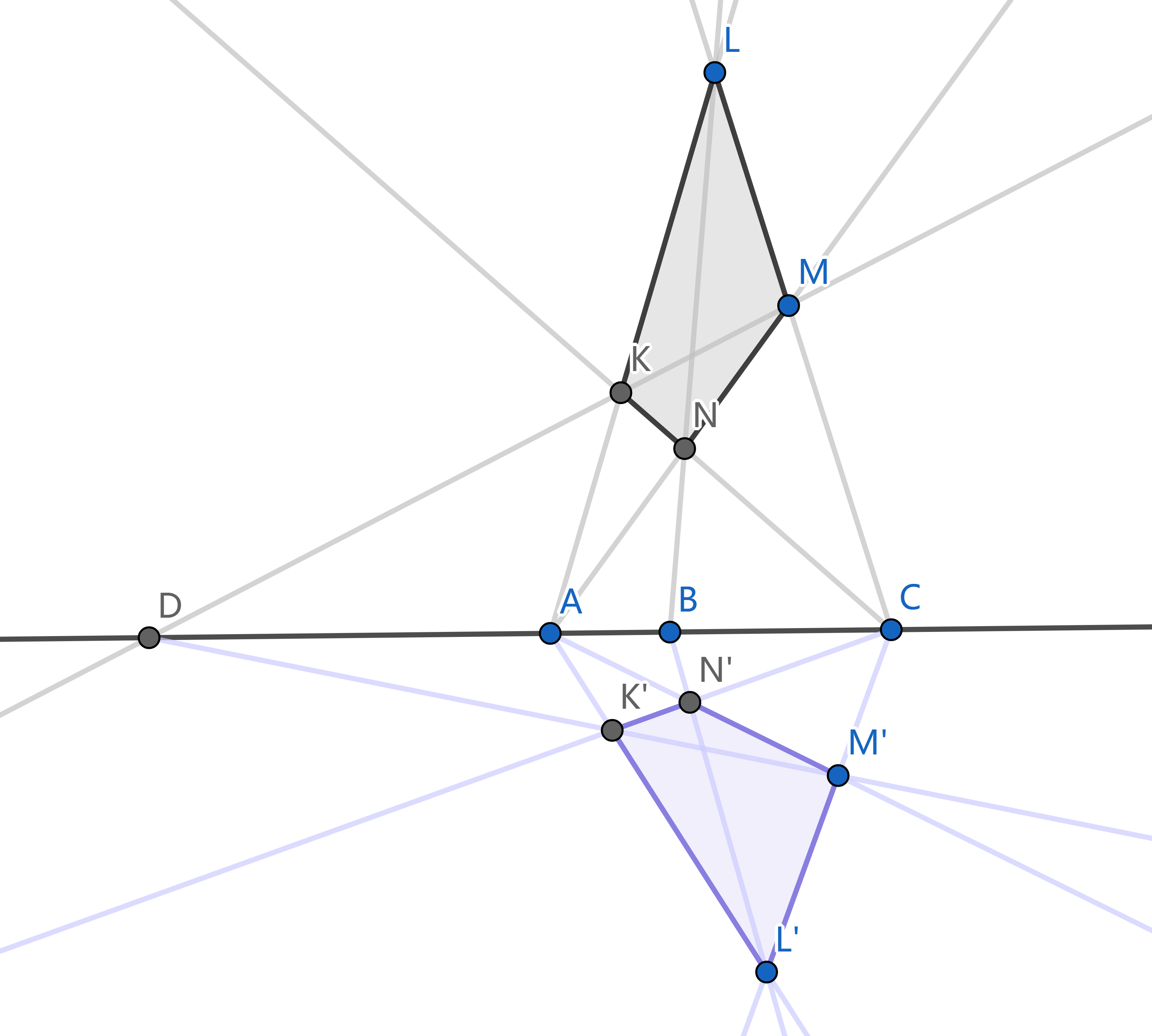
四调和点定理表明, 在直线上任取 `A, B, C` 三点, 可以作出一点 `D`, 它的位置完全由 `A, B, C` 的位置决定. 我们称这样的四点 `A, B, C, D` 为四调和点. 由于定理的叙述中 `B, D` 两点位置对等, 我们也称 `B, D` 关于 `A, C` 调和共轭, 或者称 `B, D` 两点调和分割线段 `AC`.
调和共轭的对称性 如果 `B, D` 关于 `A, C` 调和共轭, 则 `A, C` 也关于 `B, D` 调和共轭.
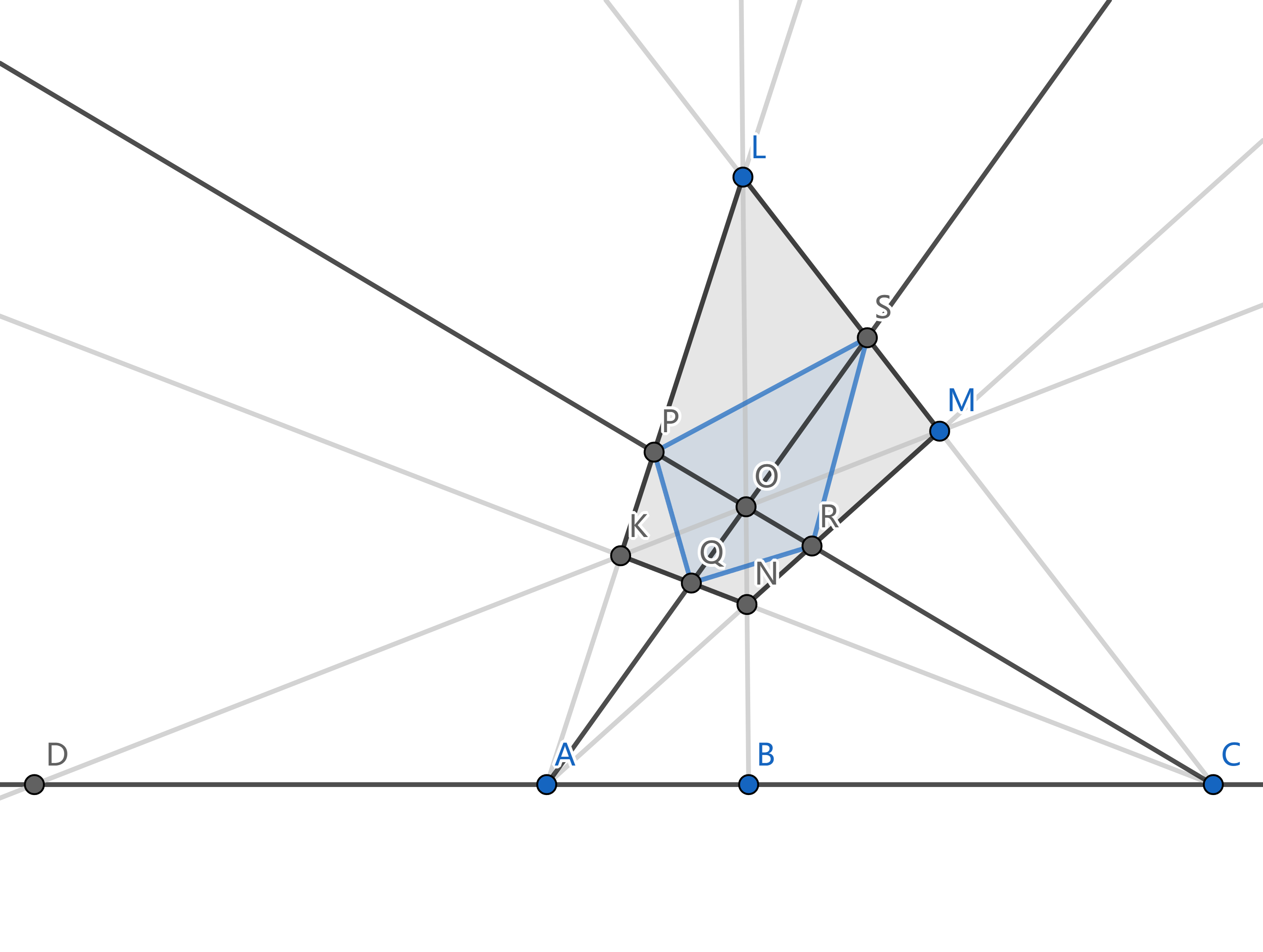
设 `B, D` 关于 `A, C` 调和共轭, 相应的完全四边形是 `KLMN`. 记对边 `KM`, `LN` 的交点为 `O`, 连接 `AO`, `CO`, 这两条直线把四边形 `KLMN` 分为四个四边形. 我们看其中的一个 `KPOQ`, 它的一组对边 `PK`, `OQ` 通过点 `A`, 另一组对边 `PO`, `KQ` 通过点 `C`, 又 `KO` 通过点 `D`, 于是由 `B, D` 关于 `A, C` 调和共轭知, `PQ` 过点 `B`. 考察其它三个小四边形, 同理得 `SR` 过点 `B`, `PS`, `QR` 过点 `D`. 现在, 完全四边形 `PQRS` 的一组对边过点 `B`, 另一组对边过点 `D`, 其剩下的一组对边分别过 `A, C`. 这说明 `A, C` 关于 `B, D` 调和共轭.
四调和点的射影不变性 设直线 `l` 上的 `A, B, C, D` 为四调和点, 将 `l` 射影对应到直线 `l'`, 则对应点 `A', B', C', D'` 也是四调和点.
如图, 线束