[知乎@杨树森]
张量 (tensor) 是向量、矩阵的自然推广. 粗略地说, 向量是一阶张量,
矩阵是二阶张量. 一般地, `n` 阶张量是一个 `n` 重线性函数
`f: (V^ast)^p xx V^q to RR`,
`(u_1, cdots, u_p, v^1, cdots, v^q) mapsto x`,
其中 `p+q=n`, `v^1, cdots, v^q` 是线性空间 `V` 中的元素,
而 `u_1, cdots, u_p` 是对偶空间 `V^ast` 中的元素.
多维数组的概念可以参考 C 语言之类的编程语言. 一个形状为 `N_1 xx cdots xx N_n` 的多维数组写作 `a[N_1]cdots[N_n]`, 它可以看作一个 `n` 元函数 `a(i_1, cdots, i_n)`, 其中第 `k` 个下标 `i_k` 的取值范围是 `1, cdots, N_k`. 设有多维数组 `a[N_1]cdots[N_n]` 和 `b[M_1]cdots[M_m]`, 规定它们之间的乘法 (张量积) 如下: `a : b = c[N_1]cdots[N_n][M_1]cdots[M_m]`, 其中 `c(i_1, cdots, i_n, j_1, cdots, j_m) = a(i_1, cdots, i_n) b(j_1, cdots, j_m)`. 这就是说, `n` 维数组和 `m` 维数组的乘积是一个 `n+m` 维数组, 且这个数组 `c` 的前 `n` 个下标由 `a` 贡献, 后 `m` 个下标由 `b` 贡献.
[ 1*[3, 4], 2*[3, 4] ] = [ [1*3, 1*4], [2*3, 2*4] ] = [ [3, 4], [6, 8] ].
[
[3, 4],
[6, 8]
] : [5, 6, 7]
= [
[3, 4] : [5, 6, 7],
[6, 8] : [5, 6, 7]
]
= [
[
[3*5, 3*6, 3*7],
[4*5, 4*6, 4*7],
],
[
[6*5, 6*6, 6*7],
[8*5, 8*6, 8*7]
]
].
特别地, 两个一维数组的乘积又称为并矢. 如 `bm a = (a_1, a_2, a_3)`,
`bm b = (b_1, b_2, b_3)`, 则
`bm a : bm b`
`= [a_1; a_2; a_3] [b_1, b_2, b_3]`
`= [a_1 b_1, a_1 b_2, a_1 b_3;
a_2 b_1, a_2 b_2, a_2 b_3;
a_3 b_1, a_3 b_2, a_3 b_3
]`.
注意这里的矩阵记号 `[a, b; c, d]` 是多维数组 [[a, b], [c, d]]
的简写. 不引起混淆的情况下, 并矢也可以简记为 `bm a bm b`.
下面讨论的线性空间默认为 `bbb F` 上的有限维空间.
线性空间 `V` 上全体线性函数构成一个线性空间, 称为 `V` 的对偶空间 `V^ast`.
对偶空间中加法与数乘的定义是
`(f + g)(x) = f(x) + g(x)`,
`(k f)(x) = k f(x)`.
对偶空间与原空间同构, 但同构映射依赖基的选取.
设 `e_1, cdots, e_n` 是 `V` 的一组基, 则线性函数 `f_1, cdots, f_n` 是 `V^ast` 的一组基, 其中 `f_i(e_j) = delta_(i j)`, 且任意 `f in V^ast` 在这组基下的坐标为 `(f(e_1), cdots, f(e_n))`. 这组基称为对偶基, 见下文. 同构映射为 `varphi := sum k_i e_i mapsto sum k_i f_i`.
自然同构 对偶空间的对偶空间与原空间同构, 且同构映射 `varphi := bm v mapsto f mapsto f(bm v)` 不依赖基的选取.
`V^ast` 中的元素, 即 `V` 上的线性函数称为 `V` 的协变, `V^(ast ast)` 中的元素, 即 `V^ast` 上的线性函数称为 `V` 的逆变或反变. 根据自然同构 `V^(ast ast) cong V`, 也可以认为逆变就是 `V` 中的向量.
今后我们不再区分 `V^(ast ast)` 与 `V`.
对偶基 设 `{v_i}_(i=1)^n` 是线性空间 `V` 的一组基, `{v_i^ast}_(i=1)^n` 是其对偶空间 `V^ast` 的一组基. 如果满足 `v_i^ast(v_j) = delta_(i j)`, `quad i, j = 1, cdots, n`, 则称 `{v_i^ast}` 是 `{v_i}` 的对偶基.
设 `{u_i}`, `{v_i}` 是 `V` 的两组基, `{u_i^ast}`, `{v_i^ast}` 是相应的对偶基, 线性变换 `cc A, cc B` 满足 `cc A u_i = v_i`, `cc B u_i^ast = v_i^ast`. `cc A, cc B` 在基底 `{u_i}` 下的表示矩阵记为 `bm A, bm B`, 则 `bm B^(sf T) bm A = bm I`.
由对偶基定义,
`u_i^ast(u_j) = delta_(i j) = v_i^ast(v_j)`,
由表示矩阵定义,
`(v_1, cdots, v_n) = (u_1, cdots, u_n) bm A`,
`(v_1^ast, cdots, v_n^ast) = (u_1^ast, cdots, u_n^ast) bm B`.
用 `a_(i j)`, `b_(i j)` 代表矩阵 `bm A, bm B` 的元素, 计算得
`delta_(i j) = v_i^ast(v_j)`
`= (sum_k u_k^ast b_(k i))(sum_l u_l a_(l j))`
`= sum_(k, l) b_(k i) a_(l j) delta_(k l)`
`= sum_k b_(k i) a_(k j)`,
即 `bm B^(sf T) bm A = bm I`.
张量形式的证明.
`bm e_j = a_j^i bm x_i`,
`bm e^j = b_i^j bm x^i`.
于是
`delta_i^j = bm e_i * bm e^j`
`= a_i^k b_l^j (bm x_k * bm x^l)`
`= a_i^k b_l^j delta_k^l`
`= a_i^k b_k^j`.
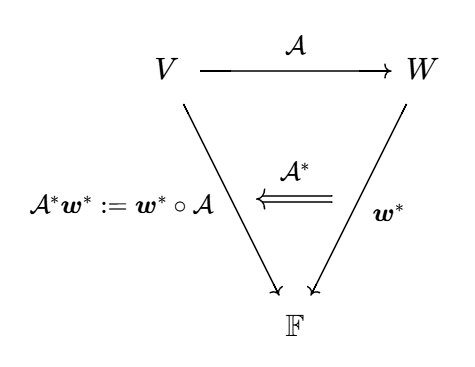
对偶线性映射 设 `cc A` 是线性空间 `V` 到 `W` 的线性映射, 定义它的对偶映射 `cc A^ast` 是 `W^ast` 到 `V^ast` 的线性映射: `cc A^ast := bm w^ast mapsto bm w^ast @ cc A`. 映射 `cc A^ast` 也称为一个拉回, 因为它把 `W to bbb F` 的映射拉回到 `V to bbb F`. 对偶线性映射的合成满足 `cc (A B)^ast = cc B^ast cc A^ast`.

对偶映射的矩阵 设 `cc A in "Hom"(V, W)`, `cc A^ast` 是它的对偶映射. 设线性映射 `cc A` 在特定基底下的矩阵为 `bm A`, 则对偶映射 `cc A^ast` 在对偶基下的矩阵为 `bm A^(sf T)`.
设 `cc A` 在 `V, W` 的基底 `{v_i}`, `{w_j}` 下的矩阵为 `bm A`, 即
`cc A v_i = sum_j A_i^j w_j`.
又设 `cc A^ast` 在对偶基底 `{v_i^ast}`, `{w_j^ast}` 下的矩阵为 `bm B`, 即
`cc A^ast w_i^ast = sum_j B_i^j v_j^ast`.
于是
`(cc A^ast w_i^ast) v_k`
`= sum_j B_i^j v_j^ast v_k`
`= sum_j B_i^j delta_(j k)`
`= B_i^k`,
`(w_i^ast @ cc A) v_k`
`= sum_j A_k^j w_i^ast w_j`
`= sum_j A_k^j delta_(i j)`
`= A_k^i`.
由 `cc A^ast w_i^ast = w_i^ast @ cc A` 得到 `B_i^k = A_k^i`.
设 `V_1, cdots, V_p` 是 `p` 个线性空间, 维数分别是 `n_1, cdots, n_p`. 如果 `f: V_1 xx cdots xx V_p to RR` 关于它的每个分量都是线性函数, 则称它是多重线性函数. `V_1 xx cdots V_p` 上全体多重线性函数的集合记为 `cc L(V_1, cdots, V_p"; "RR)`, 它是一个线性空间.
任取这 `p` 个线性的空间的基底
`(e_1^((1)), cdots, e_(n_1)^((1)))`,
`cdots`,
`(e_1^((p)), cdots, e_(n_p)^((p)))`.
从集合 `cc L(V_1, cdots, V_p"; "RR)` 中取 `n_1 cdots n_p` 个元素
`f_(i_1 cdots i_p)`, `quad i_k in {1, cdots, n_k}`.
其中 `f_(i_1 cdots i_p)` 将多重基向量 `(e_(i_1)^((1)), cdots,
e_(i_p)^((p)))` 映为 `1`, 其它多重基向量映为 `0`.
可以验证这些 `f_(i_1 cdots i_p)` 就构成 `cc L(V_1, cdots, V_p"; "RR)`
的基底.
从以上证明看出, 在有限维的情形, 多重线性函数的坐标就形如多维数组, 它的坐标运算就是多维数组的运算.
线性空间 `V` 上的 `{::}_p^q` 型张量是指如下的 `p+q` 重线性函数: `f: (V^ast)^p xx V^q to RR`, 其中 `p+q` 称为 `f` 的阶数, `p` 称为协变阶数, `q` 称为逆变或反变阶数. `V` 上全体 `{::}_p^q` 型张量的集合记为 `V_p^q`.
根据自然同构, `V` 上的 `{::}_p^q` 型张量也可看作 `V^ast` 上的 `{::}_q^p` 型张量, 或者看作 `f: V^q to V^p`.
张量的坐标表示 `V` 上的 `{::}_p^q` 型张量在基底下写成 `f = sum_(i_1 cdots i_p j_1 cdots j_q) k_(i_1 cdots i_p)^(j_1 cdots j_q) f_(i_1 cdots i_p)^(j_1 cdots j_q)`. 上式共有 `n^(p+q)` 项相加. 其中系数 `k_(i_1 cdots i_p)^(j_1 cdots j_q)` 称为这个张量的分量; 张量的分量形如一个多维数组. `p+q` 重基函数 `f_(i_1 cdots i_p)^(j_1 cdots j_q)` 将 `q` 重基向量 `(e_(j_1), cdots, e_(j_q))` 映到 `p` 重基向量 `(e_(i_1), cdots, e_(i_p))`, 而将其它 `q` 重基向量映为零 (`p` 重零向量). 特别 `p = 0` 时, `p` 重基向量 `(e_(i_1), cdots, e_(i_p))` 退化为 `1`.
张量观点下欧氏空间的内积运算 在标准正交基 `bm e_1, cdots, bm e_n` 下, 两向量的内积 `bm x * bm y` `= (sum_i x_i bm e_i) * (sum_j y_j bm e_j)` `= sum_(i j) x_i y_j bm e_i * bm e_j` `= sum_(i j) x_i y_j delta_(i j)`. 内积运算 `f(bm x, bm y) = bm x * bm y` 接收两个 `RR^n` 中向量, 输出一个实数, 它是欧氏空间 `RR^n` 上的二阶协变张量. 其分量 `delta_(i j)` 恰为单位矩阵.
张量观点下的线性变换 线性变换 `f(bm x) = cc A bm x` 接收一个向量, 输出一个向量, 它是线性空间 `V` 上的 `{::}_1^1` 型张量, 其分量就是 `cc A` 的系数矩阵.
`V` 上全体 `{::}_p^q` 型张量 `V_p^q` 可以分解为线性空间的张量积: `V_p^q = underbrace(V : cdots : V)_p : underbrace(V^ast : cdots : V^ast)_q`.
为便于运算, 我们总是取定一个基底, 然后引入张量的坐标表示. 和矢量一样, 张量与基底的选取无关, 但它的坐标与基底有关. 在不引起混淆的情况下, 我们把张量的坐标表示也称为张量.
"逆天" `rarr` 逆变是上标; "鞋" `rarr` 协变是下标.
Einstein 求和约定的乘积可交换 [群友@乐正垂星] 例如下面的式子成立: `A_i^k B_k^j = B_k^j A_i^k`. 它们作为张量的分量, 只是数字而已, 可以随意交换. 而当我们说矩阵 `A B != B A` 时, 实际上是说 `A^i_k B^k_j != B^i_k A^k_j`, 矩阵次序的交换对应着上下指标的交换.
对称指标与反对称指标缩并结果为零 例如设 `X^(i j)` 对称, `Y_(i j k)` 反对称, 则 `X^(i j) Y_(i j k)` `= -X^(j i) Y_(j i k)`. 但 `i, j` 是哑指标, 可以随意改写为其它字母, 比如把 `i` 重写成 `j`, 而 `j` 重写成 `i`. 因此上式右边等于 `-X^(i j) Y_(i j k)`. 该结果恰比原式多一个负号, 说明原式为零.
向量的叉乘 笛卡尔坐标系中, 若向量 `C = A xx B`, 我们知道它的 `x` 坐标满足 `C_x = A_y B_z - A_z B_y`, 用 Levi-Civita 符号, 就是 `C_c = epsi_(a b c) A^a B^b`.
以 `x` 坐标为例, `y, z` 同理: `C_x = epsi_(a b x) A^a B^b` `= sum_(a, b in {x, y, z}) epsi_(a b x) A^a B^b` 但由于 `epsi` 的反对称性, `a, b` 相等时, 该项为零; `a, b` 等于 `x` 时该项也为零. 故上式等于 `epsi_(y z x) A^y B^z + epsi_(z y x) A^z B^y` `= A^y B^z - A^z B^y`.
逆变、协变的由来
设 `x` 是线性空间 `V` 中的向量, `f` 是 `V` 上的线性函数.
取定 `V` 的基底 `alpha_i` 和 `beta_i`, 有
`x = x^i alpha_i = y^i beta_i`,
`f(x) = x^i f(alpha_i) = y^i f(beta_i)`.
设基底间的过渡矩阵为 `A_i^j`, 即 `beta_i = A_i^j alpha_j`,
则 `f(beta_i) = A_i^j f(alpha_j)`. `f(alpha_j)` 到 `f(beta_i)`
间相差的变换与基底的变换一致, 是协变. 又
`x^j alpha_j = y^i beta_i`
`= y^i A_i^j alpha_j`,
即 `x^j = A_i^j y^i`, 或 `y^i = (A_i^j)^-1 x^j`.
`x^j` 到 `y^i` 间相差的变换与基底的变换相反, 是逆变.
度规 (或度量张量) 定义为基底与对偶基底间的过渡矩阵:
`bm e_i = g_(i j) bm e^j`,
`quad bm e^i = g^(i j) bm e_j`.
于是
`bm e_i * bm e_j = g_(i j) bm e^j * bm e_j = g_(i j)`.
同理 `bm e^i * bm e^j = g^(i j)`.
上式也可以作为度规的定义.
度规矩阵的行列式 `g := det(g_(i j))` 称为 Gauss 曲率.
`bbb E^3` 中, Eddington 张量定义为:
`cc E_(i j k) = bm e_i xx bm e_j * bm e_k`,
`cc E^(i j k) = bm e^i xx bm e^j * bm e^k`,
`cc E_i^(j k) = bm e_i xx bm e^j * bm e^k`.
它在叉积中的作用类似于度规在点积中的作用.
设 `bm u xx bm v = a^l bm e_l = b_l bm e^l`,
分别点乘 `bm e^k` 和 `bm e_k` 得
`a^k = bm u xx bm v * bm e^k = u_i v_j E^(i j k)`,
`b_k = bm u xx bm v * bm e_k = u^i v^j E_(i j k)`.
对偶基底的关系
设 `i, j, k` 是 `1, 2, 3` 的偶排列, 则
由于
`bm e^i * bm e_j = bm e^i * bm e_k = 0`,
`bm e^i * bm e_i = 1 = (bm e_j xx bm e_k * bm e_i)/(bm e_j xx bm e_k * bm e_i)`,
所以
`bm e^i = (bm e_j xx bm e_k)/(bm e_j xx bm e_k * bm e_i)`
`= (bm e_j xx bm e_k)/(bm e_1 xx bm e_2 * bm e_3)`
`= 1/sqrt g (bm e_j xx bm e_k)`,
`bm e_i = (bm e^j xx bm e^k)/(bm e^j xx bm e^k * bm e^i)`
`= (bm e^j xx bm e^k)/(bm e^1 xx bm e^2 * bm e^3)`
`= sqrt g (bm e^j xx bm e^k)`.
`bm e_i = 1/2 E_(i j k) (bm e^j xx bm e^k)`,
`bm e^i = 1/2 E^(i j k) (bm e_j xx bm e_k)`,
`bm e_i xx bm e_j = E_(i j k) bm e^k`,
`bm e^i xx bm e^j = E^(i j k) bm e_k`.
先证第一式. 右边的求和排除掉相同指标后, `j, k` 的取法共有 2 种, 一种使得 `i,
j, k` 是奇排列, 一种使得它是偶排列.
因此右边等于 `sqrt g (bm e^j xx bm e^k) = bm e_i`.
再证第三式. 右边的求和排除掉相同指标后只有一项. 如果 `i, j, k` 是偶排列, 则右边等于
`sqrt g 1/sqrt g (bm e_i xx bm e_j)`.
如果 `i, j, k` 是奇排列, 交换 `i, j` 就化为偶排列的情形.
今后我们常在逆变坐标下进行微分. 张量 `A` 对逆变坐标 `x^i` 的微分 `pp A x^i` 用「逗号下标」的方式简记为 `A,_i`.
标架运动方程
对空间 `RR^3` 中的每一点 `P(x^1, x^2, x^3)` 都建立一个局部标架 `{P";" bm e_i";" bm e^j}`,
`i, j = 1, 2, 3`.
基向量 `bm e_i` 和 `bm e^j` 是 `P` 的坐标 `x^1, x^2, x^3` 的函数, 且满足等式
`bm e_(i, j) = bm e_(j, i)`.
(`ast`)
例如, 当存在二阶连续可微的向量函数 `bm r(x^1, x^2, x^3)`, 使得 `bm r_(,i) = bm e_i` 时,
上式实际上说的是二阶混合偏导可交换: `bm r_(,i j) = bm r_(,j i)`.
我们把基向量对坐标求微分, 得到标架运动方程:
`bm e_(j, i) := Gamma_(i j)^k bm e_k := Gamma_(i j k) bm e^k`.
这里 `Gamma_(i j k)` 和 `Gamma_(i j)^k` 分别叫做第一、二类 Christoffel 符号 (克氏符号).
由假定 (`ast`), 两类克氏符号都关于下标 `i, j` 对称.
它们是标架运动方程中的系数, 称为联络系数.
先证 1. 利用度规定义, `Gamma_(i j k) bm e^k` `= Gamma_(i j)^k bm e_k` `= Gamma_(i j)^l bm e_l` `= Gamma_(i j)^l g_(l k) bm e^k`. 2. 只需在 1. 的两边同乘 `g^(l k)`.
`bm e_(,i)^j = -Gamma_(i k)^j bm e^k = -Gamma_(i j k) bm e_k`. ??
用度规表示克氏符号
`Gamma_(i j k) = 1/2 (g_(i k,j) + g_(j k,i) - g_(i j,k))`,
`Gamma_(i j)^l = 1/2 g^(k l) (g_(i k,j) + g_(j k,i) - g_(i j,k))`.
写出右边各项
`g_(i k,j)`
`= (bm e_i * bm e_k)_(,j)`
`= bm e_(i,j) * bm e_k + bm e_i * bm e_(k,j)`,
`g_(j k,i)`
`= bm e_(j,i) * bm e_k + bm e_j * bm e_(k,i)`,
`g_(i j,k)`
`= bm e_(i,k) * bm e_j + bm e_i * bm e_(j,k)`.
利用 `bm e_(i,j) = bm e_(j,i)` 有
`g_(i k,j) + g_(j k,i) - g_(i j,k)`
`= 2 bm e_(i,j) * bm e_k`
`= Gamma_(i j)^l bm e_l * bm e_k`
`= Gamma_(i j)^l g_(k l)`
`= Gamma_(i j k)`.
两边同乘 `g^(k l)` 即得第二条公式.