从勾股数到 Fermat 大定理

勾股数

由熟知的勾股定理 (Pythagorean theorem), 直角三角形的三边长 `a, b, c` 满足 `a^2+b^2=c^2`. 我们称满足上述不定方程的正整数 `a, b, c` 为一组勾股数 (Pythagorean triple), 如 `3, 4, 5`; `5, 12, 13`; `7, 24, 25` 等. 以勾股数为边长的直角三角形叫勾股三角形. 注意到像 `3, 4, 5` 与 `6, 8, 10` 是本质相同的勾股数, 故定义勾股数 `a, b, c` 是本原的, 如果 `gcd(a, b, c) = 1`.

本原勾股数 `a, b, c` 两两互素, 且 `c` 为奇数, `a, b` 一奇一偶.

设 `d = (a, b)`, 则 `d^2 | a^2 + b^2 = c^2`, 这推出 `d | c`. 于是 `d | (a, b, c) = 1`, 即 `d = 1`. 同理 `(b, c) = (c, a) = 1`.
因为 `(a, b, c)` 两两互素, 它们中的偶数不超过一个, 假设 `c` 为偶数, 则 `a, b` 为奇数. 设 `a = 2m+1`, `quad b = 2n+1`, `quad c = 2k`, 则 `a^2 + b^2 -= 2 (mod 4)`, `c^2 -= 0 (mod 4)`, 矛盾. 因此 `c` 为奇数. 注意到 `a, b` 不全为偶数, 其中一个为奇数, 则另一个为偶数.

由于 `a, b` 地位对称, 不妨设 `b` 是偶数, 则本原勾股数的全体可以表示为 `a = u^2-v^2`, `quad b = 2u v`, `quad c = u^2+v^2`. 其中 `u gt v gt 0`, `quad (u, v) = 1`, 且 `u, v` 一奇一偶.

容易说明满足上述条件的 `(a, b, c)` 确实是本原勾股数. 下证必要性. 注意 `c-a, c+a, b` 都是正的偶数, 可设 `2A = c-a`, `quad 2B = b`, `quad 2C = c+a`, `A, B, C` 为正整数. 因为 `b^2 = c^2 - a^2 = (c-a)(c+a)`, 我们有 `B^2 = A C`. 下证 `A, C` 互素. 设 `d = (A, C)`, 则 `d | C-A = a`, `quad d | C+A = c`, 从而 `d | (a, c) = 1`, 即 `d = 1`.
因为 `A C` 是平方数, 而 `A, C` 没有公共的素因子, 所以 `A, C` 都是平方数, 可设 `C = u^2`, `quad A = v^2`. 于是 `a = u^2-v^2`, `quad c = u^2+v^2`,
`b = 2 sqrt(B^2)` `= 2 sqrt(A C)` `= 2 u v`. 最后说明 `u, v` 满足的条件. 由 `C gt A` 有 `u gt v gt 0`. 由 `(A, C) = 1` 知 `(u, v) = 1`. 由 `a = u^2 - v^2` 是奇数知 `u, v` 一奇一偶.

下面使用数形结合的直观重新证明这一定理.
1. 首先说明, 全体本原勾股数与单位圆在第一象限上的有理点一一对应. 方程两边同除以 `c^2` 得 `(a/c)^2 + (b/c)^2 = 1`, 这说明 `(a/c, b/c)` 是单位圆周上的点; 反之设 `(p, q)` 是单位圆上的有理点, 其中 `p, q` 是最简分数, 用它们分母的最小公倍数通分得到 `(p, q) = (a/c, b/c)`, 从而对应于勾股数 `(a, b, c)`. 容易说明 `(a, b, c)` 是本原的.
2. 在第一象限的单位圆周上任取一点 `P(x_P, y_P)`. 又设 `A(-1, 0)`, `k` 是 `AP` 的斜率, 则 `P` 点坐标和 `k` 的值一一对应. 显然 `P` 是有理点时, `k` 是 `(0,1)` 中的一个有理数; 下证 `k` 是 `(0,1)` 中的有理数时, 点 `P` 必为有理点. 设 `k = v/u`, 整数 `u gt v gt 0`, 我们求 `P` 的坐标, 可以用 `tan 2 alpha` 的公式; 这里用复数来处理. 由已知, `"arg"(u+"i"v) = /_ PAQ`, 将这个复数平方, 就得到一个具有两倍辐角的复数 `(u+"i"v)^2 = u^2-v^2 + 2u v"i"`. 因为同弧所对的圆心角是圆周角的两倍, 我们有 `"arg"(u+"i"v)^2 = /_ POQ`. 又 `|(u+"i"v)^2|` `= |u+"i"v|^2` `= u^2+v^2`. 利用三角形相似得到 `x_P = (u^2-v^2)/(u^2+v^2)`, `y_P = (2u v)/(u^2+v^2)`, 所以 `P` 是有理点.
3. 只要让斜率 `k` 取遍集合 `(0,1) nn QQ`, 就得到单位圆在第一象限的全部有理点, 从而得到全体本原勾股数.

可以用代数计算验证, 确实有 `(u^2-v^2)^2 + (2u v)^2 = (u^2+v^2)^2`. 由以上讨论知, 任意一个勾股三角形总是相似于边长为 `u^2-v^2, 2u v, u^2+v^2` 的三角形, 其中 `u gt v gt 0`. 代入 `(u,v) = (2,1)` 得到勾股数 `(3, 4, 5)`, 代入 `(u,v) = (3,2)` 得到勾股数 `(5,12,13)`... 试试看吧!

圆锥曲线上的有理点

[来自讲义《MIT18: Rational Points on Conics》]

将寻找勾股数的问题转化为单位圆上的有理点, 这个方法可以推广到一般的圆锥曲线. 具体来说, 齐次不定方程 `a x^2 + b x y + c y^2 + d x z + e y z + f z^2 = 0` 满足 `z != 0` 的解可以转化为寻找整系数圆锥曲线 `a x^2 + b x y + c y^2 + d x + e y + f = 0` 上的有理点. 假设 `(x_0, y_0)` 是曲线上的一个有理点, 过该点作斜率为 `k` 的直线族, 只要 `k` 取遍全体有理数 (及 `+-oo`), 直线族与曲线的交点就确定了曲线上的全体有理点. 换言之, 令 `k = p//q`, 则上述不定方程的通解可由 `p, q` 参数化, 形如 `x = x(p, q)`, `quad y = y(p, q)`, `quad z = z(p, q)`.

[来自 レイ] 证明: 单位圆上存在无数个点, 它们两两间的距离均为有理数.

[来自 折棒的网友] 记 `A(-1, 0)`, `B(1, 0)`. 对于任一组勾股数 `a^2+b^2=c^2`, 可取点 `K` 使得 `KA = 2a//c`, `KB = 2b//c`, 于是 `KA^2 + KB^2 = AB^2`, `K` 位于单位圆上. 依此法取 `K_1, K_2`, 则 `A B K_1 K_2` 是圆内接四边形, 由 Ptolemy 定理 `K_1 K_2 * AB + B K_1 * A K_2 = A K_1 * B K_2`. 因此 `K_1 K_2` 为有理数. 但勾股数有无穷多组, 所以这样的点有无穷多个.

[来自群友 我是绝妙的解析数论] 解不定方程 `1/a + 1/c = 2/b`.

[来自群友 问情明心] 方程化为 `b c + b a = 2a c`, 这是齐次方程. 和勾股数一样, 我们有两个观察: 一是只需求出本原解 `gcd(a,b,c) = 1`, 二是可以转化为曲线上的有理数解.
令 `a//b = x`, `c//b = y`, 问题化为求解曲线 `x + y = 2 x y` 上的有理点. 注意原点就是一个有理点, 取过原点的直线族 `y = k x`, `k` 是有理数. 则直线与曲线的交点是有理点; 反之曲线上的任一个有理点与原点连线的斜率是有理数. 从而只要 `k` 取遍全体有理数, 就得到曲线上的全体有理点.
令 `k = p//q` 为最简分数, 解得 `a//b = x = (1+k)/(2k)` `= (p+q)/(2p)`,
`c//b = y = (1+k)/2` `= (p+q)/(2q)`. 通分得到 `b = 2 p q`, `quad a = q(p+q)`, `quad c = p(p+q)`.

整系数圆锥曲线的化简 圆锥曲线上未必存在有理点, 一个例子是 `x^2 + y^2 = -1`. 为判定曲线 上是否存在有理点, 我们对方程 作进一步化简:
1. 配方, 将方程化为形如 `a x^2 + b y^2 + c z^2 = 0`. 这是线性代数中二次型的标准操作. 注意这里的系数 `a, b, c` 不再是原方程的 `a, b, c`, 变量 `x, y, z` 也不再是原方程的 `x, y, z`.
2. 我们可以假定系数 `a, b, c` 无平方因子. 假如 `c` 有平方因子 `d^2`, 可以换元 `d z mapsto z`, 得到新方程 `a x^2 + b y^2 + (c//d^2) z^2 = 0`, 消去这个平方因子.
3. 约去公因子后, 可以假定 `gcd(a, b, c) = 1`. 进一步可以假定 `a, b, c` 两两互素. 假如素数 `p | a`, `p | b`, 方程两边模 `p` 得到 `p | c z^2`. 但 `p !| c`, 所以 `p | z`. 因此可以换元 `z mapsto p z`, 得到新方程 `(a // p) x^2 + (b // p) y^2 + c p z^2 = 0`. 这个变换使得 `a, b` 中减少一个因子 `p`, 而 `c` 增加一个因子 `p`, 总的来说因子 `p` 是减少的.
最后我们得到方程 `a x^2 + b y^2 + c z^2 = 0`, 其中 `a b c` 无平方因子 (这等价于 `a, b, c` 各自无平方因子, 且两两互素). 是时候请出 Legendre 定理了!

Legendre 设 `a, b, c` 是非零整数, `a b c` 无平方因子, 则不定方程 `a x^2 + b y^2 + c z^2 = 0` 有非平凡解 `(x, y, z) != (0, 0, 0)` 当且仅当以下条件全部满足:
1. `a, b, c` 不同号.
2. `-a b` 是模 `c` 的二次剩余, `-b c` 是模 `a` 的二次剩余, `-a c` 是模 `b` 的二次剩余.

"`rArr`":
1. 假设不定方程有非平凡解, 则 `a, b, c` 不可能同号; 否则方程可以写为平方和的形式, 它只有平凡解.
2. 假设 `(x, y, z)` 是一组非平凡解, 不妨设 `gcd(x, y, z) = 1`, 下证 `x, y, z` 两两互素. 假如素数 `p | x`, `p | y`, 则方程两边模 `p^2` 得到 `p^2 | c z^2`. 由于 `c` 无平方因子, 所以 `p | z`, 这与 `gcd(x, y, z) = 1` 矛盾.
3. 下证 `-b c` 是模 `a` 的二次剩余. 任取 `a` 的一个素因子 `p`, 则 `b y^2 + c z^2 -= 0 (mod p)`. 由于 `y, z` 互素, `p` 不能同时整除 `y, z`. 不妨设 `p !| y`, 于是 `b y^2 -= - c z^2 (mod p)`,
   `b -= -c z^2 y^-2 (mod p)`,
   `-b c -= c^2 z^2 y^-2 (mod p)`. 因此 `-b c` 是模 `p` 的二次剩余. 由 `p` 的任意性及中国剩余定理 (CRT) 知道 `-b c` 也是模 `a` 的二次剩余.

"`lArr`":
1. 设 `-b c -= k^2 (mod a)`, 于是在模 `a` 的意义下, 可以对方程因式分解: `a x^2 + b y^2 + c z^2`
   `-= b y^2 + c z^2 (mod a)`
   `-= b(y^2 + c z^2 b^-1) (mod a)`
   `-= b(y^2 - k^2 z^2 b^-2) (mod a)`
   `-= b(y + k z b^-1) (y - k z b^-1) (mod a)`. 类似可在模 `b, c` 的意义下因式分解; 总之 `a x^2 + b y^2 + c z^2`
   `-= (alpha_1 x + beta_1 y + gamma_1 z)(rho_1 x + sigma_1 y + tau_1 z) (mod a)`
   `-= (alpha_2 x + beta_2 y + gamma_2 z)(rho_2 x + sigma_2 y + tau_2 z) (mod b)`
   `-= (alpha_3 x + beta_3 y + gamma_3 z)(rho_3 x + sigma_3 y + tau_3 z) (mod c)`. 由于 `a, b, c` 两两互素, 应用中国剩余定理 (CRT) 知道, 存在整数 `alpha` 满足 `alpha -= alpha_1 (mod a)`,
   `alpha -= alpha_2 (mod b)`,
   `alpha -= alpha_3 (mod c)`. 对其他系数也类似处理, 得到 `a x^2 + b y^2 + c z^2` `-= (alpha x + beta y + gamma z)` `(rho x + sigma y + tau z)` `quad (mod a b c)`.
2. 考虑下面区域中的整数点数目: `Omega := [0, sqrt(|b c|)) xx [0, sqrt(|c a|)) xx [0, sqrt(|a b|))`. 由于 `a, b, c` 无平方因子, `Omega` 中的整数点数目为 `prod_"cyc" (floor(sqrt(|b c|)) + 1)` `gt prod_"cyc" sqrt(|b c|)` `= |a b c|`. 由鸽巢原理, 存在不同的两点 `(x_1, y_1, z_1)`, `(x_2, y_2, z_2) in Omega` 使得 `alpha x_1 + beta y_1 + gamma z_1` `-= alpha x_2 + beta y_2 + gamma z_2` `quad (mod a b c)` 令 `(x,y,z)` `= (x_1 - x_2, y_1 - y_2, z_1 - z_2)` `!= (0,0,0)`, 则 `alpha x + beta y + gamma z -= 0` `(mod a b c)`, 从而 `a x^2 + b y^2 + c z^2 -= 0` `(mod a b c)`.
3. 一些不等式推导. 2. 中选取的 `x, y, z` 满足 `x^2 lt |b c|`, `quad y^2 lt |c a|`, `quad z^2 lt |a b|`, 由于 `a, b, c` 不同号, 不妨设 `a gt 0`, `b, c lt 0`, 则 `0 le a x^2 lt a b c`,
   `-2a b c lt b y^2 + c z^2 le 0`,
   `-2 a b c lt a x^2 + b y^2 + c z^2 lt a b c`. 但 `a x^2 + b y^2 + c z^2` 是 `a b c` 的倍数, 所以它要么等于 `0`, 要么等于 `-a b c`.
4. 假设它等于 `0`, 我们已经找到原方程的非平凡解; 若它等于 `-a b c`, 作变换 `x' = x z - b y`,
   `y' = y z + a x`,
   `z' = z^2 + a b`, 可以验证 `a {:x':}^2 + b {:y':}^2 + c {:z':}^2` `= (a b + z^2)(a b c + a x^2 + b y^2 + c z^2)` `= 0`.
5. 如果 `(x', y', z') = (0,0,0)`, 则由 `z' = 0` 推出 `z^2 = -a b`. 但 `a, b` 互素, 只能有 `a = 1`, `b = -1`. 这时方程 `x^2 - y^2 + c z^2 = 0` 显然有非平凡解 `(1, 1, 0)`.

不定方程 `2 x^2 + 3 y^2 = 4 z^2` 只有平凡解.

换元 `2z mapsto z`, 新方程 `2 x^2 + 3 y^2 - z^2 = 0` 满足 `a b c` 无平方因子, `a, b, c` 不同号, 但 `-a c = 2` 不是模 `b = 3` 的二次剩余, 因此由 Legendre 定理知道新方程只有平凡解, 从而原方程也是如此.

Fermat 大定理

不存在面积为平方数的勾股三角形.

本证明使用无穷递降法.
1. 设该勾股三角形的三边长为 `a, b, c`, 面积为 `d^2`. 若 `(a, b, c) = m gt 1`, 则 `m^2 | a b = 2 d^2`, 这推出 `m | d`. 因此不妨设 `a, b, c` 是本原的, 从而得到已知条件 `a^2 + b^2 = c^2`, `quad (a, b, c) = 1`, `quad a b // 2 = d^2`. 我们假设 `c` 是满足上述条件的最小正整数, 下面来导出矛盾.
2. 由勾股数的结论, `a, b, c` 两两互素. 设 `b` 是偶数, 则存在整数 `u, v`, 满足 `u gt v gt 0`, `quad (u, v) = 1`, `quad u, v` 一奇一偶, 使得 `a = u^2 - v^2`, `quad b = 2uv`, `quad c = u^2 + v^2`. 于是 `d^2 = a b // 2 = (u+v)(u-v) u v`.
3. 容易验证四个因子 `u+v, u-v, u, v` 两两互素. 比如 `(u+v, u-v)` `= (u+v, (u+v)+(u-v))` `= (u+v, 2 u)`, 但 `u + v` 是奇数, 因此上式等于 `(u+v, u) = (v, u) = 1`, 这推出 `(u+v, u-v) = 1`.
4. 四个互素因子的乘积是平方数 `d^2`, 由此得到这四个因子都是平方数. 设 `A = sqrt(u+v)`, `quad B = sqrt(u-v)`, `quad C = sqrt u`, `quad D = sqrt v`, `A, B, C, D` 也是两两互素的, 其中 `A gt B gt 0` 是奇数, `C, D` 一奇一偶. 注意 `2C^2 = 2u = A^2 + B^2 -= 2 (mod 4)`, 所以 `C` 是奇数, `D` 是偶数.
5. 令 `a_1 = (A+B)/2`, `quad b_1 = (A-B)/2`, `quad c_1 = C`, `quad d_1 = D/2`, 有 `a_1^2 + b_1^2 = (A^2+B^2)/2 = C^2 = c_1^2`,
   `a_1 b_1 // 2 = (A^2-B^2)/8 = v/4 = (D/2)^2 = d_1^2`. 且 `(a_1, b_1, c_1)` `= (a_1, a_1+b_1, c_1)` `= (a_1, A, C) = 1`.
6. 我们发现, `a_1, b_1, c_1` 也满足 `a, b, c` 的关系 , 但 `c_1 = C = sqrt u lt u^2+v^2 = c`, 这与 `c` 的最小性矛盾. 原命题得证.

Fermat 大定理 (Fermat's Last Theorem, FLT) 设整数 `n gt 2`, 则不定方程 `x^n + y^n = z^n` 不存在满足 `x, y, z != 0` 的整数解.

我们有以下观察:
1. 该不定方程是齐次的. 即, 若 `x, y, z` 是该方程的解, 则对任意整数 `k`, `k x, k y, k z` 也是它的解. 反之若存在非零整数 `k`, 使得 `k x, k y, k z` 是方程的解, 则 `x, y, z` 也是它的解.
2. 若 FLT 对于整数 `n` 成立, 则它对任意 `n` 的倍数也成立.
我们来证明 FLT(4), 即 `n = 4` 的情形. 设 `x^4 + y^4 = z^4`, 由观察 1, 可以假设 `(x, y, z) = 1`. 因此, `x^2, y^2, z^2` 是本原勾股数. 设 `y` 是偶数, 故存在 `u, v` 使得 `x^2 = u^2 - v^2`, `quad y^2 = 2 u v`, `quad z^2 = u^2 + v^2`. 上式表明 `u, v, z` 是勾股数, 但它们围成的直角三角形的面积 `u v // 2 = (y/2)^2` 是平方数! 矛盾.
既然 FLT(4) 已证, 由观察 2, 接下来只需考虑 `n` 为奇素数的情形. 然而, 费马大定理是非常困难的问题, 即使我有绝妙证法, 这里的空白也太小写不下.

`133^5 + 110^5 + 84^5 + 27^5 = 144^5`

平方和

二平方和

二平方和恒等式 `(x_1^2+x_2^2)(y_1^2+y_2^2) = (x_1 y_1+x_2 y_2)^2 + (x_1 y_2-x_2 y_1)^2`. 从而, 如果整数 `m, n` 能表示为两个整数的平方之和, 则 `mn` 也能.

素数 `p` 能表为两个整数的平方和当且仅当 `p = 2` 或 `p -= 1 (mod 4)`. 换言之, `4k+3` 型的素数不能表示为两个整数的平方和.

1. `p = 2` 时显然有 `2 = 1^2 + 1^2`. 注意整数 `a` 的平方模 4 余 0 或 1, 于是 `a^2 + b^2` 模 4 余 0, 1 或 2, 不可能为 3. 所以 `4k+3` 型素数不能表为平方和.
2. 下设 `p = 4k+1`. 此时 `-1` 是模 `p` 的二次剩余, 故存在 `x, m` 使得 `x^2 + 1 = m p`, 其中 `1 le x le p-1`, 于是 `m p le (p-1)^2 + 1 le (p-1)p`, 从而 `m lt p`.
3. 设 `m` 是使得关于 `x, y` 的不定方程 `x^2 + y^2 = m p` 有解的最小正整数, 由 2. 知 `m lt p`. 下证必有 `m = 1`. 首先, 若 `m` 是 `x, y` 的公因数, 则有 `m^2 | m p rArr m | p`, 再由 `m lt p` 推出 `m = 1`. 下设 `m` 不是它们的公因数, 从而 `m gt 1`, 我们来导出矛盾. 分别记 `a, b` 是 `x, y` 除以 `m` 的绝对最小余数, 则 `a, b` 不全为零, 且绝对值小于等于 `m//2`. 因此 `0 lt a^2 + b^2 le 2 (m//2)^2 = m^2//2`. 且 `a^2 + b^2 -= x^2 + y^2 -= 0` `(mod m)`, 从而 `a^2 + b^2 = m q`, `quad 0 lt q le m//2 lt m`.
4. 下证 `p q` 可以表示成两个整数的平方和, 从而推翻假设. 由二平方和恒等式 `m^2 p q = (a^2+b^2)(x^2+y^2) = (a x+b y)^2 + (a y-b x)^2`, 其中 `a x + b y -= x^2 + y^2 -= 0 (mod m)`, `quad a y - b x -= 0 (mod m)`. 这指出 `m` 是 `a x + b y` 和 `a y - b x` 的公因数, 从而 两边可以同除 `m^2`, 但 `q lt m`, 与 `m` 的最小性矛盾. 证毕.

二平方和定理 正整数 `n` 能表为两个整数的平方和当且仅当它所有的 `4k+3` 型素因子在 `n` 中的次数为偶数.

1. 充分性. 设 `n = t^2 n_1`, 其中 `n_1` 无平方因子. 若 `4k+3` 型素因子在 `n` 中的次数均为偶数, 则 `n_1` 不含 `4k+3` 型素因子, 因而 `n_1` 可以表为平方和 `a^2+b^2`, 进而 `n` 可以表为平方和 `(t a)^2 + (t b)^2`.
2. 必要性. 设 `n = x^2 + y^2`, 但存在一个素因子 `p=4k+3`, 它在 `n` 中的次数为奇数, 设这个次数为 `2j+1`. 我们可以从 `n = x^2 + y^2` 两边约去公因子 `d^2`, 而且 `p` 在 `n//d^2` 中的次数仍为奇数. 因此不妨设 `x, y` 互素. 如果 `p|x`, 则由 `p|n` 知 `p|y`, 与 `x, y` 互素矛盾. 所以 `p!|x`, `p!|y`, 此时存在整数 `z` 使得 `x z -= y` `(mod p)`. 从而有 `(1+z^2) x^2 -= x^2 + y^2 -= n -= 0` `(mod p)`, 于是 `1 + z^2 -= 0` `(mod p)`, 即 `-1` 是模 `p` 的二次剩余, 和 `p = 4k+3` 矛盾.

三平方和

三平方和定理 正整数 `n` 不能写为 3 个整数的平方和当且仅当存在非负整数 `a, b` 使得 `n = 4^a(8b+7)`.

1. `lArr`: 对 `a` 作归纳. 当 `a = 0` 时, 因为对任意整数 `x` 都有 `x^2 -= 0, 1, 4 (mod 8)`, 所以不存在三个整数 `x_1, x_2, x_3` 使得 `x_1^2 + x_2^2 + x_3^2 -= 7 (mod 8)`, 命题成立.
   假设命题对非负整数 `a` 已经成立, 即 `4^a(8b+7)` 不能写为 3 个整数的平方和, 考虑 `4^(a+1) (8b+7)`, 如果它能写为 3 个整数的平方和: `x_1^2 + x_2^2 + x_3^2 = 4^(a+1) (8b+7)`, 则 `x_i^2 !-= 1 (mod 8)`, `i = 1, 2, 3`; 因此三个数均为偶数, 从而得到 `(x_1/2)^2 + (x_2/2)^2 + (x_3/2)^2 = 4^a (8b+7)`, 与假设矛盾. 因此 `4^(a+1) (8b+7)` 不能写为 3 个整数的平方和.
2. `rArr`: 反方向的证明相当长. Gauss 给出过一个证明, 参见 [Gauss C F. Disquisitiones Arithmeticae, 1801 (《Gauss 全集》, 第一卷), 第 288-292 目]、 [Rose H E. A Course in Number Theory. Oxford University Press, 1988, 第九章定理 2.2]

四平方和

本节将证明, 任意正整数可以表为四个整数的平方和. 其证明思路与二平方和定理类似.

预备知识

Lagrange 恒等式 设 `n in ZZ^+`, `x_i, y_i in RR`, `i = 1, 2, cdots, n`, 则 `(sum_(i=1)^n x_i^2)(sum_(i=1)^n y_i^2)` `= (sum_(i=1)^n x_i y_i)^2 + sum_(1 le i lt j le n) (x_i y_j - x_j y_i)^2`. 从向量的角度理解: `|bm x|^2 |bm y|^2 = |bm x * bm y|^2 + |bm x xx bm y|^2`.

右边 `= sum_(i=1)^n x_i^2 y_i^2 + 2 sum_(1 le i lt j le n) x_i y_i x_j y_j + sum_(1 le i lt j le n) x_i^2 y_j^2` `- 2 sum_(1 le i lt j le n) x_i y_j x_j y_i + sum_(1 le i lt j le n) x_j^2 y_i^2` `= sum_(i=1)^n x_i^2 y_i^2 + sum_(1 le i lt j le n) x_i^2 y_j^2 + sum_(1 le i lt j le n) x_j^2 y_i^2 =`左边.

四平方和恒等式 (Euler, 1743) `(sum_(i=1)^4 x_i^2)(sum_(i=1)^4 y_i^2) = sum_(i=1)^4 z_i^2`. 其中 `z_1 = x_1 y_1 + x_2 y_2 + x_3 y_3 + x_4 y_4`,
`z_2 = x_1 y_2 - x_2 y_1 + x_3 y_4 - x_4 y_3`,
`z_3 = x_1 y_3 - x_3 y_1 + x_4 y_2 - x_2 y_4`,
`z_4 = x_1 y_4 - x_4 y_1 + x_2 y_3 - x_3 y_2`. 从而, 如果整数 `m, n` 能表示为四个整数的平方之和, 则 `mn` 也能.

由 Lagrange 恒等式, 只需验证 `(x_1 y_2 - x_2 y_1)(x_3 y_4 - x_4 y_3)` `- (x_1 y_3 - x_3 y_1)(x_2 y_4 - x_4 y_2)` `+ (x_1 y_4 - x_4 y_2)(x_2 y_3 - x_3 y_2) = 0`. 即可. 上式的左边可由 Laplace 定理展开行列式 `|x_1,x_2,x_3,x_4; y_1,y_2,y_3,y_4; x_1,x_2,x_3,x_4; y_1,y_2,y_3,y_4|` 得到.

如果令 `bm x, bm y, bm z` 表示四元数 `bm x = x_1 - x_2 bb i + x_3 bb j - x_4 bb k`,
`bm y = y_1 + y_2 bb i - y_3 bb j + y_4 bb k`,
`bm z = z_1 + z_2 bb i - z_3 bb j + z_4 bb k`, 则 `bm x bm y = x_1 y_1 + x_2 y_2 + x_3 y_3 + x_4 y_4` `+ (x_1 y_2 - x_2 y_1 + x_3 y_4 - x_4 y_3) bm i` `- (x_1 y_3 - x_3 y_1 + x_4 y_2 - x_2 y_4) bm j` `+ (x_1 y_4 - x_4 y_1 + x_2 y_3 - x_3 y_2) bm k` `= bm z`. 因此四平方和恒等式可以简记为 `|bm x| |bm y| = |bm x bm y|`.

(Euler, 1751) 对任意奇素数 `p`, 同余方程 `x^2+y^2+1 = 0` `(mod p)` 存在整数解 `0 le x, y lt p//2`. 因此对任意奇素数 `p`, 存在正整数 `m` 和整数 `0 le x, y le (p-1)//2`, 使得 `m p = x^2 + y^2 + 1 le (p-1)^2//2 + 1` `lt (p-1)(p+1) + 1 = p^2`. 因此 `m lt p`.

模 `p` 的二次剩余 (即全体平方数 `ZZ^2` 模 `p` 的同余类) 有 `(p+1)//2` 个, 分别为 `0, 1^2, 2^2, cdots, ((p-1)/2)^2`. 若 `(p-1)//2` 是模 `p` 的二次剩余, 则存在 `0 le x lt p//2` 使得 `x^2 -= (p-1)//2` `(mod p)`, 于是 `1 + x^2 + x^2 -= 0` `(mod p)`, 定理得证.
若 `(p-1)//2` 不属于模 `p` 的二次剩余, 将模 `p` 的剩余 (即全体整数模 `p` 的同余类) 分为如下 `(p-1)//2` 组: `{0, p-1}, {1, p-2}, cdots, {(p-1)/2, (p-1)/2}`. 而模 `p` 的 `(p+1)//2` 个二次剩余必然落在前 `(p-3)//2` 组当中. 由鸽巢原理, 必有两个二次剩余落在同一组中. 由于每一组的两个元素 `m, n` 满足 `m + n + 1 -= 0` `(mod p)`, 故存在整数 `x, y`, `0 le x, y lt p/2`, 使 `x^2 + y^2 + 1 -= 0` `(mod p)`.

四平方和定理

四平方和定理 (Lagrange, 1770; Euler, 1773) 任何非负整数都可以表示为四个整数的平方之和, 即不定方程 `x_1^2 + x_2^2 + x_3^2 + x_4^2 = n`, `quad n ge 0` 恒有整数解.

1. 显然定理对 `n = 0, 1, 2` 成立: `0 = 0^2 + 0^2 + 0^2 + 0^2`,
   `1 = 0^2 + 0^2 + 0^2 + 1^2`,
   `2 = 0^2 + 0^2 + 1^2 + 1^2`. 从而由四平方和恒等式知, 只需证定理对任意奇素数 `p` 成立. 又由, 存在最小的正整数 `m lt p` 使得 `m p` 能表示为四个整数的平方和: `m p = x_1^2 + x_2^2 + x_3^2 + x_4^2`.
2. 下证 `m` 不是偶数, 否则 `m p` 为偶数, `x_i, i = 1, 2, 3, 4` 中的奇数只能是偶数个 (即 0, 2, 4 个). 不失一般性, 设 `x_1, x_2` 奇偶性相同, 且 `x_3, x_4` 奇偶性相同, 则 `x_1+-x_2`, `x_3+-x_4` 均为偶数, 得到 `(m//2)p = ((x_1+x_2)/2)^2 + ((x_1-x_2)/2)^2` `+ ((x_3+x_4)/2)^2 + ((x_3-x_4)/2)^2`. 然而 `m//2 lt m`, 这与 `m` 的最小性矛盾.
3. 下证 `m = 1`. 首先, 若 `m` 为 `x_1, x_2, x_3, x_4` 的公因数, 则有 `m^2 | m p` `rArr m | p`, 再由 `m lt p` 推出 `m = 1`. 下设 `m` 不是它们的公因数, 从而 `m` 是大于 `1` 的奇数, 我们来导出矛盾. 取 `y_i` 为 `x_i` 除以 `m` 的绝对最小余数, `i = 1, 2, 3, 4`: `y_i -= x_i` `(mod m)`, `quad i = 1, 2, 3, 4`. 则 `y_i` 不全为零, 且绝对值小于 `m//2` (注意 `m` 是奇数). 因此 `0 lt sum_(i=1)^4 y_i^2 lt 4(m/2)^2 = m^2`, 且 `sum_(i=1)^4 y_i^2 -= sum_(i=1)^4 x_i^2 -= 0` `(mod m)`, 从而 `sum_(i=1)^4 y_i^2 = m q`, `quad 0 lt q lt m`.
4. 下证 `p q` 可以表示成四个整数的平方和, 从而推翻假设. 由四平方和恒等式, 令 `sum_(i=1)^4 z_i^2 = (sum_(i=1)^4 x_i^2) (sum_(i=1)^4 y_i^2) = m^2 p q`, 其中 `z_1 = x_1 y_1 + x_2 y_2 + x_3 y_3 + x_4 y_4`,
   `z_2 = x_1 y_2 - x_2 y_1 + x_3 y_4 - x_4 y_3`,
   `z_3 = x_1 y_3 - x_3 y_1 + x_4 y_2 - x_2 y_4`,
   `z_4 = x_1 y_4 - x_4 y_1 + x_2 y_3 - x_3 x_2`. 由 `x_i -= y_i (mod m)`, `i = 1, 2, 3, 4`, 有 `z_1 -= sum_(i=1)^4 x_i^2 -= 0` `(mod m)`,
   `z_i -= 0 (mod m)`, `i = 2, 3, 4`. 这指出 `m` 是 `z_1, z_2, z_3, z_4` 的公因数, 从而 `p q = sum_(i=1)^4 (z_i//m)^2`. 但 `q lt m`, 与 `m` 的最小性矛盾. 证毕.

[来自 Brilliant] 基于三平方和定理, 可以较简单地证明四平方和定理. 事实上我们只需考虑那些不能写为三平方和的数: `n = 4^a(8b+7)`, `a, b` 为非负整数. 此时 `n` 模 4 余 0 或 3.
1. 若 `n -= 0 (mod 4)`, 则只要 `n//4` 可以写为四平方和: `x^2 + y^2 + z^2 + w^2 = n//4`, 就有 `(2x)^2 + (2y)^2 + (2z)^2 + (2w)^2 = n`. 因此我们只需考虑 `n !-= 0 (mod 4)` 的情况.
2. 若 `n -= 3 (mod 4)`, 则 `n-1` 可以写为三平方和, 再加上 1 就得到四平方和.

推广: n 角数

n 角数 (多边形数) [来自 tamagaki 的博客] 考虑一组共用两条边的正 `n` 边形, 其中第 `k` 个正 `n` 边形每条边有 `k` 个点, 用 `P(n, k)` 表示这个图形中的点数, 称为 `n` 角数 (`n ge 3`, `k ge 1`).

• 递推公式: `P(n, 1) = 1`, `P(n, k) = P(n, k-1) + (n-2)(k-1)+1`;
• 通项公式: `P(n, k)` `= 1 + (n-2) sum_(j=2)^k (j-1) + (k-1)` `= (n-2)k(k-1)//2 + k`;

费马多边形数定理 (Fermat polygonal number theorem)
任意正整数都可以写为不超过 `n` 个 `n` 角数之和 (`n ge 3`). 考虑以下两个特例:
1. `n = 4` 时, 即为四平方和定理 (Lagrange, 1770).
2. `n = 3` 时, 即: 任意正整数都能写成不超过三个三角形数之和 (Gauss, 1796).
一般的情况由 Cauchy 在 1813 年证明.

[来自 Brilliant] 我们给出 Gauss 对于 `n = 3` 情形的证明. 对任意正整数 `a`, 由三平方和定理知道, `8a+3` 可以写成 3 个整数的平方和: `x_1^2 + x_2^2 + x_3^2 = 8a+3`. 由于对任意整数 `x`, `x^2` 模 8 的余数只能是 0, 1 或 4, 所以由上式知道 `x_i -= 1 (mod 8)`, `i = 1, 2 , 3`, 即 `x_1, x_2, x_3` 都是奇数. 令 `x_1 = 2x+1`, `x_2 = 2y+1`, `x_3 = 2z+1`, 有: `(2x+1)^2 + (2y+1)^2 + (2z+1)^2 = 8a+3`, 变形得到 `(x(x+1))/2 + (y(y+1))/2 + (z(z+1))/2 = a`.

Pell 方程

设 `d` 为正整数, 且不是平方数, 下面的不定方程称为 Pell 方程: `x^2 - d y^2 = 1`.

Pell 方程的幂形式解 将 Pell 方程的全部正整数解 `x_k, y_k` (后面会证明 Pell 方程确实有解) 按 `lambda_k = x_k + sqrt d y_k` 的值由小到大排列, 有 `lambda_k = lambda_1^k`, `quad k = 1, 2, cdots`. 因此, 由 Pell 方程的最小正整数解 `x_1, y_1` 可以轻松得到通解.

取共轭 `lambda_k' = x_k - sqrt d y_k`, 由 `x_k, y_k` 满足 Pell 方程知道 `lambda_k lambda_k' = 1`. 下面证明, Pell 方程的正整数解 `x, y` 均满足 `x + sqrt d y = lambda_1^k`, 其中 `k` 为某个正整数.
1. 记 `x + sqrt d y = lambda_1^k`, 由于 `(x + sqrt d y)(x - sqrt d y)` `= lambda_1^k (lambda_1^k)'` `= lambda_1^k (lambda_1')^k` `= (lambda_1 lambda_1')^k = 1`, 所以 `x, y` 是一组正整数解.
2. 反之令 `x, y` 是一组正整数解, 且 `lambda = x + sqrt d y` 不等于任何一个 `lambda_1^k`. 因为 `lim_(k to oo) lambda_1^k = oo`, 可以设 `lambda_1^k lt lambda lt lambda_1^(k+1)` 同乘以 `lambda_1^-k = (lambda_1')^k` 得 `1 lt s + sqrt d t lt lambda_1`, 其中 `s + sqrt d t = lambda (lambda_1')^k`. 注意到 `0 lt s - sqrt d t lt 1 lt s + sqrt d t`, 有 `s = 1/2((s + sqrt d t) + (s-sqrt d t)) gt 0`,
   `t = 1/(2 sqrt d) ((s + sqrt d t) - (s - sqrt d t)) gt 0`, 且 `(s + sqrt d t)(s - sqrt d t)` `= lambda (lambda_1')^k lambda' lambda_1^k = 1`, 说明 `s, t` 也是一组正整数解, 然而 `s + sqrt d t lt lambda_1`, 与 `lambda_1` 的最小性矛盾.

设 `d in ZZ^+` 不是平方数, 若不定方程 `x^2 - d y^2 = n` 有最小正整数解 `x_0, y_0`, 则通解 `mu = x + sqrt d y` 由下式给出: `mu_k = mu_0 lambda_1^k`, `quad k = 0, 1, 2, cdots`. 其中 `lambda_1` 对应 Pell 方程 `x^2 - d y^2 = 1` 的最小正整数解.

1. 首先验证 `mu_k = x_k + sqrt d y_k` 确实给出方程的解. 我们有 `(x_k + sqrt d y_k)(x_k - sqrt d y_k)` `= mu_k mu_k'` `= mu_0 mu_0' lambda_1^k (lambda_1')^k` `= mu_0 mu_0'` `= n`.
2. 反之令 `x, y` 是一组正整数解, 且 `mu = x + sqrt d y`, 类似可证 ??

1. 稍加尝试可以知道, 不定方程 `x^2 - 2 y^2 = 1` 的最小正整数解为 `(3, 2)` (依次尝试 `y = 1, 2, 3...`, 看 `1 + 2y^2` 何时为平方数). 记 `lambda = 3 + 2 sqrt 2`, 则 `lambda^2 = 17+12√2`, `lambda^3 = 99+70√2`, `lambda^4 = 577+408√2`, `cdots` 对应于正整数解 `(17, 12)`, `(99, 70)`, `(577, 408)`, `cdots`.
2. 不定方程 `x^2 - 2 y^2 = 2` 的最小正整数解为 `(2, 1)`. 这个方程的通解由下式生成: `(2+√2)(3+2√2)^n`, `quad n = 0, 1, 2, cdots` 即 `2+√2`, `10+7√2`, `58+41√2`, `338+239√2`, `1970+1393√2`, `cdots` 其中 `(3, 2)` 是 1. 中方程的最小正整数解.

化简 `root 3 (20+14sqrt2)`.

记 `lambda = x + y sqrt2`, 其共轭 `lambda' = x - y sqrt2`. 如果 `lambda^3 = 20+14 sqrt2`, 则有 `(x^2 - 2 y^2)^3` `= (lambda lambda')^3` `= lambda^3 (lambda^3)'` `= (20 + 14 sqrt2)(20-14 sqrt2) = 2^3`. 解不定方程 `x^2 - 2 y^2 = 2`, 得到最小正整数解 `x = 2`, `y = 1`, 发现恰有 `root 3 (20+14sqrt2) = 2 + sqrt 2`.

若 `d` 是正整数且不是平方数, 不定方程 `x^2 - d y^2 = n^k` 有正整数解 `x_k, y_k`, 问 `x^2 - d y^2 = n` 是否有正整数解 `x_1, y_1`, 使得 `(x_1 + sqrt d y_1)^k = x_k + sqrt d y_k` ?

我们来说明 Pell 方程确实有解.

三角数中有无穷多个平方数, 换言之方程 `x^2 = y(y+1)//2` 有无穷多整数解.

`y` 与 `y+1` 互素, 而乘积是平方数的两倍, 因此它们一个是平方数 `u^2`, 另一个是平方数的两倍 `2v^2`, 其中 `u v = x`. 当 `y` 是偶数时, `y = 2v^2`, `y+1 = u^2`, 对应 Pell 方程 `u^2 - 2v^2 = 1`, 它有无穷多整数解. 当 `y` 是奇数时, 同理对应 Pell 方程 `u^2 - 2 v^2 = -1` 的解.

椭圆曲线

[来自 Elliptic Curve Cryptography: a gentle introduction, 加藤和也等《数论I: Fermat 的梦想和类域论》]

域 `K` (特征 `ne 2`) 上的椭圆曲线是指方程 `y^2 = x^3 + a x + b`, `quad a, b in K`, 且等号右边的 `x^3 + a x + b` 无重根.

1. 椭圆曲线并非真的椭圆, 而是在计算椭圆周长时涉及到的对象.
2. 可以用判别式 `Delta = -(4a^3 + 27b^2)` 是否为零来判断方程右边有无重根. 如果有重根, 则曲线有尖点或与自身相交, 这种曲线不称为椭圆曲线.

椭圆曲线上的有理点群 我们考察直线 `y = k x + c` 与椭圆曲线 `y^2 = x^3+a x + b` 的位置关系. 联立方程知道, 直线与椭圆曲线有 1 个或 3 个交点 (切点视作两个重合的交点). 特别关注 3 个交点的情况. 此时由 Vieta 定理有 `x_1 + x_2 + x_3 = k^2`. 已知前两个交点 `P_1, P_2` 时, 第三个交点 `P_3` 的坐标为 `x_3 = k^2 - x_1 - x_2`,
`y_3 = y_1 + k(x_3-x_1)` `= y_2 + k(x_3-x_2)`. `P_1, P_2` 都是椭圆曲线上的有理点时, `P_3` 也是有理点. 我们对椭圆曲线上的全体有理点 (补充一个无穷远点) 规定加法运算, 使它构成 Abel 群:
1. 加法零元是竖直方向上的无穷远点, 记为 0; 注意它不是坐标原点.
2. 加法逆元关于 `x` 轴对称.
3. 若椭圆曲线上 `P_1, P_2, P_3` 三点共线, 则 `P_1 + P_2 + P_3 = 0`. 换言之, `P_1 + P_2 = -P_3`, 因此 `P_1 + P_2` 是 `P_3` 关于 `x` 轴的对称点.
4. 上述关系对于切点或无穷远点的情形仍成立: 若 `P` 是切点, `Q` 是第三个交点, 则有 `2P + Q = 0`; 若 `P, Q` 关于 `x` 轴对称, 则它们可以看作与竖直方向的无穷远点共线, 故 `P + Q = 0`. 特别当 `P` 是曲线与 `x` 轴的交点时, `2P = 0`.

一般而言, 椭圆曲线上的整点只有有限个 (Siegel 定理), 但有理点可能为无限个, 也可能为有限个.

考虑椭圆曲线 `y^2 = x^3 - x = x(x+1)(x-1)`, 它有 3 个明显的有理点 `P_0(0, 0)`, `P_1(1, 0)`, `P_2(-1, 0)`. 假设 `Q(x, y)` 也是曲线上的有理点, 求 `P_0 + Q`, `P_1 + Q` 和 `2Q`.

1. `P_0(0, 0) + Q(x, y)`: `k = y/x`, `quad k^2 = y^2/x^2 = ((x+1)(x-1))/x`,
   `x' = k^2 - 0 - x = 1/x(x^2-1-x^2) = -1/x`,
   `-y' = 0 + k(x' - 0) = -y/x^2`. 因此 `P_0 + Q = (-1/x, y/x^2)`.
2. `P_1(1, 0) + Q(x, y)`: `k = y/(x-1)`, `quad k^2 = y^2/(x-1)^2 = (x(x+1))/(x-1)`,
   `x' = k^2 - 1 - x = 1/(x-1)(x(x+1) - (x+1)(x-1)) = (x+1)/(x-1)`,
   `-y' = 0 + k(x' - 1) = (2y)/(x-1)^2`. 因此 `P_1 + Q = ((x+1)/(x-1), -(2y)/(x-1)^2)`.
3. `2Q(x, y)`: 曲线两边对 `x` 求导得 `2y k = 3x^2-1`. 从而 `k = (3x^2-1)/(2y)`, `quad k^2 = (3x^2-1)^2/(4x(x+1)(x-1))`,
   `x' = k^2 - 2x = (x^2+1)^2/(4y^2)`,
   `-y' = y + k(x'-x) = (((x-1)^2-2)(x^2+1)((x+1)^2-2))/(8y^3)`.

---

# 椭圆曲线群的加法
def add(x0, y0, x1, y1, y, expr):
    k = (y1-y0)/(x1-x0) if x1 != x0 else diff(expr**2)/(2*y)
    x_res = expand(k**2-x0-x1).replace(y, expr).simplify()
    y_res = expand(-y0-k*(x_res-x0)).replace(y, expr).simplify()
    return x_res, y_res

add(0, 0, x, y, y, sqrt(x**3-x)) # (-1/x, sqrt(x**3 - x)/x**2)
add(1, 0, x, y, y, sqrt(x**3-x)) # ((x + 1)/(x - 1), -2*sqrt(x**3 - x)/(x**2 - 2*x + 1))
add(x, y, x, y, y, sqrt(x**3-x)) # ((x**4 + 2*x**2 + 1)/(4*x*(x**2 - 1)), (x**6 - 5*x**4 - 5*x**2 + 1)/(8*x*sqrt(x*(x**2 - 1))*(x**2 - 1)))

勾股三角形与椭圆曲线 设 `d` 为正有理数, 以下三个命题等价:
1. 存在面积为 `d`, 三边长为有理数的直角三角形.
2. 存在三个有理数的平方, 构成公差为 `d` 的等差数列.
3. 椭圆曲线 `y^2 = x^3 - d^2 x` `= x(x+d)(x-d)` 上存在非平凡的有理点 `(x, y)`, 其中 `y != 0`.
这个命题可以推广到特征不为 2 的域.

1. `iff` 2: 设 `a, b, c` 是正有理数, `a^2+b^2=c^2`, `a b//2 = d`, 令 `u = (b-a)//2`, `v = c//2`, `w = (a+b)//2`, 则 `u^2 = (a-b)^2//4`, `quad v^2 = (a^2+b^2)//4`, `quad w^2 = (a+b)^2//4` 构成公差为 `d` 的等差数列. 反之由 `(u, v, w)` 出发构造逆映射也能得到 `(a, b, c)`: `a = w-u`, `quad b = w+u`, `quad c = 2v`.
2. `iff` 3: 设 `u^2, v^2, w^2` 构成公差为 `d` 的等差数列, 令 `x = v^2`, `y = u v w`, 则 `y^2 = (u v w)^2` `= v^2(v^2+d)(v^2-d)` `= x(x+d)(x-d)`. 然而这个映射的逆不是有理函数, 也不能保证 `y != 0`. 好在我们还有另一个较复杂的映射 `x = (u+v)(v+w)`, `quad y = (u+v)(v+w)(w+u)`, 其具有逆映射 `u = 1/(2y) ((x-d)^2 - 2d^2)`, `quad v = 1/(2y) (x^2 + d^2)`, `quad w = 1/(2y) ((x+d)^2 - 2d^2)`. 这里 `y != 0`, 否则它必有一个因子为零, 这使得 `u^2, v^2, w^2` 全相等, 与 `d gt 0` 矛盾. 用 sympy 验证 `(x, y)` 适合椭圆曲线 `y^2 = x(x+d)(x-d)`:

   z = u*v+v*w+w*u
   y = (u+v)*(v+w)*(w+u)
   expand((u**2+z)*(v**2+z)*(w**2+z)-y**2) # 0
   

   验证逆映射:

   u = ((x-d)**2-2*d**2)/(2*y)
   v = (x**2+d**2)/(2*y)
   w = ((x+d)**2-2*d**2)/(2*y)
   simp = lambda e: expand(e).replace(d, sqrt((x**3-y**2)/x)).simplify()
   simp((u+v)*(v+w)) # x
   simp((u+v)*(v+w)*(w+u)) # y
   

   验证等差数列:

   simp(v**2-u**2-d) # 0
   simp(v**2-w**2+d) # 0
   

证明过程中用到的映射 `g(x, y) = 1/(2y)((x-d)^2 - 2d^2, x^2+d^2, (x+d)^2 - 2d^2)`,
`h(u, v, w) = (v^2, u v w)`, 它们的复合 `h@g` 恰好是椭圆曲线上的 2 倍映射, 即 `P mapsto 2P`: `h@g(x, y) = ((x^2+d^2)^2/(4y^2), (((x-d)^2-2d^2)(x^2+d^2)((x+d)^2-2d^2))/(8y^3))`.

直角三角形 `(a, b, c) = (3, 4, 5)` 的面积为 `d = 6`, 对应椭圆曲线 `y^2 = x^3 - d^2 x = x^3 - 36x` 的有理点 `(18, 72)`. 通过 2 倍映射, 可以再构造一个面积为 6 的直角三角形: `((2a b c)/(b^2-a^2), (b^2-a^2)/(2c), (c^4+4a^2 b^2)/(2c(b^2-a^2)))` `= (120/7, 7/10, 1201/70)`.

# 推导构造直角三角形的公式
d = a*b/2
u, v, w = (b-a)/2, c/2, (a+b)/2
x, y = v**2, u*v*w
uu = ((x-d)**2 - 2*d**2)/(2*y)
vv = (x**2+d**2)/(2*y)
ww = ((x+d)**2 - 2*d**2)/(2*y)
aa, bb, cc = ww-uu, ww+uu, vv*2
simplify(aa) # -2*a*b*c/(a**2 - b**2)
simplify(bb).replace(c, sqrt(a**2+b**2)).simplify() # (-a**2 + b**2)/(2*sqrt(a**2 + b**2))
simplify(cc) # (-4*a**2*b**2 - c**4)/(2*c*(a - b)*(a + b))

[来自 知乎专栏] 求这个不定方程的正整数解: `(🍎)/(🍌+🍍) + (🍌)/(🍍+🍎) + (🍍)/(🍎+🍌) = 4`,
`(a)/(b+c) + (b)/(c+a) + (c)/(a+b) = 4`.

from fractions import Fraction
from math import lcm

def add(x0, y0, x1, y1, args):
    if y0 is None:
        return x1, y1
    if y1 is None:
        return x0, y0
    if x0 == x1 and y0 != y1:
        return None, None
    k = Fraction(y1-y0, x1-x0) if x1 != x0 else Fraction(3*x0**2 + 2*args[2]*x0 + args[1], 2*y0)
    x_res = k**2-args[2]-x0-x1
    y_res = -y0-k*(x_res-x0)
    return x_res, y_res

p = (-100, 260)
q = (-100, 260)
a, b, c = (4, -1, 11)
args = (0, 224, 109)
n = 1
while not ((a < 0 and b < 0 and c < 0) or (a > 0 and b > 0 and c > 0)):
    n += 1
    q = add(*p, *q, args)
    x, y = q
    print(f'{n}P = ({x}, {y})')
    a, b, c = Fraction(56-x+y, 56-14*x), Fraction(56-x-y, 56-14*x), Fraction(-28-6*x, 28-7*x)

d = lcm(a.denominator, b.denominator, c.denominator)
print(f'a = {a * d}\nb = {b * d}\nc = {c * d}')

2P = (8836/25, -950716/125)
3P = (-731025/11881, 527529870/1295029)
4P = (561561391876/8356702225, -687837762272090924/763927933898375)
5P = (-425869857827702500/15192076294211881, 448412887098983162164732300/1872516697802137088411221)
6P = (252785840525963937198721/13225347684085115955600, -343764653760831645784970282294394569/1520934975898868459000385442296000)
7P = (-1872773018543093075805479817148900/163350615997049698719631653803161, 211390151297491981533823798000243842339853402161620/2087762847145230771938050768331341412318712353341)
8P = (8304830821343520148948729081523501917420036/1462178082526064533227321540886890051021025, -124668752376211382766812793520103329799089543359986485854396841484/1768073864797815348625142542347514156118825216532230801892732625)
9P = (-66202368404229585264842409883878874707453676645038225/13514400292716288512070907945002943352692578000406921, 58800835157308083307376751727347181330085672850296730351871748713307988700611210/1571068668597978434556364707291896268838086945430031322196754390420280407346469)
a = 154476802108746166441951315019919837485664325669565431700026634898253202035277999
b = 36875131794129999827197811565225474825492979968971970996283137471637224634055579
c = 4373612677928697257861252602371390152816537558161613618621437993378423467772036

Mordell 定理 `QQ` 上的椭圆曲线群 `E(QQ)` 是有限生成 Abel 群: 存在 `P_1, cdots, P_r in E(QQ)`, 使得任意 `P in E(QQ)` 都能表示为 `P_1, cdots, P_r` 的线性组合: `P = sum k_i P_i`. 这个群的秩称为该椭圆曲线的秩. 又根据 Mazur[1977] 的结果, `E(QQ)` 的挠子群 (有限阶元素组成的子群) 在同构意义下只有以下几种: `ZZ//n ZZ`, `quad 1 le n le 10 or n = 12`.
`ZZ/n ZZ o+ Z//2 ZZ`, `quad n = 2, 4, 6, 8`.

椭圆曲线上的离散对数问题 设 `p` 为奇素数, 考虑有限域 `bbb F_p` 中的椭圆曲线, 它的加法群定义与 `QQ` 上的完全相同, 只不过运算是模 `p` 的. 一个计算困难的问题是: 已知两点 `P, Q`, 求 `k` 使得 `Q = k P`. 这称为椭圆曲线上的离散对数问题, 也是许多加密算法的基础.

Schoof 算法 可在多项式时间内求椭圆曲线群 `G` 的阶. 知道了群 `G` 的阶后, 元素 `P` 的阶就是 `G` 的因子中使得 `k P = 0` 成立的最小 `k`.
给定素数 `q`, 可按如下方法在 `G` 中找一个 `q` 阶元: 计算 `|G| // q = h`, 然后任取 `P in G`, 则 `q(h P) = |G| P = 0`, 这指出 `h P` 的阶是 `q` 的因子, 但 `q` 为素数, 所以 `h P = 0` 或 `|h P| = q`.

杂例

解关于 `x, y` 的不定方程 `a x y+b x+c y+d = 0`, `a, b, c, d` 为整数.

两边同乘 `a` 以后变形为 `(a x+c)(a y+b) = b c-a d`, 再讨论 `b c-a d` 的因子即可.

解关于 `a, b, c, d` 的不定方程 `1/a + 1/b + 1/c + 1/d = 1`, `a, b, c, d` 是两两不相等的正整数.

解关于 `x, y` 的不定方程 `x^2 + 615 = 2^y`.

1. 模 2: 显然 `y` 只能是正整数, 于是 `2^y` 是偶数. 这推出方程左边是偶数, 于是 `x` 是奇数.
2. 模 3: `2^y` 不是 3 的倍数, 但 615 是 3 的倍数, 于是 `x` 不是 3 的倍数.
3. 模 6: 综上可知 `x = 6n+-1`, 于是 `x^2 -= 1 (mod 6)`. 而 `615 -= 3 (mod 6)`, 得到 `2^y -= 4(mod 6)`. 这推出 `y` 是偶数.
4. 设 `y = 2n`, 原方程变形为 `(2^n - x)(2^n + x) = 615 = 3*5*41`, 我们只需寻找 `(a, b)` 满足 `a + b = 2^(n+1)`, 其中 `a, b in {3, 5, 41}`. 容易发现只有两组解 `(a, b) = (5, 123)` 或 `(123, 5)`. 于是 `2^n +- x = 5`, `quad 2^n ± x = 123`. 解得 `n = 6`, (于是 `y = 12`), `x = +-59`.

[来自 我是小学二年级的屑] 求 `{ x y = 4 n; x+y = n+2 :}` 的正整数解.

[来自 CBY 博士] 由已知 `x, y = (n+2+-sqrt((n-6)^2-32))/2`. 令判别式 `(n-6)^2-32 ge 0` 得 `n ge 12`. 令 `m = n-6 ge 6`, 则 `x = 4 + (m-sqrt(m^2-32))/2` `= 4 + 16/(m+sqrt(m^2-32))`. 因此 `4 lt x` `le 4 + 16/(6+sqrt(6^2-32)) = 6`, 即 `x = 5, 6`.
1. `x = 6` 对应 `m = 6`, `n = 12`, 这时 `y = 8`.
2. `x = 5` 对应 `m - sqrt(m^2 - 32) = 2`, 即 `m = 9`, `n = 15`, 这时 `y = 12`.

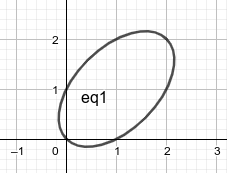
求 `(x+y)^2 = x^3 + y^3` 的正整数解.

两边同时约去正因子 `x+y` 得 `x+y = x^2 - x y + y^2`, 这是椭圆的方程, 由图像我们推测正整数解只有 `(1,2)`, `(2,1)`, `(2,2)`. [来自 我是费马方程的正整数解] 上式视为 `x` 的方程, 令它的判别式 `ge 0`, 我们得到 `y = 1, 2`, 从而轻松得到结果.

求 `x^3 + y^3 = z^2` 的正整数解.

令 `(x, y, z) = (a c, b c, c^2)`, 问题化为 `a^3 c^3 + b^3 c^3 = c^4`, 显然 `c != 0`, 得 `a^3 + b^3 = c`. 任取 `a, b in ZZ^+`, `(x, y, z) = (a (a^3+b^3), b (a^3+b^3), (a^3+b^3)^2)` 都给出原方程的一组正整数解; 如 `a=1, b=1` 时得到 `(2, 2, 4)`, `a=1, b=2` 时得到 `(9, 18, 81)` 等. 其它形式的解??

[来自 马上开学的菜狗] 求 `x^3 + y^3 = x^2 y^2` 的正整数解.

[来自 小猿搜题] 取参数 `t = x // y`, 方程化为 `(t^3+1) y^3 = t^2 y^4`, 从而 `{ x = t^2 + 1//t; y = t + 1//t^2 :}` `t = 1` 时, 得到一组解 `x = y = 2`. `t gt 1` 时, ??

[来自 叉叉子] 证明不定方程 `2x^4 = y^4 - 17 z^4` 只有平凡解 `x = y = z = 0`.

由于方程齐次, 不妨令 `gcd(x, y, z) = 1`, 考虑 mod 17 的可能余数: `{: 2x^4, y^4, 17z^4; 0, 0, 0; +-2, +-1, ; +-8, +-4, ; :}` 等式不能成立, 一个矛盾.

[来自 IMO1988 | 出题人 Stephan Beck] 设非负整数 `a, b` 使得 `(a^2+b^2)/(1+a b)` 为整数. 求证: 这个整数必是某一整数的平方.

关于平方和的立方和的几个恒等式 [来自群友 太阳花]
1. 共 8 项: `x^2 + (x+3)^2 + (x+5)^2 + (x+6)^2` `= (x+1)^2 + (x+2)^2 + (x+4)^2 + (x+7)^2`;
2. 共 12 项: `x^2 + (x+2)^2 + (x+6)^2` `+ (x+7)^2 + (x+8)^2 + (x+10)^2` `= (x+1)^2 + (x+3)^2 + (x+4)^2` `+ (x+5)^2 + (x+9)^2 + (x+11)^2`.
3. 共 16 项: expand(x**3 + (x+3)**3 + (x+5)**3 + (x+6)**3 + (x+9)**3 + (x+10)**3 + (x+12)**3 + (x+15)**3 - (x+1)**3 - (x+2)**3 - (x+4)**3 - (x+7)**3 - (x+8)**3 - (x+11)**3 - (x+13)**3 - (x+14)**3)