有序组

(Kuratowski) 对任意 `x, y`, 定义 `(x, y) := {{x},{x,y}}`, 称为由 `x, y` 组成的有序对 (ordered pair, 或有序二元组). 这个集合的存在惟一性分别由配对公理和外延公理保证.

`(x, y) = (u, v) iff x = u and y = v`.

`(x,y) = (u,v)` `iff {{x},{x,y}} = {{u},{u,v}}` `iff ({x} = {u} and {x,y} = {u,v})` `or ({x} = {u,v} and {x,y} = {u})` `iff (x = u and y = v) or (x = y = u = v)` `iff x = u and y = v`.

1. `x, y in S rArr (x, y) in 2^(2^S)`;
2. `(x,y) in S rArr x, y in uuu(uuu S)`.

1. 由 `x,y in S` 得 `{x}, {x,y} in 2^S`, 从而 `(x,y) = {{x},{x,y}} in 2^(2^S)`.
2. 由 `{{x},{x,y}} in S` 得 `{x}, {x,y} in uuu S`, 从而 `x, y in uuu(uuu S)`.

注意, 不能用类似 Kuratowski 定义有序对的方式来定义有序三元组: 假设 `(x,y,z) := {{x},{x,y},{x,y,z}}`, 则 `(a,a,b) = {{a},{a},{a,b}}` `= {{a},{a,b}}` `= {{a},{a,b},{a,b}} = (a,b,a)`. 这不是我们想要的性质.

对任意 `x_1, x_2, cdots, x_n` 递归地定义 `(x_1, x_2, cdots, x_n) := ((x_1, cdots, x_(n-1)), x_n)`, 称为有序 `bm n` 元组.

Descartes 积

对任意集合 `A, B`, 存在集合 `X`, 使得 `x in X` 当且仅当存在 `a in A` 和 `b in B`, 使得 `x = (a, b)`: `AA A AA B EE X AA x(x in X harr EE a EE b(a in A ^^ b in B ^^ x = (a, b)))`. 由外延公理可证集合 `X` 惟一, 称为 `A, B` 的 Descartes 积 (Descartes product), 记为 `X = A xx B := {(a,b): a in A, b in B}`.

因为 `a, b in A uu B`, 所以 `(a, b) := {{a},{a,b}} sube 2^(A uu B)`, 即 `(a, b) in 2^(2^(A uu B))`. 由子集公理, 集合 `X = {x in 2^(2^(A uu B)): EE a in A, EE b in B, x = (a, b)}` 存在.

二元关系

1. 设集合 `X, Y != O/`, 集合 `R sube X xx Y` 称为 `X` 到 `Y` 上的一个二元关系, 记作 `R: X to Y`. 显见 `R in 2^(X xx Y)`. 如果 `(x, y) in R`, 则称 `x, y` 是 `bm R`-相关的, 记为 `x R y`. 即 `x R y iff (x, y) in R`.
2. 分别称 `"dom"R = {x in X: EE y in Y, (x,y) in R} sube X`,
   `"ran"R = {y in Y: EE x in X, (x,y) in R} sube Y`,
   `"fld"R = "dom"R uu "ran"R` 为 `R` 的定义域 (domain), 值域 (range) 和域 (field).
   由定义知, `"fld" R = uuu(uuu R)`, `R sube "dom"R xx "ran"R sube "fld"R xx "fld"R`.
3. 定义二元关系 `R: X to Y` 的逆为: `R^-1 := {(y,x): (x,y) in R}`. `AA A sube "dom"R`, 定义 `A` 的截口 (section) 为: `R(A) := {y in Y: EE x in A, (x, y) in R}`, 特别 `R(X) = "ran"R`. 又定义单点集的截口为: `R(x) := {y in Y: (x, y) in R}`, `quad AA x in "dom"R`. 二元关系 `R: X to Z` 与 `S: Z to Y` 的复合为: `R @ S := {(x,y): EE z in Z, (x,z) in S and (z,y) in R}`. 换言之, `x, y` 有关系 `R @ S` 当且仅当存在中间元 `z`, 使得 `x S z` 且 `z R y`. 关系的复合满足结合律.

映射

映射的概念

1. 设集合 `X, Y != O/`, 考虑 `X` 到 `Y` 上的二元关系 `f`. 如果对任意 `x in X`, 都存在惟一的 `y in Y`, 使 `(x, y) in f`, 换言之, `X = "dom"f`, `quad (x,y) in f and (x,z) in f rArr y = z`, 换言之 `AA x in X`, `|f(x)| = 1`, 则称 `f` 为 `X` 到 `Y` 的一个 (良定义的) 映射 (mapping), 记为 `f: X to Y`.
   
2. 因为满足 `(x,y) in f` 的 `y` 是惟一的, 我们可以记 `y = f(x) iff (x,y) in f`. 此时称 `f` 把 `x` 映到 `y`, `y` 称为 `x` 在 `f` 下的像或像点, `x` 称为 `y` 在 `f` 下的一个原像.

在映射的定义中, 存在惟一性的条件也可以写成:
1. `(AA x in X)` `(EE y in Y)` `y = f(x)`;
2. `x_1 = x_2 rArr f(x_1) = f(x_2)`.

设 `f` 和 `g` 都是 `X` 到 `Y` 的映射, 由外延公理知 `f = g iff AA x in X, f(x) = g(x)`.

映射的像与核

设 `f: X to Y`, `A sube X`, `B sube Y`.
1. 称 `f(A) := {f(x): x in A} = {y in Y: (EE x in A) y = f(x)} sube Y` 为 `A` 在 `f` 下的像或像集. 约定 `f(O/) = O/`. 特别 `f(X) = "ran"f` 也记为 `"Im" f`, 称为 `f` 的像 (image).
2. 称 `f^-1(B) = {x in X: f(x) in B} sube X` 为 `B` 在 `f` 下的原像 (preimage)或原像集或完全原像. 单点集的原像可以简记 `f^-1({y}) = f^-1(y)`. 特别 `f^-1(Y) = "dom" f = X`.

设 `f: X to Y` 是映射, `A, A_1, A_2 sube X`, `B, B_1, B_2 sube Y`, `cc A sube 2^X`, `cc B sube 2^Y`. 又假定求交集时 `cc A, cc B != O/`, 则 `A_1 sube A_2 rArr f(A_1) sube f(A_2)`, `quad B_1 sube B_2 rArr f^-1(B_1) sube f^-1(B_2)`,
`f(uuu cc A) = uuu_(A in cc A) f(A)`, `quad f^-1(uuu cc B) = uuu_(B in cc B) f^-1(B)`,
`f(nnn cc A) sube nnn_(A in cc A) f(A)`, `quad f^-1(nnn cc B) = nnn_(B in cc B) f^-1(B)`,
`f(A_1\\A_2) supe f(A_1)\\f(A_2)`, `quad f^-1(B_1\\B_2) = f^-1(B_1)\\f^-1(B_2)`,
`f(X\\A) supe f(X)\\f(A)`, `quad f^-1(Y\\B) = X\\f^-1(B)`.

设 `f: X to Y`, 定义 `f` 的核 `"Ker" f = {(x_1, x_2) in X xx X: f(x_1) = f(x_2)}`. 换言之, `(x_1, x_2) in "Ker" f iff f(x_1) = f(x_2)`. 可以验证 `"Ker" f` 构成 `X` 上的一个等价关系 (见下文).

映射的复合与限制

设 `f, g` 为映射, 则按二元关系的复合, `f @ g` 也为一映射, 称为 `f` 与 `g` 的复合映射: `"dom"f @ g = "dom"g nn g^-1("dom"f)` `= {x in "dom"g: g(x) in "dom"f}`. 映射的复合也满足结合律.

定义集合 `X` 到自身的恒等映射或恒同映射为 `"id"_X: X to X`
`x mapsto x`. 恒等映射保持每一点不变.
容易验证, `(AA f: X to Y)` `f = f @ "id"_X = "id"_Y @ f`; `"Im"("id"_X) = X`, `"Ker"("id"_X) = Delta_X` (`X` 上最小的等价关系, 每个元素只和自身等价).

设 `f, g` 为映射. 如果 `f uu g` 还是一个映射, 亦即 `AA x in "dom"f nn "dom"g`, 都有 `f(x) = g(x)`, 则称 `f`, `g` 是相容的.
特别, 如果 `g sube f`, 即 `"dom"g sube "dom" f`, 且 `AA x in "dom"g, g(x) = f(x)`, 则称 `g` 为 `f` 的限制, `f` 为 `g` 的扩张. 记 `"dom"f = X`, `"dom"g = A sube X`, 则映射 `f: X to Y` 在子集 `A` 上的限制记为 `f|{::}_A: A to Y`
`x mapsto f(x)`. 容易验证 `f|{::}_A = f @ "id"_X|_A`, 其中 `"id"_X|_A` 称为包含映射.

满射, 单射, 双射

设 `f: X to Y`.
1. 如果对任意 `y in Y`, 都存在 `x in X`, 使得 `y = f(x)`, 则称 `f` 是满射 (surjection, onto);
2. 如果由 `f(x_1) = f(x_2)` 蕴含 `x_1 = x_2`, 则称 `f` 是单射 (injection, monophism, one-one);
3. 如果 `f` 既是单射又是满射, 则称 `f` 是双射 (bijection);

设 `f: X to Y`.
1. 以下各款等价:
   1. `f` 为一满射;
   2. `"Im" f = Y`;
   3. `(AA y in Y)` `|f^-1(y)| ge 1`;
   4. 存在右逆元 `g: Y to X`, 使 `f @ g = "id"_Y`.
   5. 满足右消去律: 对任意集合 `Z` 和任意 `g, h: Y to Z` 有 `g f = h f iff g = h`.
2. 以下各款等价:
   1. `f` 为一单射;
   2. `"Ker" f = iota_X` (`iota_X` 是 `X xx X` 上最小的等价关系, 每个元素只等价于自身);
   3. `(AA y in Y)` `|f^-1(y)| le 1`;
   4. 存在左逆元 `g: Y to X`, 使 `g @ f = "id"_X`.
      
   5. 满足左消去律: 对任意集合 `Z` 和任意 `g, h: Z to X` 有 `f g = f h iff g = h`.
3. 以下各款等价:
   1. `f` 为一双射;
   2. `(AA y in Y)`, `|f^-1(y)| = 1`;
   3. 存在左右逆元 `g: Y to X`, `g @ f = "id"_X`, `f @ g = "id"_Y`.
   4. 同时满足左右消去律.

`f` 为双射时, 对任意 `y in Y`, 存在唯一 `x in X` 使 `y = f(x)` (其存在性由满射保证, 唯一性由单射保证), 把这一对应关系记为 `f^-1`, 则 `f^-1` 是一个映射, 称为 `f` 的逆.

关于像集, 原像集和单射, 满射的关系, 我们有 (设 `A, B` 分别为 `X, Y` 的真子集): `f(f^-1(B)) sube B`, 等号成立当且仅当 `f` 为满射;
`f^-1(f(A)) supe A`, 等号成立当且仅当 `f` 为单射.

集合 `A` 到 `B` 有单射 `iff B` 到 `A` 有满射.

1. `rArr`: 设 `f: A to B` 是单射, `a_0` 是 `A` 中一个固定元素. 构造映射 `g: B to A`
   `b mapsto { f^-1(b), if b in f(A); a_0, otherwise :}` 容易看出 `g(f(a)) = a`, 因此 `g` 是满射.
2. `lArr`: 反向的证明依赖选择公理. 设 `g: B to A` 是满射, 因此对任意 `a in A`, 原像 `g^-1(a) := { b in B: g(b) = a }` 非空. 由选择公理, 可以从每个原像中选出一个元素, 令它等于 `f(a)`, 从而定义映射 `f: A to B`
   `a mapsto f(a) in g^-1(a)` 容易看出 `g(f(a)) = a`, 因此 `f` 是单射.

特征函数

设 `f: X to Y`. 当 `Y = X` 时, 又称 `f` 为 `X` 上的变换. 当 `Y = RR` 时, 又称 `f` 为函数.

设 `A sube X`, 定义特征函数 `chi_A: X to {0, 1}` 如下: `chi_A(x) = { 1, if x in A; 0, if x in X\\A; :}` 一定意义上特征函数可以代表集合 `A` 本身. 如 `A = B iff chi_A = chi_B`, `quad A sube B iff chi_A le chi_B`. 关于特征函数与集合运算之间的联系, 我们有 `chi_(A^c)(x) = 1 - chi_A(x)`
`chi_(A nn B)(x) = chi_A(x) * chi_B(x)`
`chi_(A \\ B)(x) = chi_A(x)(1 - chi_B(x))`
`chi_(A uu B)(x) = chi_A(x) + chi_B(x) - chi_A(x) * chi_B(x)`
`chi_(A /_\ B)(x) = |chi_A(x) - chi_B(x)|`

等价关系

设 `R` 是一个二元关系, 满足:
1. 自反性. `AA x in X`, `x R x`;
2. 对称性. `x R y rArr y R x`;
3. 传递性. `x R y and y R z rArr x R z`.
则称 `R` 为 `X` 上的一个等价关系. `AA x in X`, 称 `R(x) = {y: x R y}` 为 `x` 的等价类.

若关系 `R` 是对称的和传递的, 则它是一等价关系.

`AA x in "dom"R`, `EE y in "ran"R`, `x R y`. 由对称性, `y R x`. 再由传递性有 `x R x`, 即 `R` 是自反的.

设 `R` 为一等价关系, 则由对称性得到 `"dom"R = "ran"R`.

设 `R` 是 `X` 上一个等价关系, 则 `(x,y) in R rArr R(x) = R(y)`, `quad (x,y) !in R rArr R(x) nn R(y) = O/`. 于是任意两个等价类要么重合, 要么不相交. 这样 `X` 就被划分为一些不相交等价类的并, 换言之, 集合 `X//R := {R(x): x in X}` 构成 `X` 的一个划分 (partition), 称 `X//R` 为 `X` 模 `R` 的商集.

`AA z in R(x)`, 有 `(x,z) in R`, 如果 `(x,y) in R`, 由对称性和传递性得到 `(y,z) in R`, 即 `z in R(y)`. 于是 `R(x) sube R(y)`. 同理 `R(y) sube R(x)`.
假设 `EE z in R(x) nn R(y)`, 有 `(x,z), (y,z) in R`. 由对称性和传递性得到 `(x,y) in R`, 矛盾.

若 `cc D` 是 `X` 的一个划分, 可以确定 `X` 上的等价关系 `R`: `x_1 R x_2 iff EE D in cc D, x_1, x_2 in D`. 此时 `cc D` 中的每个集合都是一个等价类, 于是 `R(x)` 确定了 `X` 到 `D` 上的一个满射.
反之若 `f` 是满射, 则商集 `X//"Ker"f = {f^-1(y): y in Y}` 与 `Y` 之间存在双射.

序结构

预序, 偏序, 全序

设二元关系 "`le`" 满足:
1. 自反性. `AA x in X`, `x le x`;
2. 传递性. `x le y and y le z` `rArr x le z`.
则称 `(X, le)` 是一个预序 (preorder) 集. 若它还满足
3. 反对称性. `x le y and y le x` `rArr x = y`;
则称 `le` 为一偏序 (partial order), `(X, le)` 为 `X` 上的偏序集. 若它进一步满足
4. 任意元素都可以比较大小. `AA x, y in X`, `x le y or y le x`.
则称 `le` 为 `X` 上的全序 (total order) 或线序.
偏序集的子集自然继承了偏序结构: `C sube X`, 则 `(C, le) := (C xx C) nn le`.
偏序集 `X` 的子集 `C` 如果是全序, 则 `C` 称为 `X` 的一条链.

我们记 `x ge y iff y le x`,
`x lt y iff x le y and x != y`,
`x gt y iff x ge y and x != y`. 在全序集中, 对任意元素 `x, y`, 三命题 `x lt y`, `x = y` 或 `x gt y` 恰有一个成立.

1. 实数集是全序集.
2. 正整数的整除、集合的包含, 都是偏序的例子.
3. [来自群友 墨花雪月] 整数集 `ZZ` 配上整除关系构成预序. 因为 2 与 -2 互相整除但不相等, 所以不满足反称性.
4. [来自群友 壹零叁] 平面 `RR^2`, 规定 `(x,y) le (z,w) iff x le z`, 则这构成一个预序.

最大, 极大; 上界, 上确界

设 `(X, le)` 为一预序集, 非空集 `E sube X`.
1. 称 `m in X` 为 `E` 的一个上界 (upper bound), 如果 `AA x in E, x le m`.
2. 称 `m` 为 `E` 的一个最大元, 如果 `m in E`, 且 `m` 为 `E` 的一个上界. `E` 的最大元记为 `max E`.
3. 称 `m` 为 `E` 的一个极大元, 如果 `m in E`, 且不存在 `x in E` 使得 `x gt m`. 换言之, `AA x in E`, `x ge m rArr x = m`.
4. 称 `s` 为 `E` 的一个上确界, 如果 `s` 是 `E` 的最小上界, 即 `s` 是 `E` 的上界, 且对任意上界 `m` 有 `s le m`. `E` 的上确界记为 `Sup E`.
类似可以定义下界, 最小元 (`min E`), 极小元和下确界 (`inf E`).

在全序集中, 极大元就是最大元.

在偏序集中, 由反对称性知道, 最大元若存在, 必惟一, 且为一极大元. 同理在偏序集中, 上 (下) 确界若存在, 必惟一.

称预序集 `(X, le)` 是 (序) 完备的, 如果它满足确界原理: (1) 任意有上界的子集必有上确界; (2) 任意有下界的子集必有下确界.

确界原理的两个条件相互等价.

我们证明 (1) `rArr` (2). 设 `(X, le)` 任意有上界的子集都有上确界, 设非空集 `E sube X` 有下界. 下证 `E` 有下确界.
1. 令 `A` 是 `E` 的全体下界, 则 `A` 不空, 且 `AA e in E, AA a in A`, 由 `a` 是 `E` 的下界有 `a le e`, 从而 `E` 的任一元都是 `A` 的上界.
2. 令 `a = "sup"A`, 则由 `a` 是 `A` 的最小上界知, `AA e in E`, `a le e`, 从而 `a` 是 `E` 的下界, 即 `a in A`. 我们已经证明 `a` 是 `A` 的最大元, 即为 `E` 的最大下界, 所以 `a = "inf"E`, 从而 `E` 有下确界.

格 (lattice)*

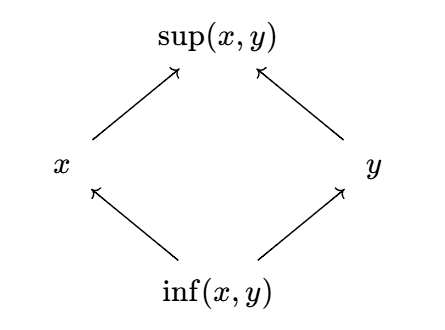
若偏序集 `(X, le)` 中任意一对元素 `x, y` 都存在上确界和下确界, 则称 `X` 是格序集 (lattice ordered set). 显然全序集是格序集.

在格序集中, 下列命题等价: `x le y iff inf(x, y) = x iff Sup(x, y) = y`. 换言之, 如果 `x, y` 不能比较大小, 那么必存在元素 `inf(x, y)` 和 `Sup(x, y)`, 使左下的图形成立. 右下是格序集 `(ZZ^+, 整除)` 的部分图形.

1. `(RR, le)` 是格序集, 它的上、下确界运算分别是 `max, min`.
2. `(ZZ^+, 整除)` 是格序集, 上、下确界是 `lcm, gcd`.
3. `(集合的幂集, sube)` 是格序集, 上、下确界是 `uu, nn`.

设有三元组 `(L, ^^, vv)`, `L` 是集合, `^^` (vee), `vv` (wedge) 是 `L` 上的二元运算. 且对任意 `x, y, z in L` 满足:
1. 交换律: `x ^^ y = y ^^ x`, `x vv y = y vv x`;
2. 结合律: `(x ^^ y) ^^ z = x ^^ (y ^^ z)`, `(x vv y) vv z = x vv (y vv z)`;
3. 吸收律: `x ^^ (x vv y) = x vv (x ^^ y) = x`;
则称 `(L, ^^, vv)` 是代数格 (algebraic lattice).

由吸收律推出幂等律: `x ^^ x = x vv x = x`.

只证第一个等号. `x ^^ color(red)(x)` `= x ^^ (color(red)(x vv (x ^^ x)))` `= x`.

可以验证, 格序集 `(X, inf, Sup)` 满足代数格的定义; 另一方面, 在代数格 `(L, ^^, vv)` 上定义 `x le y iff x ^^ y = x`, 那么 `(L, le)` 是格序集. 因此我们不再区别格序集和代数格, 而是统称为格 (lattice).

分配律 在格中, 下面两条等价:
1. `AA x, y, z`, `(x ^^ y) vv z = (x vv z) ^^ (y vv z)`;
2. `AA x, y, z`, `(x vv y) ^^ z = (x ^^ z) vv (y ^^ z)`.

只证 1 `rArr` 2. 右边 `= (x ^^ z) vv (y ^^ z)`
`= (x vv (y ^^ z)) ^^ (z vv (y ^^ z))`
`= (x vv y) ^^ (x vv z) ^^ z`
`= (x vv y) ^^ z` `=` 左边.

1. [来自群友 103] 存在不满足分配律的格. 比如五元集 `{0, a, b, c, 1}` 的序定义如下: `0` 最小, `1` 最大, `a, b, c` 之间不可比较. 计算知 `(a ^^ b) vv c` `= 0 vv c = c`,
   `(a vv c) ^^ (b vv c)` `= 1 ^^ 1` `= 1`.
   
   然而, 存在弱化版本的定理: `x le z and y ≤ z rArr x vv y le z`; 即 `x ^^ z = x and y ^^ z = y rArr (x vv y) ^^ z = (x ^^ z) vv (y ^^ z)`.
2. [来自群友 无懈可击99] 一个希尔伯特空间的所有闭子空间 (特别地, 一个有限维线性空间的所有线性子空间) 组成一个格, 它没有分配律.

保序映射; 区间

设 `(X, le)`, `(Y, ≼)` 是预序集.
1. 称 `f: X to Y` 为保序映射, 如果 `x_1 le x_2 rArr f(x_1) ≼ f(x_2)`.
2. 称 `f: X to Y` 为严格增的, 如果 `x_1 lt x_2 rArr f(x_1) ≺ f(x_2)`. 全序集之间的严格增映射为单射.
3. 若 `f` 是双射, 且 `f` 和 `f^-1` 皆保序, 则称 `f` 是 `X` 到 `Y` 的一个序同构, 记作 `(X, le) ~ (Y, ≼)`. 对于序同构我们有 `x le y iff f(x) le f(y)`, 特别对于全序集之间的同构有 `x lt y iff f(x) lt f(y)`, 即全序集同构都是严格增的.
偏序集的同构类称为序型, 如果 `X` 和 `Y` 序同构, 则它们是相同序型.

设 `(X, le)` 为一全序集, `a, b in X`, 定义以 `a, b` 为端点的闭区间和开区间分别为 `[a,b] := {x in X: a le x le b}`, `quad (a, b) := {x in X: a lt x lt b}`. 若 `(a, b) = O/`, 就称 `(a, b)` 是 `X` 的一个间隙 (gap). 称 `E sube X` 为一区间, 如果 `AA x, y in E`, `[x, y] sube E`. 如果对任意不空的开区间 `(a, b)`, 有 `(a, b) nn E != O/`, 则称 `E` 是(序) 稠密的.

若偏序集 `X` 非空, 且对任意 `x, y in X`, 子集 `{x, y}` 都有上界, 则称 `X` 是滤过序集. 显然全序集皆是滤过的, `max{x, y}` 就是 `{x, y}` 的一个上界.

良序

(G. Cantor) 若全序集 `P` 的任意非空子集都有极小元, 则称它为良序集. 例如, 正整数集是良序集, 实数集 `RR` 则不是. 良序集的子集仍是良序集.

空集也是良序集 (反正它没有非空子集, 可以耍赖).

子列引理 设 `P` 为良序集, 映射 `f: P to P` 严格增, 则对每个 `x in P` 有 `f(x) ge x`. 例如 `{a_(n_k)}` 是数列 `{a_n}` 的子列, 映射 `k mapsto n_k` 严格增, 那么就有 `n_k ge k`.

假设集合 `P_0 := { x in P: f(x) lt x }` 非空, 取 `P_0` 的极小元 `z`, 则 `f(z) lt z`, 由 `f` 严格增可知 `f(f(z)) lt f(z)`, 即 `f(z) in P_0`. 这与 `z` 的极小性矛盾.

1. 良序集仅有平凡的自同构.
2. 设 `P` 为良序集, `P_(lt x) := { y in P: y lt x }` 称为 `P` 的一个前段. 上述引理告诉我们, 对任意 `x in P`, `P` 与 `P_(lt x)` 不同构.

1. 设 `f` 是良序集 `P` 的自同构, 由于全序集的同构都是严格增的, 所以 `f, f^-1` 都严格增. 由引理, 对于任意 `x in P`, `f(x) ge x`, `x = f^-1(f(x)) ge f(x)`, 所以 `f(x) = x`.
2. 如果存在 `P` 到 `P_(lt x)` 的同构 `f`, 由于全序集的同构都是严格增的, 所以 `f` 严格增. 然而 `f(x) lt x`, 一个矛盾.

顾名思义, 良序集的性质十分优良. 设 `P` 是良序集, 取出它的极小元 `x_0` 后, 剩下的 `P\\{x_0}` 中又可取出一个极小元 `x_1`, 如此进行下去, 良序集可以排列成一行: `x_0, x_1, cdots`. 当然这种排列不一定唯一, 且良序集的序结构未必就和自然数集一样, 理应存在比自然数集更大的良序集. 我们不禁疑问, 良序集的序型到底有多少种呢, 能否从每一种序型中选出一个典型代表? 这就是下篇介绍的序数.