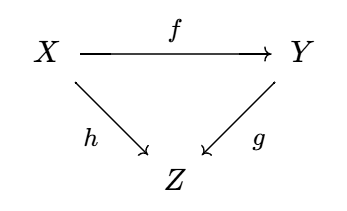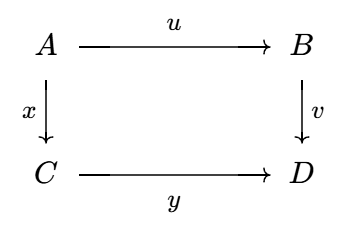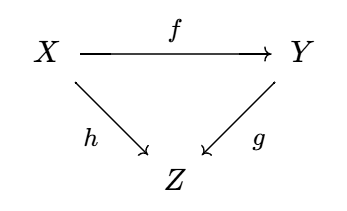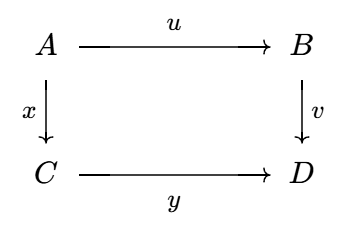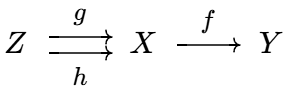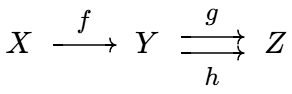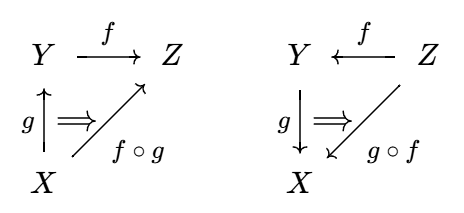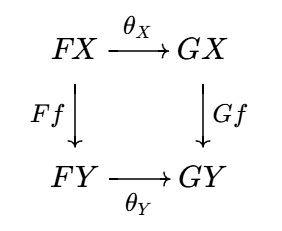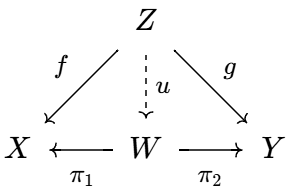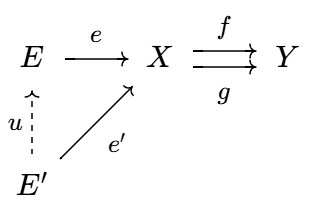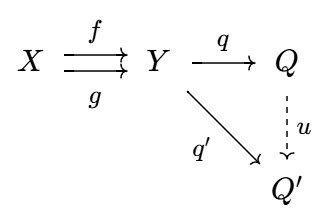概括来说:
  1. 范畴 (category)是由对象及其间的态射组成的: `X overset f to Y`. 这里 `X, Y` 是对象, `f` 是态射.
  2. 函子 (functor)则是范畴间保持箭头结构的“映射”: `cc C overset F to cc D`. 这里 `cc C, cc D` 是范畴, `F` 是函子.
  3. 自然变换描述了函子之间的关系: `F overset theta to G`, 这里 `F, G` 是函子, `theta` 是自然变换.
    4. 箭头图表在范畴论中随处可见, 但箭头可以有以上几种不同的含义, 需根据上下文加以辨析.

范畴

范畴的定义

形象地说, 范畴是一个有向图, 图中的顶点称为对象, 有向边称为态射. 具体定义如下:

    一个范畴 (category) `cc C` 由它的对象集合 `"Ob"(cc C)` 和态射集合 `"Mor"(cc C)` 组成, 此外还应满足:
  1. 边与点的关系 `cc C` 中任意态射 `f` 都有确定的来源与目标对象.
    换言之有来源映射和目标映射 `s, t: "Mor"(cc C) to "Ob"(cc C)`. 若 `f` 是一个态射, 那么 `X := s(f)`, `Y := t(f)` 都是对象, `f` 称为从 `X` 到 `Y` 的态射, 记为 `X overset f to Y` 或 `f: X to Y`.
  2. 点与边的关系 `cc C` 中任意两个对象 `X, Y` 确定了一族态射.
    将全体从 `X` 到 `Y` 的态射称为 `(X, Y)` 的 Hom 集: `Hom_C(X, Y) := s^-1(X) nn t^-1(Y)`. 因此 `f: X to Y` 的另一种写法是 `f in Hom_C(X, Y)`.
  3. 态射的合成与恒等态射 设 `f: X to Y`, `g: Y to Z`, 定义 `f, g` 的二元合成为 `f @ g`: `X to Z`, 或简记为 `f g`. 对每个对象 `X`, 都存在态射 `"id"_X: X to X`, 称为 `X` 到自身的恒等态射. 态射的合成满足: `f(g h) = (f g)h quad` (结合律)
    `f @ "id"_X = f = "id"_Y @ f quad`(恒等态射的性质).     恒等态射的性质保证了 `"id"_X` 的唯一性.

`X in "Ob"(cc C)` 简记为 `X: cc C`.

  1. 态射的逆 设态射 `f: X to Y`, 若存在 `g: Y to X` 使得 `f g = "id"_Y`, `g f = "id"_X`, 则称 `g` 是 `f` 的逆, `f` 是可逆态射或同构. `X` 到 `Y` 的全体同构记为 `"Isom"_(cc C)(X, Y)`. 由恒等态射的性质知道, 逆若存在则必唯一.
  2. 简记 `"End"_(cc C)(X) := Hom_C(X, X)`, `"Aut"_(cc C)(X) := "Isom"_(cc C)(X, X)`, 分别称为 `X` 的自同态集和自同构集. `"End"(X)` 是幺半群, `"Aut"(X)` 是群.
  3. 对象集和态射集皆空的范畴称为空范畴, 记为 `bb 0`.
  1. 幺半群 (Monoid) 上也有二元合成, 且满足结合律, 并带有单位元. 与范畴的区别在于, 幺半群只有一个单位元, 而范畴中的恒等态射可以有许多——每个对象都带有一个恒等态射. 这种意义下范畴是幺半群的推广, 而幺半群相当于只有一个对象的范畴, 因此我们也把只有一个对象的范畴叫做 monoid.
  2. 如果一个 monoid 的所有态射都可逆, 那么它其实是群, 此时群的元素是范畴的态射, 群的乘法是态射的合成. 推而广之, 把所有态射都可逆的范畴称为群胚 (groupoid) 或广群.

以字母表示对象, 箭头表示态射, 范畴可以用箭头图表很好地可视化. 如果图表中的箭头合成殊途同归, 我们就说它是交换的, 故箭头图表又称为交换图表. 比如下图就有 `g f = h` 和 `v u = y x`. 这些图表可以用 quiver 在线绘制.

条条大路通罗马，所以交换图表是不是也可以叫做罗马表（

子范畴、反范畴、积范畴

范畴的例子

"全体集合" 这个概念太大, 已不是一个集合. 为了适用范畴的定义, 我们总是事先取定一个宇宙 `cc U`, 以下的集合、群、拓扑空间等, 都是在这个宇宙中进行讨论的.

  1. 集合范畴 `sf(Set)`: 对象为 (某个宇宙中的) 所有集合, 态射为集合间的映射.
  2. 群范畴 `sf(Grp)`: 对象为所有群, 态射为群同态.
  3. 交换群范畴 `sf(Ab)`: 对象为所有交换群, 态射为群同态, 它是 `sf(Grp)` 的全子范畴.
  4. 域 `bbb k` 上的向量空间范畴 `sf(V ect)(bbb k)`: 对象为 `bbb k` 上所有向量空间, 态射为线性映射. 类似定义有限维向量空间范畴 `sf(V ect)_(f)(bbb k)`, 它是 `sf(V ect)(bbb k)` 的全子范畴.
    5. 总之, 有一大类范畴, 其对象是一些带有代数运算的集合, 态射则是集合之间保持这些运算的映射, 即同态. 这样的范畴还有环范畴 `sf(Ri ng)`, 无幺环范畴 `sf(Rng)`, 交换环范畴 `sf(CRi ng)`, 环 `R` 上的左模范畴 `sf(Mod)_R` 等等. 下面的例子表明, 范畴中的态射不必是映射:
  5. 关系范畴 `sf(Rel)`: 对象为全体集合, `"Hom"(X, Y)` 是集合 `X, Y` 之间的全体二元关系. 态射合成定义为 `tau @ sigma := { (x, z): (x, y) in sigma and (y, z) in tau} }`.
  6. 拓扑空间范畴 `sf(To p)`: 对象为所有 Hausdorff 拓扑空间, 态射为连续映射. 类似定义带基点的拓扑空间范畴 `sf(To p)^ast`.
  7. 给定集合, 可以定义相应的离散范畴 `sf(Disc)(S)`: 对象集为 `S`, 态射仅有恒等态射 `{"id"_x: x in S}`.
  8. 域 `K` 上的矩阵范畴 `M_K`: 对象为全体正整数, 态射 `A: m to n` 是 `m xx n` 矩阵, 态射的合成为矩阵乘法: `A @ B := B A`.
  9. 偏序范畴 设 `{s}` 是一个单点集, `(A, le)` 是偏序集. 定义偏序范畴 `cc A` 如下: 对象 `"Ob"(cc A) = A`. 态射 `"Hom"(X, Y) := {{s}, if X le Y; O/, otherwise:}`. 换言之, 如果 `X le Y`, 就在它们之间连一个箭头, 否则它们之间没有箭头. 态射的合成是平凡的: `s @ s = s`. 偏序范畴的图表和 Hasse 图是一致的.

单态射与满态射

    设 `X, Y: cc C`, `f: X to Y`.
  1. 称 `f` 为单态射, 如果它满足左消去律: 对任意 `Z: cc C` 和任意 `g, h: Z to X` 有 `f g = f h iff g = h`.
  2. 称 `f` 为满态射, 如果它满足右消去律: 对任意 `Z: cc C` 和任意 `g, h: Y to Z` 有 `g f = h f iff g = h`.
  3. 称 `f` 左可逆, 如果存在 `g` 使得 `g f = "id"_X`; 称 `f` 右可逆, 如果存在 `g` 使得 `f g = "id"_Y`. 一个态射可逆当且仅当它左右皆可逆.
    4. 将所有箭头掉转, 单态射与满态射就可以互相转化, 因此单态射在反范畴里是满态射, 而满态射在反范畴里是单态射.

助记: 单态射的定义 `f g = f h iff g = h` 与集合论中单射函数的定义 `f(x) = f(y) iff x = y` 神似.

左可逆蕴涵单, 右可逆蕴涵满. 因此同构既是单态射又是满态射.

设 `f` 左可逆, 从等式 `f g = f h` 两边同乘以 `f` 的左逆就得到 `g = h`.

在集合论意义下, 单态射等价于左可逆 (单射函数), 满态射等价于右可逆 (满射函数). 范畴论中则未必: 在有些范畴中如 `sf(Set)`, `sf(Grp)`, `sf(Mod)_R`, `sf(V ect)(bbb k)` 中它们是等价的, 但在 `sf(To p)` 中, 态射有稠密的像便是满态射. 又如 `sf(Ri ng)` 中, 单态射就是单的环同态, 然而满态射不等同于满的环同态, 例如从 `ZZ to QQ` 的包含同态是满态射, 但不是满射函数.

  1. 设 `f` 是集合间的单态射, 取 `g, h` 为常值映射 `g: z mapsto x_1`, `h: z mapsto x_2`. 于是 `f(x_1) = f(x_2)` `rArr f g = f h` `rArr g = h` `rArr x_1 = x_2`. 这证明了 `f` 是单射函数.
  2. 又设 `g f = h f rArr g = h`, 反设 `f` 不是满射函数, 则 `EE y_0 in Y - f(X)`. 我们可以让 `g(y), h(y)` 在 `y in f(X)` 时相等, 但 `g(y_0) != h(y_0)`. 此时 `g f = h f` 但 `g != h`, 矛盾.
  3. 假如 `g, h` 是拓扑空间之间的连续映射, `g f = h f`, 此时 `g, h` 在 `f` 的像集上相等. 但 `f` 有稠密的像, 所以 `g, h` 处处相等. 因此 `f` 是满态射.
  4. 设 `R` 为一环, 同态 `f: ZZ to QQ`, `g, h: QQ to R`, 且 `g f = h f`. 同样 `g, h` 在 `f` 的像集上, 即在自变量为整数时相等. 我们要求同态保持幺元 1, 从而对任意正整数 `n in QQ`, `g(1//n) g(n)` `= g(n) g(1//n)` `= g(n * 1//n)` `= g(1)` `= 1 in R`. 因此 `g(1//n)` 是 `g(n)` 在环 `R` 中的逆. 同理 `h(1//n)` 是 `h(n)` 的逆. 但 `g(n) = h(n)`, 由逆元唯一性知道 `g(1//n) = h(1//n)`. 从而对任意 `a in QQ` 成立 `g(a) = h(a)`. 因此 `f` 是满态射.
  5. 模范畴 `sf(Mod)_R` 中单、满态射分别等价于单同态、满同态的证明: 设 `f` 是单同态, 则它是集合间的单射函数, 从而是单态射. 现在设 `f` 是单态射, 考察正合列 `"Ker" f overset i to A overset f to B`, 其中 `"Im" i = "Ker" f`, 即 `f i = 0` (零同态). 由 `f` 是单态射知道, `f i = 0 = f 0` `rArr i = 0`, 从而 `"Ker" f = 0`, `f` 是单同态.
    又设 `f` 是满同态, 则它是集合间的满射函数, 从而是满态射. 现在设 `f` 是满态射, 考察正合列 `A overset f to B overset pi to B//"Im"f`, 其中 `"Im" f = "Ker" pi`, 即 `pi f = 0`. 由 `f` 是满态射知道, `pi f = 0 = 0 f` `rArr pi = 0`, 从而 `"Im"f = B`, `f` 是满同态.
  6. 群范畴 `sf(Grp)` 中单态射与单同态的等价性证明与模范畴完全类似. 但在证明满态射与满同态的等价性时, 会遇到困难: `"Im"f` 不一定是 `B` 的正规子群. 这部分完整证明参见 知乎专栏: 模与范畴.
    子对象与商对象 设 `cc C` 为范畴, `A: cc C`.
  1. 考虑终点在 `A` 的所有单态射构成的类, 在这个类上定义二元关系 `le`: `f le g iff (EE k) f = g k`. 由定义知 `k` 也是单态射. 规定等价关系 `f -= g iff f le g and g le f`, 我们将其导出的等价类称为 `A` 的子对象.
  2. 对偶地, 考虑从 `A` 出发的所有满态射构成的类, 定义 `ge`: `f ge g iff (EE k) f = k g`, 规定等价关系 `f -= g iff f ge g and g ge f`, 其导出的等价类称为 `A` 的商对象.
  1. 注意, 子对象和商对象是态射的等价类, 不是对象的等价类.
  2. 容易看出, 当 `k` 为同构时, 上述的 `f` 和 `g` 就是等价的.
  3. 考虑群范畴 `sf(Grp)` 的商对象. 相差一个同构的意义下, 从 `A` 出发的一个满态射 `f` 决定了 `A` 的一个商群 `A // "Ker" f`. 再考虑其子对象. 若群 `B` 到 `A` 存在一个嵌入, 则 `B` 同构于 `A` 的一个子群. 因此群范畴的商对象与子对象恰好是商群与子群 (相差一个同构).

函子与自然变换

函子

函子是范畴到范畴的 "态射", 它将一个交换图表映为另一个交换图表.

可以将函子对态射的作用类比于幺半群的同态: `f(a b) = f(a) f(b)` 和 `f(1) = 1`. 不过如前所述, 范畴中的恒等态射和对象一样多, 但幺半群的单位元只有一个.

函子保持左、右可逆态射, 但不一定保持单态射和满态射. 例如, 设 `M, N` 为幺半群, 视它们为单个对象的范畴. 则函子 `F: M to N` 就是幺半群同态. 特别令 `M = (NN, +)`, `N = ({0, 1}, max)`, `F(m) = min(1, m)`, 则 `1` 在 `M` 中是单态射也是满态射, 在 `N` 中则都不是.

  1. 函子的合成 设 `F: cc C_1 to cc C_2`, `G: cc C_2 to cc C_3`, 将它们对象间与态射间的映射分别合成, 就得到合成函子 `G @ F`. 函子的合成满足结合律.
  2. 反变函子 形如 `cc C to cc D` 的函子称为共变函子, `cc C^"op" to cc D` 称为反变函子. 反变函子的定义在对象层次与前相同, 在态射层次则反转箭头方向, 即 `Hom_C(X, Y) to Hom_D(F Y, F X) quad` (反转箭头),
    `F(f g) = F(g) F(f) quad` (反向合成).     由于反范畴与范畴只在箭头方向上不同, 函子 `cc C to cc D` 和 `cc C^"op" to cc D^"op"` 是一回事, `cc C^"op" to cc D` 和 `cc C to cc D^"op"` 也是一回事.
    对于函子 `F: cc C to cc D`,
  1. 在对象层次, 称 `F` 是本质满或稠密的, 若 `cc D` 中任一对象都同构于某个 `F X`. 这是把满射定义中的 "等于" 换成了 "同构于".
  2. 在态射层次, 称 `F` 是忠实的 (faithful), 若 `Hom_C(X, Y) to Hom_D(F X, F Y)` 都是单射. 称 `F` 是完全的 (或全的, full), 如果上述映射都是满射. 既忠实又全的函子称为全忠实的.

忠实是比单射弱的一个概念. 可能出现这样的情况: `X, Y, Z` 是 `cc C` 的不同对象, 但 `F Y = F Z`, 这时一个忠实的函子允许箭头 `X to Y` 和 `X to Z` 被映到同一个箭头. 同理 "全" 是比满射弱的概念.

设 `cc C` 是范畴, `f: A to B`. 若 `F: cc C to cc D` 是全忠实函子, 且 `F(f)` 是单同态/满同态/有左逆/有右逆/是同构, 则 `f` 也同样如此.

  1. 设 `cc C` 为 `cc D` 的子范畴, 则包含函子 `iota: cc C to cc D` 是忠实的, 它在对象和态射层次都是包含映射; 它是全忠实的当且仅当 `cc C` 是 `cc D` 的全子范畴.
  2. 忘却函子 (遗忘函子, forgetful functor) 忘却环的乘法, 可以将它视为加法群; 忘却所有结构便得到底层的集合. 在对象层次, 这些函子忘却一部分的代数结构 (环的乘法、向量空间的纯量乘法...), 在态射层次, 这些函子化为箭头之间的包含映射. 比如 `sf(Ri ng)` 到 `sf(Ab)` 的忘却函子就把两个环 `R, R'` 之间的环同态映为两个加法群的群同态. 忘却函子都是忠实的.
  3. 基本群 (一阶同伦群) 函子 设 `X` 是拓扑空间, `x in X`, 则 `pi_1(X, x)` 代表 `X` 在 `x` 这一点的基本群. 可以验证 `pi_1: sf(To p)^ast to sf(Grp)` 是函子.
  4. 幂集函子 `cc P: sf(Set) to sf(Set)` 将集合 `A` 映为幂集 `cc P(A)`, 态射 `f: A to B` 映为 `cc P(f): cc P(A) to cc P(B)`. 具体而言, `cc P(f)` 将子集 `A_1 sube A` 映为它的像 `f(A_1) sube B`.
  5. `n` 阶矩阵函子 `M_n: sf(Ri ng) to sf(Ri ng)` 和 `n` 阶可逆矩阵函子 `GL_n: sf(Ri ng) to sf(Grp)`. 它们分别将环 `R` 映为 `R` 上的全体 `n` 阶矩阵和 `n` 阶可逆矩阵.
  6. Abel 化函子 `Ab: sf(Grp) to sf(Ab)` 将群 `G` 映为一个 Abel 群 `G//G'`, 其中 `G'` 是 `G` 的导群 (又称换位子群). 代数学中还有众多的标准处理可以描述为函子: 半群的群化、环的局部化等等.
  7. 积范畴到分量的投影函子 `P: cc C xx cc D to cc C`. 它将对象 `(A, B)` 映为 `A`, 态射 `(f, g)` 映为 `f`. 范畴到积范畴的对角函子 `"Dia": cc C to cc C xx cc C`. 它将对象 `A` 映为 `(A, A)`, 态射 `f` 映为 `(f, f)`.
在函数式编程中, 函子常见于容器间的映射. 例如 map 将一个数组映为另一个数组: map (+1) [1,2,3] 得到 [2,3,4],
map square [1,2,3] 得到 [1,4,9]. 这里 map 是 Int 范畴到 Array Int范畴的函子. 它同样满足函子对态射的性质: 
map identity = identity
(map g) ∘ (map f) = map (g ∘ f)

Hom 函子 给定范畴 `cc C` 及其对象 `X`, 定义协变 Hom 函子 `"Hom"(X, *): cc C to sf(Set)`,
(对象层次) `Y mapsto "Hom"(X, Y)`,
(态射层次) `f mapsto "Hom"(X, f)`, 其中 `f: Y to Z`, `"Hom"(X, f): "Hom"(X, Y) to "Hom"(X, Z)` `:= g mapsto f g`. 同理定义反变 Hom 函子 `"Hom"(*, X): cc C^"op" to sf(Set)`
(对象层次) `Y mapsto Hom_C(Y, X)`,
(态射层次) `f mapsto "Hom"(f, X)`, 其中 `f: Z to Y`, `"Hom"(f, X): Hom_C(Y, X) to Hom_C(Z, X)` `:= g mapsto g f`. 两个函子互为对偶. 助记: `"Hom"(X, f) = f @`, `"Hom"(f, X) = @ f`.

自然变换

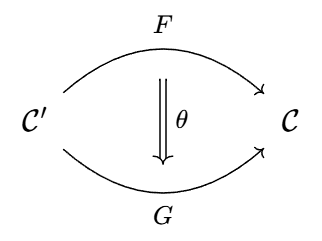
自然变换 设函子 `F, G: cc C to cc D`. 从 `F` 到 `G` 的自然变换 `theta: F rarr G` 定义为一族态射 `theta = { theta_X: F X to G X | X: cc C }`, 且对所有态射 `f: X to Y` 满足 `theta_X @ G f = F f @ theta_Y`. 下面是两种常见的图解, 验证自然变换, 关键是验证下面的图表交换:
自然变换1
自然变换2
  1. 自然变换的合成 `theta: F to G` 和 `psi: G to H` 的合成定义为 `psi theta: F to H`, 使得 `(psi theta)_X = psi_X theta_X`. 合成运算满足结合律. `F(X) to G(X) to H(X)`
    `darr qquad qquad darr qquad qquad darr`
    `F(Y) to G(Y) to H(Y)`
  2. 自然变换乘函子 对 `theta: F_1 to F_2` 左乘或右乘一个函子, 可以得到两个新的自然变换: `theta G := {theta_(G Y)}_Y: F_1 G to F_2 G`,
    `H theta := {H theta_X}_X: H F_1 to H F_2`.     当然, 前提是函子的合成 `F_1 G`, `F_2 G`, `H F_1`, `H F_2` 有意义. 我们有结合律 `(H theta) G = H (theta G)`. `F_1 G(X) to F_2 G(X)`
    `darr qquad qquad darr`
    `F_1 G(Y) to F_2 G(Y)`
  1. 记函子 `F: cc C to cc D` 到自身的恒等变换为 `"id"_F := { "id"_(F X) | X: cc C }`.
  2. 若 `theta: F to G` 中的态射皆为同构, 则称 `theta` 是自然同构, 定义其逆 `theta^-1: G to F` 为 `theta^-1 := { theta_X^-1 | theta_X in theta }`. 可以验证 `theta^-1 theta = "id"_F`, `theta theta^-1 = "id"_G`. 若 `theta` 是自然同构, 则它乘以函子后 `theta G, H theta` 也是同构.
    双重对偶空间 自然变换的一个典型例子是向量空间到其双重对偶空间的自然同态. 考虑 `bbb F` 上的向量空间 `V`, 它的对偶空间 `V^ast` 由全体 `V` 到 `bbb F` 的线性函数组成.
  1. 定义对偶函子 (duality functor) `D` 如下 `D: sf(V ect)(bbb F)^"op" to sf(V ect)(bbb F)`
    (对象层次) `V mapsto V^ast`
    (态射层次) `A mapsto A^ast`.     其中 `A: V to W` 为线性映射, `A^ast` 为对偶线性映射: `A^ast: W^ast to V^ast` `:=` `f mapsto f A`. 由于 `(A B)^ast = B^ast A^ast`, `"id"_V^ast = "id"_(V^ast)`, 所以 `D` 是反变函子. 同理可构造另一个反变函子 `D^"op" = sf(V ect)(bbb F) to sf(V ect)(bbb F)^"op"`.
  2. 记 `"id"_(sf(V ect)(bbb F))` 是恒等函子, `D D^"op"` 是双重对偶函子. 定义自然变换 `theta: "id"_(sf(V ect)(bbb F)) to D D^"op"`, 其中 `theta_V: V to V^(ast ast)` `:=` `v mapsto f mapsto f(v)`. 可以验证它满足自然变换的交换图表: `V overset (theta_V) to V^(ast ast)`
    `A darr qquad darr A^(ast ast)`
    `W underset (theta_W) to W^(ast ast)`     其中 `theta_W @ A = A^(ast ast) @ theta_V`. 同理有另一个自然变换 `"id"_(sf(V ect)(bbb F)^"op") to D^"op" D`. 当线性空间限制到有限维时, 这两个自然变换都是自然同构.

如图: `U overset B to V overset A to W`,
`U^ast overset (B^ast) larr V^ast overset (A^ast) larr W^ast`. 先熟悉星号运算: 1. `v_1^(ast ast) v_2^ast = v_2^ast v_1`;
2. `quad A^ast w^ast = w^ast A`;
3. `quad (A B)^ast = B^ast A^ast`;
4. `quad (A v)^(ast ast) = A^(ast ast) v^(ast ast)`. 前两式由定义即可获得. 3. 的证明: `(A B)^ast w^ast` `= w^ast (A B)` `= (w^ast A) B` `= (A^ast w^ast) B` `= B^ast(A^ast w^ast)` `= (B^ast A^ast) w^ast`. 4. 的证明: `(A v)^(ast ast) w^ast` `= w^ast (A v)` `= (w^ast A) v` `= v^(ast ast) (w^ast A)` `= v^(ast ast) (A^ast w^ast)` `= (v^(ast ast) A^ast) w^ast` `= (A^(ast ast) v^(ast ast)) w^ast`. 事实上, 性质 4 说明 `theta` 正是一个自然同态.

一般而言, 两个有限维线性空间只要维数相同, 都是同构的, 但这个同构依赖于基的选取. 但 `V` 到 `V^(ast ast)` 的同构 `v mapsto f mapsto f(v)` 不依赖于基的选择, 因此说它是自然的.

双重对偶空间可以推广到模范畴上. 事实上, 设 `R` 为一环, 用 `sf(R)"-"sf(Mod), sf(Mod)"-"sf(R)` 分别表示左右 `R`-模范畴, 可以给出反变函子: `D: sf(R)"-"sf(Mod) to sf(Mod)"-"sf(R)`
(对象层次) `M mapsto M^ast`,
(态射层次) `A mapsto A^ast`. 其中 `M^ast` 表示全体模同态 `M to R` 构成的右 `R`-模. 模同态 `A: M to N` 在函子 `D` 的作用下变成对偶同态 `A^ast: N^ast to M^ast`. 类似可以定义 `D^"op"` 和自然同态 `theta: "id" to D D^"op"`.
模论的一些术语: 若态射 `theta_M: M to M^(ast ast)` 是单的, 则称 `M` 是无挠的 (torsionfree) 或半自反的 (semi-reflexive); 若 `theta_M` 是同构, 则称 `M` 是自反的 (reflexive).

范畴同构与等价

    设 `cc C, cc D` 为范畴,
  1. 若存在函子 `F: cc C to cc D` 和 `G: cc D to cc C`, 使得 `G F = "id"_(cc C)`, `quad F G = "id"_(cc D)`, 则称 `cc C` 与 `cc D` 同构.
  2. 把上面条件中的等号 "`=`" 减弱为自然同构 "`~=`", 则称 `cc C` 与 `cc D` 等价, 并简记 `(F, G)` 是一个等价.
  1. Abel 群范畴与 `ZZ`-模范畴同构;
  2. 左 `R`-模范畴 `sf(R)"-"sf(Mod)` 与右 `R`-模范畴的反范畴 `sf(Mod)"-"sf(R)^"op"` 同构;

范畴等价的判定 给定函子 `F: cc C to cc D`, 则存在函子 `G: cc D to cc C` 使得 `(F, G)` 是一个等价的充要条件是 `F` 是全忠实且本质满函子.

  1. `rArr`: 设 `(F, G)` 是一个等价, 即 `F G ~= "id"_(cc D)`, `G F ~= "id"_(cc C)`.
    1. `F` 本质满: `AA A: cc D`, 由于 `F G ~= "id"_(cc D)` 有 `F G(A) ~= A`, 这指出 `A` 与 `G(A)` 在 `F` 下的像只相差一个同构.
    2. `F` 忠实: 由于 `G F ~= "id"_(cc C)`, 有交换图 `A overset (eta_A) to G F(A)`
      `f darr qquad darr G F(f)`
      `B underset (eta_B) to G F(B)`       其中 `eta_A`, `eta_B` 皆为同构. 从而 `G F(f) = eta_B f eta_A^-1` 是双射. 于是 `AA f, g: A to B`, `F(f) = F(g)` `rArr G F(f) = G F(g)` `rArr f = g`, 故 `F` 忠实, 同理 `G` 也是忠实的.
    3. `F` 完全: 对 `AA g: F(A) to F(B)`, `G(g): G F(A) to G F(B)`. 由于 `G F` 是双射, 存在 `f: A to B` 使得 `G(g) = G F(f)`, 而 `G` 忠实故 `g = F(f)`.
  2. `lArr`: 由 `F` 本质满, `AA A: cc D`, `EE A': cc C` 使得 `A ~= F(A')`, 记它们之间的同构为 `eta_A`. 定义函子 `G: cc D to cc C`,
    `G(A) := A'`.     如果对任意 `f: A to B` 成立 `F G(f) = eta_B f eta_A^-1`, 则成立交换图 `A overset (eta_A) to F G(A)`
    `f darr qquad darr F G(f)`
    `B underset (eta_B) to F G(B)`     这是可以做到的: 由于 `F` 完全忠实, 存在唯一 `f': A' to B'` 使得 `F(f') = eta_B f eta_A^-1`. 于是取 `G(f) := f'` 即可. 由交换图知道 `F G ~= "id"_(cc D)`.
    再证 `G F ~= "id"_(cc C)`. 任取 `A, B: cc C`, `f: A to B`, 将上图的 `A, B, f` 分别换成 `F(A), F(B), F(f)`, 则成立交换图 `F(A) overset (eta_(F(A))) to F G F(A)`
    `F(f) darr qquad darr F G F(f)`
    `F(B) underset (eta_(F(B))) to F G F(B)`     因为 `eta_(F(A))` 是同构, `F` 是全忠实函子, 所以存在唯一同构 `xi_A: A to G F(A)` 使得 `F(xi_A) = eta_(F(A))`. 同理存在唯一同构 `xi_B: B to G F(B)` 使得 `F(xi_B) = eta_(F(B))`. 将上图的 `eta_(F(A))`, `eta_(F(B))` 改写为 `F(xi_A)`, `F(xi_B)`, 然后整张图左侧脱去函子 `F` (因为 `F` 忠实): `A overset (xi_A) to G F(A)`
    `f darr qquad darr G F(f)`
    `B underset (xi_B) to G F(B)`     这证明了 `G F ~= "id"_(cc C)`.

泛性质

范畴论中, 常常通过对象在交换图表中的性质 (泛性质) 来定义它们. 这些对象如果存在则必唯一 (精确到同构).

始对象与终对象

  1. 始对象 若 `X: cc C` 满足: 对任意 `Y: cc C` 都存在唯一态射 `f: X to Y`, 则称 `X` 是 `cc C` 的始对象 (initial object).
  2. 终对象 若 `X: cc C` 满足: 对任意 `Y: cc C` 都存在唯一态射 `f: Y to X`, 则称 `X` 是 `cc C` 的终对象 (final object).
    3. 始对象与终对象互为对偶. 如果始对象与终对象同构, 则称它为 `cc C` 的零对象, 记为 `0`.
  1. `sf(Set)` 中, 始对象是空集, 终对象是单元素集合 (所有单元素集合同构);
  2. `sf(Grp)` 中, 平凡群是零对象; `sf(Mod)_R` 中, 零模是零对象;
  3. `sf(Rng)` 中, 零环是零对象. `sf(Ri ng)` 中, 始对象是 `ZZ`, 终对象是零环. 如果要求环的 `0 != 1`, 则 `sf(Ri ng)` 没有终对象.
  4. 域范畴既没有始对象也没有终对象.
  5. 偏序范畴 `(ZZ^+, le)` 中, `1` 是始对象, 没有终对象.

积与余积

  1. 积 对 `X, Y: cc C`, 若存在对象 `W: cc C` 和态射 `pi_1: W to X`, `pi_2: W to Y` 满足下列条件, 则称 `W` 是 `X` 和 `Y` 的积 (product), 并记 `W = X xx Y`:
    对任意 `Z: cc C` 和态射 `f: Z to X`, `g: Z to Y`, 都有唯一的态射 `u: Z to W` 使下图交换:
    积
    `pi_1, pi_2` 称为投影映射, `u` 一般记为 `(f, g)`.
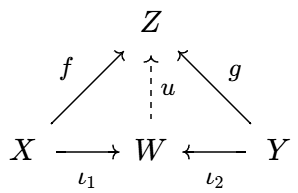
  2. 余积 对 `X, Y: cc C`, 若存在对象 `W: cc C` 和态射 `iota_1: X to W`, `iota_2: Y to W` 满足下列条件, 则称 `W` 是 `X` 和 `Y` 的余积 (coproduct), 并记 `W = X ⊔ Y`:
    对任意 `Z: cc C` 和态射 `f: X to Z`, `g: Y to Z`, 都有唯一的态射 `u: W to Z` 使下图交换:
    余积
    `iota_1, iota_2` 称为包含映射, `u` 一般记为 `f o+ g` 或 `f ⊔ g`.
  1. `sf(Set)` 中, 积就是集合的笛卡尔积, 余积是集合的无交并: `A ⊔ B := {(a, x): x in A} uu {(b, y): y in B}`;
  2. `sf(Mod)_R` 中, 积是模的积, 余积是模的直和: 直积: `prod M_i = { x = sum x_i: x_i in M_i }`
    直和: `o+ M_i := { x = 有限和 sum x_i: x_i in M_i }`.
  3. `sf(Ri ng)` 中, 积是环的积, 余积也存在, 但较为复杂;
  4. 考虑偏序范畴 `(RR, le)`. 对一族实数 `S sube RR`, 它们的积和余积分别是 `inf S` 和 `Sup S`. 当然, 只有当 `S` 有界时, 积和余积才同时存在.

等化子与余等化子

生成子 若存在对象 `U in cc C`, 使得对于任意两个对象 `X, Y in cc C`, 和两个不同态射 `f != g: X to Y`, 都存在 `u: U to X` 使得 `f @ u != g @ u`, 则称 `U` 是 `cc C` 的生成子.

群范畴 `sf(Grp)` 的生成子是 `ZZ`.

生成子的效果是, 使得原先不同的两个态射, 在复合一个态射之后仍是不同的. 等化子则相反, 它使两个态射在复合一个态射之后变得相同.

    令 `X, Y: cc C`, `f, g: X to Y`.
  1. 等化子 (equalizer) 若存在对象 `E` 和态射 `e: E to X`, 使得 `f @ e = g @ e`, 且态射 `e` 在相差一个态射的意义下唯一, 则称 `E` 是 `X, Y` 的等化子. 这里的“相差一个态射”是指: 对任意对象 `E': cc C`, 若存在 `e': E' to X` 使得 `f @ e' = g @ e'`, 则存在唯一态射 `u: E' to E` 使得 `e' = e @ u`.
  2. 余等化子 (coequalizer) 若存在对象 `Q` 和态射 `q: Y to Q`, 使得 `q @ f = q @ g`, 且态射 `q` 在相差一个态射的意义下唯一, 则称 `Q` 是 `X, Y` 的余等化子.

这里的字母 `E, Q` 取自 equalizer 的前两个字母.

  1. 在数学中 "某某化子" 是指使某性质局部成立的对象的集合. 例如两个函数 `f, g: X to Y` 的等化子就是集合 `{x in X: f(x) = g(x)}`.
  2. `sf(Set)` 中, 两个态射 `f, g: X to Y` 的等化子是 `{x in X: f(x) = g(x)}`.
  3. `sf(Mod)_R` 中, 态射 `f, g: M to N` 的等化子是 `"Ker"(f - g)`, 余等化子是 `N//"Im"(f - g)`.