勾股定理

直角三角形的两直角边长为 `a, b`, 则斜边 `c` 满足 `c^2 = a^2 + b^2` (勾股定理). 斜边上的高 `h` 满足 `1/h^2 = 1/a^2 + 1/b^2` (倒数勾股定理).

应用面积法知道 `c h = a b`, 于是 `1/h^2 = (c/(a b))^2 = (a^2 + b^2)/(a^2 b^2) = 1/a^2 + 1/b^2`.

正弦/余弦定理

正弦定理

由面积关系 `2S = b c sin A = a c sin B`, 得到: `(sin A)/a = (sin B)/b`. 此外有圆周角和其所对弦长的关系 `a = 2 R sin A`.

三角形的面积

Heron 公式 设三角形的三边长分别为 `a, b, c`, 其周长的一半为 `p = (a+b+c)//2`, 则三角形的面积为 `S = sqrt(p(p-a)(p-b)(p-c))`.

记边 `a, b` 的夹角为 `C`, 利用余弦定理 `cos C = (a^2+b^2-c^2)/(2a b)`, 有 `16S^2 = 16 (1/2 a b sin C)^2` `= (2a b)^2 (1-cos^2 C)` `= (2a b)^2 (1+(a^2+b^2-c^2)/(2a b)) (1-(a^2+b^2-c^2)/(2a b))` `= [(a+b)^2-c^2][c^2-(a-b)^2]` `= (a+b+c)(a+b-c)(c+a-b)(c-a+b)`, 结论得证.

三维欧氏空间中, `cos AOC = alpha`, `cos BOC = beta`, `cos AOB = gamma`. 求 `OC` 与平面 `AOB` 的夹角余弦值 `rho`.

不妨设 `OC = 1`, 作 `CH` 垂直平面 `AOB` 于 `H`, 则 `OH = rho`, `cos AOH = alpha//rho`, `cos BOH = beta//rho`, 于是 `gamma = cos AOB` `= cos(AOH +- BOH)` `= (alpha beta -+ sqrt((rho^2-alpha^2)(rho^2-beta^2)))/rho^2`. `OC` 不垂直于平面 `AOB` 时, 解得 `rho^2 = (alpha^2 + beta^2 - 2alpha beta gamma)/(1-gamma^2)`. 显然上式也适用于 `OC` 垂直于平面 `AOB` 的情形.

Euler 四面体问题 已知四面体六棱长, 求体积.

记这个四面体为 `OABC`, 其中 `OA = a`, `OB = b`, `OC = c`, `AB = p`, `AC = q`, `BC = r`. 利用余弦定理, `gamma := cos AOB = (a^2+b^2-p^2)/(2a b)`,
`alpha := cos AOC = (a^2+c^2-q^2)/(2a c)`,
`beta := cos BOC = (b^2+c^2-r^2)/(2b c)`. 利用引理有 `V^2 = (1/3 S_(AOB) h)^2` `= (1/6 a b sin AOB h)^2` `= (1/6 a b c)^2 (1-gamma^2) (1-alpha^2-beta^2-gamma^2 + 2alpha beta gamma)/(1-gamma^2)`. 即 `((6V)/(a b c))^2 = 1-alpha^2-beta^2-gamma^2 + 2alpha beta gamma`.

记号同前一种解法. 又记 `vec(OA) := bm a = (a_1, a_2, a_3)`, `vec(OB) := bm b = (b_1, b_2, b_3)`, `vec(OC) := bm c = (c_1, c_2, c_3)`, 则 `36 V^2 = |a_1, a_2, a_3; b_1, b_2, b_3; c_1, c_2, c_3| |a_1, b_1, c_1; a_2, b_2, c_2; a_3, b_3, c_3|` `= | bm a * bm a, bm a * bm b, bm a * bm c; bm b * bm a, bm b * bm b, bm b * bm c; bm c * bm a, bm c * bm b, bm c * bm c |` `= | a^2, gamma a b, alpha a c; gamma a b, b^2, beta b c; alpha a c, beta b c, c^2 |` `= (a b c)^2 | 1, gamma, alpha; gamma, 1, beta; alpha, beta, 1 |` `= (a b c)^2 (1-alpha^2-beta^2-gamma^2 + 2 alpha beta gamma)`. 结果与前相同.

设有矩形 `ABCD`, `E, F` 分别在边 `BC, CD` 上, `S_(ABE) = x`, `S_(ADF) = y`, `S_(CEF) = z`. 求 `S_(AEF)`.

设 `AB = a`, `AD = b`, 则 `BE = (2x)/a`, `DF = (2y)/b`. 利用 `S_(CEF)` 列出方程: `(b-(2x)/a)(a-(2y)/b) = 2 z`, 即 `(a b-2x)(a b-2y) = 2 a b z`. 上式视为 `a b` 的方程, 解得 `a b = x+y+z +- sqrt((x+y+z)^2-4x y)`. 显然 `a b gt x + y + z`, 上式应取正号, 所以 `S_(AEF) = sqrt((x+y+z)^2-4x y)`.

定比分点, 齐次坐标与三角形的心

定比分点

设 `AB` 是线段, `lambda, mu, k` 为实数, 若点 `P` 满足 `vec(AP) = k lambda vec(AB)`, `quad vec(PB) = k mu vec(AB)`. 则称 `P` 把 `AB` 分成了 `lambda//mu`. 特别当 `P` 在线段 `AB` 上时, 称 `P` 是 `AB` 的内分点.

定比分点公式 设 `O` 是平面上任一点, `AB` 是一线段. 则平面上一点 `P` 把 `AB` 分成 `lambda//mu`, `lambda+mu=1` 当且仅当 `vec(OP) = mu vec(OA) + lambda vec(OB)`. 特别 `lambda = mu = 1/2` 刻画了 `P` 是 `AB` 中点的情形: `vec(OP) = 1/2 (vec(OA) + vec(OB))`.

在 `triangle ABC` 中, 分别用 `a, b, c` 记三个角 `A, B, C` 的对边, 点 `P` 满足 `vec(AP) = lambda vec(PB)`. 则
1. `P` 是 `AB` 中点时, `lambda = 1`;
2. (角平分线定理) `CP` 是 `/_ACB` 的平分线时, `lambda = S_(ACP)/S_(BCP) = b/a = (sin B)/(sin A)`;
3. `CP` 是 `AB` 边上的高时, `lambda = (b cos A)/(a cos B) = (sin B cos A)/(sin A cos B)` `= (tan B)/(tan A)`.

Stewart 定理 设有 `triangle ABC`, 内分点 `P` 将 `AB` 分成了 `lambda//mu`, `lambda+mu=1`. 分别用 `a, b, c` 记 `triangle ABC` 中 `A, B, C` 的对边, 则 `|CP|^2 = lambda a^2 + mu b^2 - lambda mu c^2`.

由定比分点公式 `vec(CP) = mu vec(CA) + lambda vec(CB)`, 由余弦定理 `cos /_ACB = (a^2+b^2-c^2)/(2a b)`. 于是 `|vec(CP)|^2` `= mu^2 |vec(CA)|^2 + lambda^2 |vec(CB)|^2 + 2 lambda mu vec(CA) * vec(CB)`
`= lambda^2 a^2 + mu^2 b^2 + 2lambda mu a b cos/_ACB`
`= lambda^2 a^2 + mu^2 b^2 + lambda mu (a^2+b^2-c^2)`
`= lambda a^2 + mu b^2 - lambda mu c^2`.

中线长与角平分线长 设 `triangle ABC` 中, `a, b, c` 分别是 `A, B, C` 的对边, `p = (a+b+c)//2`, 边 `c` 上的中线长与角平分线长分别记为 `m_c`, `t_c`. 由 Stewart 定理和得到
1. `4 m_c^2 = 2(a^2+b^2)-c^2`;
2. `t_c^2 = ((2a b)/(a+b)cos{:C/2:})^2` `= (2/(a+b))^2 a b p(p-c)` `= a b - (a c)/(a+b) (b c)/(a+b)`. 设角平分线与 `AB` 交于 `P`, 最后一个公式即为 `|CP|^2 = |CA| |CB| - |AP| |PB|`.
3. `4(m_c^2-t_c^2)` `= (2(a^2+b^2) - 4a b) + ((4a b c^2)/(a+b)^2 - c^2)` `= 2(a-b)^2 - c^2/(a+b)^2 (a-b)^2` `= ((a-b)/(a+b))^2 [2(a+b)^2-c^2]`. 可见中线总是长于或等于角平分线. 二者相等当且仅当 `a = b`.

齐次坐标

设平面上有一点 `X` 和 `triangle ABC`, 如果存在实数 `x_A, x_B, x_C` 满足 `x_A + x_B + x_C = 1`, 且 `x_A vec(AX) + x_B vec(BX) + x_C vec(CX) = bb 0`. 则称 `(x_A, x_B, x_C)` 为 `X` 关于 `triangle ABC` 的齐次坐标.

`X` 关于 `triangle ABC` 的齐次坐标存在唯一.

存在性: 平面上三个向量必线性相关, 故存在不全为零的实数 `k_1, k_2, k_3` (不妨设 `k_3 != 0`) 使得 `k_1 vec(AX) + k_2 vec(BX) + k_3 vec(CX) = bb 0`. 假设 `k_1 + k_2 + k_3 = 0`, 则在等式 `k_1 vec(AX) + k_2 vec(BX) = -k_3 vec(CX)` 两边同除以 `-k_3` 得 `k_1/(k_1+k_2) vec(AX) + k_2/(k_1+k_2) vec(BX) = vec(CX)`. 由定比分点公式知 `A, B, C` 共线, 这与 `A, B, C` 三点构成一个三角形矛盾, 所以 `k_1 + k_2 + k_3 != 0`. 记 `x_i = k_i//(k_1+k_2+k_3)`, `i = 1, 2, 3`, 则 `(x_1, x_2, x_3)` 就是 `X` 关于 `triangle ABC` 的齐次坐标.
唯一性: 设 `(x_1, x_2, x_3)` 和 `(y_1, y_2, y_3)` 都是 `X` 关于 `triangle ABC` 的齐次坐标, 我们有 `x_1 vec(AX) + x_2 vec(BX) + x_3 vec(CX) = bb 0`,
`y_1 vec(AX) + y_2 vec(BX) + y_3 vec(CX) = bb 0`. 相减得 `(x_1-y_1)vec(AX) + (x_2-y_2)vec(BX) + (x_3-y_3)vec(CX) = bb 0`. 假设 `(x_1, x_2, x_3) != (y_1, y_2, y_3)`, 则 `x_1-y_1, x_2-y_2, x_3-y_3` 不全为零. 由存在性部分的证明知, 此时 `(x_1-y_1) + (x_2-y_2) + (x_3-y_3) != 0`. 与 `x_1+x_2+x_3 = y_1+y_2+y_3 = 1` 矛盾. 故 `(x_1, x_2, x_3) = (y_1, y_2, y_3)`.

`(x_A, x_B, x_C)` 是 `X` 关于 `triangle ABC` 的齐次坐标, 当且仅当对平面上的任意一点 `O` 有 `vec(OX) = x_A vec(OA) + x_B vec(OB) + x_C vec(OC)`. 这一结论帮助我们将齐次坐标化为普通坐标.

充分性: 将点 `A, B, C` 分别代入 有 `vec(AX) = x_B vec(AB) + x_C vec(AC)`,
`vec(BX) = x_A vec(BA) + x_C vec(BC)`,
`vec(CX) = x_A vec(CA) + x_B vec(CB)`. 所以 成立.
必要性: 易知 `x_A, x_B, x_C` 不全为零, 不妨设 `x_A != 0`, 有 `{: vec(OX) ,= vec(OA) + vec(AX); ,= vec(OA) - 1/x_A (x_B vec(BX) + x_C vec(CX)); ,= vec(OA) - 1/x_A [x_B (vec(OX)-vec(OB)) + x_C(vec(OX)-vec(OC))]; ,= vec(OA) + x_B/x_A vec(OB) + x_C/x_A vec(OC) - (x_B+x_C)/x_A vec(OX). :}` 利用 `x_A + x_B + x_C = 1`, 整理即得式 .

下面推导齐次坐标的计算公式, 为此先引入三角形的有向面积的概念:

1. 三角形的有向面积的绝对值等于三角形的面积;
2. 当三个顶点的书写次序为逆时针时, 三角形的有向面积的符号为正, 否则为负.

设平面上有一点 `X` 和 `triangle ABC`, 三角形 `ABC, BCX, CAX, ABX` 的有向面积分别记为 `S, S_A, S_B, S_C`. 则点 `X` 关于 `triangle ABC` 的齐次坐标是 `1/S(S_A, S_B, S_C)`.

(更具一般性的证明? 交点 `P` 的存在性?) 任取平面上一点 `O`. 设直线 `CX` 交 `AB` 于 `P`, 注意到 `AP//BP = S_B//S_A`, 有 `vec(OP) = 1/(S_A + S_B) (S_A vec(OA) + S_B vec(OB))`. 另外, 容易得到 `S_(APM) = S_C S_B/(S_A + S_B)`, 故知 `(CM)/(MP) = S_B/S_(APM) = (S_A + S_B)/S_C`. 从而 `vec(OM) = 1/(S_A+S_B+S_C)[(S_A+S_B) vec(OP) + S_C vec(OC)]` `= 1/S (S_A vec(OA) + S_B vec(OB) + S_C vec(OC))`.

Menelaus 定理与 Ceva 定理

设有 `triangle ABC`, `P, Q, R` 分别在直线 `AB, BC, CA` 上, 满足 `vec(AP) = lambda vec(PB)`, `vec(BQ) = mu vec(QC)`, `vec(CR) = nu vec(RA)`, 则
1. Menelaus 定理 `P, Q, R` 共线当且仅当 `lambda mu nu = -1`;
2. Ceva 定理 若 `P, Q, R` 都是内分点, 则 `AQ, BR, CP` 共点当且仅当 `lambda mu nu = 1`.

1. 容易写出 `vec(A P) = lambda/(1+lambda) vec(A B)`, `quad vec(A Q) = 1/(1+mu) vec(A B) + mu/(1+mu) vec(A C)`, `quad vec(A R) = 1/(1+nu) vec(A C)`. 三点 `P, Q, R` 共线当且仅当它们围成的三角形面积为零, 即 `0 = | lambda/(1+lambda), 0, 1; 1/(1+mu), mu/(1+mu), 1; 0, 1/(1+nu), 1; |` `iff` `0 = | lambda,0,1+lambda; 1,mu,1+mu; 0,1,1+nu; |` `= | lambda,0,1; 1,mu,0; 0,1,nu; |` `= lambda mu nu + 1`.
2. 设三线交于点 `M`, 利用等式 ` lambda mu nu = (AP * BQ * CR)/(BP * CQ * AR) = (S_(AMC) * S_(BMA) * S_(CMB)) / (S_(BMC) * S_(CMA) * S_(AMB)) = 1` 立即得到必要性. 为证充分性, 设 `AQ`, `BR` 交于 `M`, 容易看出, 上式成立当且仅当 `M` 在 `CP` 上, 即三线共点.

各字母假定同上. `AQ, BR, CP` 叫 Ceva 线, `triangle PQR` 叫 Ceva 三角形.

角元 Ceva 定理 设 `P, Q, R` 分别是 `triangle ABC` 三边 `AB, BC, CA` 的内分点, 六个角 `/_ ACP`, `/_ PCB`, `/_ BAQ`, `/_ QAC`, `/_ CBR`, `/_ RBA` 依次记为 `/_ 1` 到 `/_ 6`, 则 `AQ, BR, CP` 共点当且仅当 `sin /_1 sin /_3 sin /_5 = sin /_2 sin /_4 sin /_6`.

必要性: 设三线共点于 `M`. 由正弦定理 `(sin /_1)/(AM) = (sin /_4)/(CM)`, `quad (sin /_5)/(CM) = (sin /_2)/(BM)`, `quad (sin /_3)/(BM) = (sin /_6)/(AM)`. 三式相乘即得结论. 充分性的证明与 Ceva 定理类似.

设圆周上顺次有 `A, B, C, D, E, F` 六点, 则 `AD, BE, CF` 共点当且仅当 `AB * CD * EF = BC * DE * FA`.

在 `triangle ACE` 中应用角元 Ceva 定理, 注意到圆周角所对的弦长正比于该圆周角的正弦值 (事实上有 `a = 2 R sin theta`, `a` 为弦长, `R` 为半径, `theta` 为圆周角), 即得结论.

角格点问题 三角形 `ABC` 内有一点 `O`, 若已知六个角 `OAB`, `OAC`, `OBA`, `OBC`, `OCA`, `OCB` 中的四个, 则可以用角元 Ceva 公式求出另外两个. 特别当六个角的度数都是有理数时, 称 `O` 为三角形的角格点. 如 `sin 10^@ * sin 20^@ * sin 70^@ = sin 10^@ * sin 30^@ * sin 40^@`. 上式简记为 1 2 7 1 3 4. 用程序穷举所有 10 度的倍数的角格点如下:

三角形的心

假设如 Ceva 定理. 设 `AQ, BR, CP` 相交于点 `X`, 则 `X` 关于 `triangle ABC` 的齐次坐标是 `(1/(1+lambda+lambda mu), 1/(1+mu+mu nu), 1/(1+nu+nu lambda))`.

`S_A, S_B, S_C` 的定义见. 将 `S_B//S_A = lambda`, `quad S_C//S_B = mu`, `quad S_A//S_C = nu` 代入 `S_A + S_B + S_C = S` 得到 `S_A(1 + lambda + lambda mu) = S`,
`S_B(1 + mu + mu nu) = S`,
`S_C(1 + nu + nu lambda) = S`. 再由即得结论.

三角形的五心 三角形的
1. 三条中线交于一点, 称为重心;
2. 三条角平分线交于一点, 称为内心; 内心是三角形内切圆的心;
3. 三条高所在的直线交于一点, 称为垂心;
4. 三边的中垂线交于一点, 称为外心; 外心是三角形外接圆的心;
5. 任一内角平分线与另外两个外角平分线交于一点, 称为旁心; 旁心共有三个，分别是三角形三个外切圆的心;
6. 三个顶点到对边上旁切圆切点的连线交于一点, 称为界心.

• 由 Ceva 定理和 立即得到重心, 内心和垂心的存在性.
• 证明旁心存在性, 利用如下命题: 设 `l` 是过角的顶点的直线, 则以下三款等价:
  1. `l` 平分角;
  2. `l` 上任意一点到角两边的距离相等;
  3. `l` 上存在一点到角两边的距离相等.
  容易证明, 若三角形的两条角平分线交于一点, 则这点与第三点的连线是第三条角平分线.
  这一命题也可用于证明内心的存在性.
• 证明外心存在性, 可利用如下命题: 设 `l` 是过线段中点的直线, 则以下三款等价:
  1. `l` 垂直于线段;
  2. `l` 上任意一点到线段两端的距离相等;
  3. `l` 上存在一点到线段两端的距离相等.
  容易证明, 若三角形两边的中垂线交于一点, 则这点与第三边中点的连线是第三条中垂线.
• 垂心存在性的又一证明: 设 `triangle ABC` 的两条高线 `AQ, BR` 交于点 `H`, 下证 `HC _|_ AB`. 事实上, `HC _|_ AB` `iff vec(HC) * vec(AB) = 0` `iff vec(HC) * (vec(HB) - vec(HA)) = 0` `iff vec(HC) * vec(HA) = vec(HC) * vec(HB)`, 同理, `HA _|_ BC`, `HB _|_ CA` 等价于 `vec(HA)*vec(HB) = vec(HA)*vec(HC)`,
  `vec(HB)*vec(HC) = vec(HB)*vec(HA)`. 于是 `vec(HC) * vec(HA) = vec(HC) * vec(HB)`, 即 `HC _|_ AB`. 由以上证明知, 垂心 `H` 满足等式 `vec(HA) * vec(HB) = vec(HB) * vec(HC) = vec(HC) * vec(HA)`.

重心与内心都在三角形的内部; 三个旁心都在三角形的外部; 外心和垂心则不一定.

利用和 容易算出 `triangle ABC` 各心的齐次坐标:
1. 重心 `G`: `(1, 1, 1)`;
2. 内心 `I`: `(a, b, c) = (sin A, sin B, sin C)`;
3. 垂心 `H`: `(tan A, tan B, tan C)`, 如果 `A` 为直角, 此时 `tan A = oo`, 坐标视为 `(1, 0, 0)`;
4. 外心 `O`: `(sin 2A, sin 2B, sin 2C)`;
5. 旁心 `J_A`: `(-a, b, c)`. 其中 `J_A` 与 `A` 在直线 `BC` 异侧; `J_B`, `J_C` 的坐标可以轮换得到.
6. 界心 `N`: `(p-a, p-b, p-c)` `= (cot{:A/2:}, cot{:B/2:}, cot{:C/2:})`, 其中 `p = (a+b+c)//2`.

1. 外心的 `lambda` 值的计算思路是: `lambda = S_(AOC)/S_(COB) = (sin /_AOC)/(sin /_COB)` `= (sin 2B)/(sin 2A)`.
2. 旁心的 `lambda` 值的计算思路是 (用 `sigma` 表示有向面积): `lambda = sigma_(A J_A C)/sigma_(C J_A B)` `= - (b sin{:(pi-C)/2:})/(a sin{:(pi-C)/2:})` `= -b/a`, 以及 `mu = c//b`, `nu = -a//b`.
3. 界心的 `lambda = (p-b)/(p-a)`.

设 `A + B + C = pi`, 则有 `sin A + sin B + sin C = 4 cos{:A/2:}cos{:B/2:}cos{:C/2:}`,
`tan A + tan B + tan C = tan A tan B tan C`,
`sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C`. 参见三角形中的恒等式.

设 `triangle ABC` 的面积为 `S`, `p = (a+b+c)//2`, 则内切圆 `I`, 旁切圆 `J_A, J_B, J_C` 的半径分别是 `r = S/p`, `quad r_A = S/(p-a)`, `quad r_B = S/(p-b)`, `quad r_C = S/(p-c)`. 由三角形面积的 Heron 公式推知, `S^2 = r r_A r_B r_C`.

注意到 `S` 是 `triangle BCI`, `triangle CAI`, `triangle ABI` 的面积之和: `S = 1/2 a r + 1/2 b r + 1/2 c r`, 即得到 `r = S//p`.
再由 `S` 是 `triangle BCJ_A`, `triangle CAJ_A`, `triangle ABJ_A` 的有向面积之和: `S = -1/2 a r_A + 1/2 b r_A + 1/2 c r_A`, 即得到 `r_A = S//(p-a)`

余切定理 `triangle ABC` 中, 记 `p = (a+b+c)//2`, `r` 为内切圆半径, 则 `cot{:A/2:} = (p-a)/r`, `quad cot{:B/2:} = (p-b)/r`, `quad cot{:C/2:} = (p-c)/r`. 结合内, 外切圆的半径长度, 有: 三角形每个外切圆到其对面顶点 (如, 圆 `J_A` 到点 `A`) 的切线长都等于 `p`.

设内切圆 `I` 在边 `AB, BC, CA` 上的切点分别为 `P, Q, R`. 设 `AP = AR = x`, `BP = BQ = y`, `CQ = CR = z`, 于是 `y+z = a`, `quad z+x = b`, `quad x+y = c`. 解得 `x = p-a`, `y = p-b`, `z = p-c`. 在 `triangle API` 中可以验证 `cot{:A/2:}`. 其余类似.

三角形的三个旁心相连接形成的三角形称为它的旁心三角形. 三角形的三个垂足相连接形成的三角形称为它的垂足三角形. 如果 `ABC` 是 `DEF` 的旁心三角形, 则 `DEF` 是 `ABC` 的垂足三角形, 反之亦然. 垂足三角形是周长最小的内接三角形.

重心是平面上到三角形三个顶点距离平方和最小的点, 也是三角形内部到三边距离之积最大的点.

1. 设三个顶点的坐标分别为 `(x_i, y_i)`, `i = 1,2,3`. 则点 `(x,y)` 到它们距离的平方和为 `f(x,y) = sum_(i=1)^3 ((x-x_i)^2+(y-y_i)^2)`. 求导有 `(del f)/(del x) = 2 sum_(i=1)^3 (x-x_i)`, `quad (del f)/(del y) = 2 sum_(i=1)^3 (y-y_i)`,
   Hessian 矩阵 `[(del^2 f)/(del x^2), (del^2 f)/(del x del y); (del^2 f)/(del y del x), (del^2 f)/(del y^2)]` `= 6 [1, 0; 0, 1]` 正定. 令 `(del f)/(del x) = (del f)/(del y) = 0` 求得极小值点 `(x,y) = 1/3(x_1+x_2+x_3,y_1+y_2+y_3)`. 这是三角形的重心.
2. 设点 `X` 的齐次坐标是 `1/S(S_A, S_B, S_C)`, 则它到三边距离之积等于 `(2S_A)/a (2S_B)/b (2S_C)/c` `le 8/(a b c) ((S_A + S_B + S_C)/3)^3` `= 8/27 S^3/(a b c)`. 等号成立当且仅当 `S_A = S_B = S_C`, 即 `X` 是三角形的重心.

鸡爪定理 [来自 百度百科] 在 `triangle ABC` 中, `/_ C` 的平分线与外接圆交于 `K`, 设内心为 `I`, `/_ C` 所对的旁心为 `J`, 则 `A, B, I, J` 四点共圆, 圆心为 `K`. 此时线段 `KA`, `KB`, `KI`, `KJ` 形似鸡爪, 故称为鸡爪定理.

1. `KA = KB`: 相等圆周角所对的弦相等.
2. `KA = KI`: 只需证 `/_ KAI = /_ KIA`, 即证 `/_ KAB + /_ BAI = /_ KCA + /_ IAC`. 上式成立, 这是因为 `/_ KAB = /_ KCB = /_ KCA`, `quad /_ BAI = /_ IAC`.
3. 由 1, 2 知道 `K` 是 `ABI` 的外心, 下证 `A, B, I, J` 四点共圆. 事实上由 `AI`, `AJ` 分别是三角形内角与外角的平分线知道, `/_ IAJ` 是直角. 同理 `/_ IBJ` 也是直角, 这就推出 `A, B, I, J` 四点共圆.

设 `A, B, C` 三点到原点 `O` 的距离分别为 `a, b, c`, 求三角形 `ABC` 面积的最大值.

首先说明, 只有 `O, A, B, C` 四点共面时, 三角形面积才能取得最大值. 若三角形面积最大时四点不共面, 可设 `O` 在平面 `ABC` 上的投影为 `O'`, 有 `O'A lt OA`, `O'B lt OB`, `O'C lt OC`. 但如果延长 `O'A`, `O'B`, `O'C` 三条线段, 使它们分别等于 `OA`, `OB`, `OC`, 所得的三角形面积将更大, 矛盾.
下面假设四点共面. 记 `vec(OA) = bm a`, `vec(OB) = bm b`, `vec(OC) = bm c`, `(:bm a, bm b:) = theta_1`, `(:bm b, bm c:) = theta_2`, `(:bm c, bm a:) = theta_3`, 则三角形面积的两倍等于 `a b sin theta_1 + b c sin theta_2 + c a sin theta_3`. 设 `f = a b sin theta_1 + b c sin theta_2 + c a sin theta_3 - lambda(theta_1 + theta_2 + theta_3 - 2pi)`. 于是 `(del f)/(del theta_1) = a b cos theta_1 - lambda`, `quad (del f)/(del theta_2) = b c cos theta_2 - lambda`, `quad (del f)/(del theta_3) = c a cos theta_3 - lambda`. 令三个偏导数为零知, 当 `bm a * bm b = bm b * bm c = bm c * bm a = lambda` 时, 三角形面积最大 (此时原点是三角形的垂心). 将 `a b cos theta_1 = b c cos theta_2 = c a cos theta_3` 中的 `cos theta_2, cos theta_3` 用 `cos theta_1` 表示, 再代入 `cos theta_3 = cos(2pi-theta_1 - theta_2)` `= cos(theta_1 + theta_2)`, 整理得到 `lambda` 满足下面的三次方程: `lambda^2 (a^2 + b^2 + c^2) = a^2 b^2 c^2 + 2 lambda^3`. 解出 `lambda` 后, 再代入 `2 S = sqrt(a^2 b^2 - (bm a * bm b)^2) + sqrt(b^2 c^2 - (bm b * bm c)^2) + sqrt(c^2 a^2 - (bm c * bm a)^2)` `= sqrt(a^2 b^2 - lambda^2) + sqrt(b^2 c^2 - lambda^2) + sqrt(c^2 a^2 - lambda^2)`, 得到面积的最大值.

Euler 线与九点圆

三角形的外心 `O`, 重心 `G`, 垂心 `H` 满足 `vec(OH) = 3 vec(OG)`. 点 `O, G, H` 所在的直线称为 Euler 线.

取三角形的外心 `O` 为原点, 不妨令其外接圆的半径为 1, 则三角形三个顶点 `A, B, C` 的坐标可设为 `(cos theta_i, sin theta_i)`, `i = 1, 2, 3`. 因为 `G` 是重心, 有 `vec(OG) = 1/3(sum cos theta_i, sum sin theta_i)`. 记 `H'` 坐标为 `(sum cos theta_i, sum sin theta_i)`, 从而 `vec(OH') = 3 vec(OG)`. 下证 `H` 与 `H'` 重合, 这只需说明 `H'` 是 `triangle ABC` 的垂心: `vec(AH') * vec(BC)` `= (cos theta_3+cos theta_2, sin theta_3+sin theta_2)` `* (cos theta_3-cos theta_2, sin theta_3-sin theta_2)` `= cos^2 theta_3 - cos^2 theta_2 + sin^2 theta_3 - sin^2 theta_2` `= 0`. 同理 `vec(BH') * vec(AC) = 0`, 因此 `H'` 是 `triangle ABC` 的垂心. 证毕.

若三角形的外心和重心的存在性已证, 上面的证明也可作为三角形垂心存在的证明.

三角形内心与外心距离的 Euler 公式 设三角形的内切圆与外接圆的半径分别为 `r, R`, 两圆圆心距离为 `d`, 则 `d^2 = R^2 - 2 R r`. 整理得 `1/r = 1/(R+d) + 1/(R-d)`. 推论: `R ge 2r`.

设 `triangle ABC` 的内心, 外心分别为 `I, O`, 由内心的齐次坐标, `vec(OI) = 1/(a+b+c)(a vec(OA)+b vec(OB)+c vec(OC))`, 其中 `a, b, c` 分别是边 `BC, CA, AB` 的长. 注意到 `2 vec(OA)*vec(OB) = vec(OA)^2+vec(OB)^2-vec(AB)^2` `= 2R^2 - c^2`, 有 `d^2 = vec(OI)^2` `= 1/(a+b+c)^2 [a^2 vec(OA)^2+b^2 vec(OB)^2+c^2 vec(OC)^2 + 2(a b vec(OA)*vec(OB) + b c vec(OB)*vec(OC) + c a vec(OC)*vec(OA))]`
`= 1/(a+b+c)^2 [(a^2+b^2+c^2)R^2 + a b(2R^2-c^2) + b c(2R^2-a^2) + c a(2R^2-b^2)]` `= 1/(a+b+c)^2 [(a+b+c)^2 R^2 - (a+b+c)abc]` `= R^2 - (abc)/(a+b+c)`. 由 `triangle ABC` 的面积 `S = (abc)/(4R) = r/2(a+b+c)` 有 `(abc)/(a+b+c) = 2R r`. 所以 `d^2 = R^2 - 2 R r`.

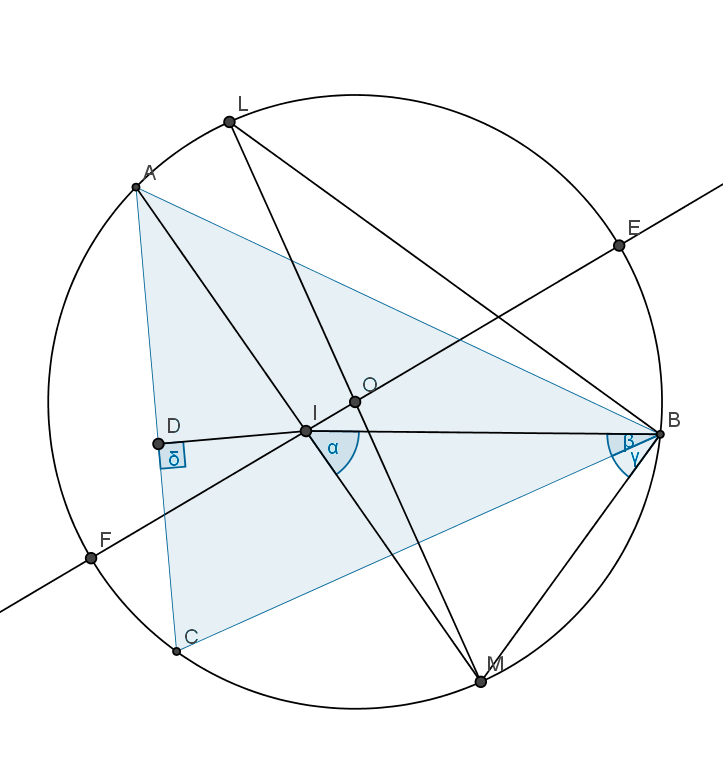设 `triangle ABC` 的内心, 外心分别为 `I, O`, 直线 `IO` 与圆 `O` 交于点 `E, F`, 又设直线 `AI` 与圆 `O` 交于点 `A, M`. 对 `EF` 与 `AM` 应用相交弦定理有 `AI * MI = EI * FI = (R+d)(R-d)`. 另一方面, 作 `DI _|_ AC` 于 `D`, 延长 `MO` 交圆 `O` 于 `L`, 则 `triangle MBL S~ triangle IDA` (`/_ DAI = /_ MAB = /_ L`, `/_ ADI = pi/2 = /_ LBM`), 得到 `AI * MB = ID * LM = 2R r`. 下证两式的左边相等, 从而得到结论. 这只需说明 `MI = MB`. 由 "等边对等角", 这又只需证 `alpha = beta + gamma`. (其中 `alpha := /_ MIB`, `beta := /_ IBC`, `gamma := /_ MBC`). 事实上, 利用角平分线的条件和圆周角相等的性质: `alpha = /_ IBA + /_ IAB` `= beta + /_ IAC` `= beta + gamma`. 证毕.

三角形的内心 `I`, 重心 `G`, 界心 `N` 满足 `vec(I N) = 3 vec(I G)`, 因此 `triangle IGO S~ triangle NGH`.

利用齐次坐标立即得到: `vec(I N) = 1/(a+b+c) (b+c-2a; c+a-2b; a+b-2c)`, `3 vec(I G) = 1/(a+b+c) (a+b+c-3a; a+b+c-3b; a+b+c-3c)`.

到三个顶点的距离之和

设 `triangle ABC` 内部有一点 `M`, `M` 到三边 `a, b, c` 的距离分别为 `x, y, z`, 则 `(abc)/(xyz) ge 4(a/x+b/y+c/z)`.

做法类似于 Euler 公式的证明. 设 `triangle ABC` 的外心为 `O`, 外接圆半径为 `R`, 利用 有 `0 le vec(OM)^2` `= 1/S^2 (S_A^2 vec(OA)^2 + S_B^2 vec(OB)^2 + S_C^2 vec(OC)^2)` `+ 2/S^2(S_B S_C vec(OB)*vec(OC) + S_C S_A vec(OC)*vec(OA) + S_A S_B vec(OA)*vec(OB))` `= R^2/S^2 (S_A^2+S_B^2+S_C^2)` `+ 1/S^2[S_A S_B(2R^2-c) + S_B S_C(2R^2-a^2) + S_C S_A(2R^2-b^2)]` `= R^2/S^2(S_A+S_B+S_C)^2 - (2 S_A S_B S_C)/S^2 (a/x+b/y+c/z)` `= R^2 - (1/4 abc xyz)/(abc//4R)^2 (a/x+b/y+c/z)` `= R^2 [1-(4xyz)/(abc)(a/x+b/y+c/z)]`. 整理即得结论.

Fermat 点 在平面上求一点 `F`, 使之到三角形 `ABC` 的三个顶点的距离之和最短, 并求该最小值. 这个点 `F` 称为 Fermat 点或 Torricelli 点.

若 `triangle ABC` 有一个大于 `2pi//3` 的钝角, 则 `F` 就是该钝角顶点. 否则将 `triangle BCF` 绕点 `C` 顺时针旋转 `pi//3`, 则 `F'B' = FB`. 因为 `triangle CFF'` 是正三角形, 所以 `FF' = FC`. 故 `FA + FB + FC = FA + F'B' + FF' ge AB'`. 设 `CA = b`, `CB = a`, `/_ C = theta`, `AB' = m`, 则 `m = sqrt(a^2+b^2-2a b cos(theta+pi/3))`. 容易看出, 折线 `AFF'B'` 与 `AB'` 重合 当且仅当 `/_ AFC = /_ B'F'C = 2pi//3`, 即 `/_ AFC = /_ BFC = /_ AFB = 2pi//3`. 此时 `F` 到 `ABC` 的三个顶点距离之和达到最小值 `m`.
尺规作图: 以三角形三边向外作正三角形, 这三个正三角形的外接圆交于 Fermat 点.

Erdös-Mordell 不等式 设三角形内部或边界上有一点, 到三个顶点的距离为 `x, y, z`, 到三边的距离为 `l, m, n`, 则 `x+y+z ge 2(l+m+n)`.

(Claudi Alsina and Roger B. Nelsen. A Visual Proof of the Erdos-Mordell Inequality. Forum Geometricorum, Vol. 7 (2007): 99-102.)
三角形的三个顶点记为 `A, B, C`, 其对边分别为 `a, b, c`, `M` 是 `triangle ABC` 内部或边界上一点, 它到 `A, B, C` 的距离分别为 `x, y, z`, 到 `a, b, c` 的距离分别为 `l, m, n`. 过 `M` 作 `MP _|_ AB` 于 `P`, `MQ _|_ AC` 于 `Q`. 现在将 `triangle ABC` 放大 `x` 倍, `triangle APM` 放大 `b` 倍, `triangle AQM` 放大 `c` 倍, 按下图拼合: 由于原图中 `/_ PMQ + /_PAQ = pi`, 所以得到的图形是一个直角梯形, 我们有: `a x ge b n + c m`. 同理 `b y ge c l + a n`, `quad c z ge a m + b l`. 利用均值不等式, `x + y + z` `ge b/a n + c/a m + c/b l + a/b n + a/c m + b/c l` `= (b/a+a/b)n + (c/a+a/c)m + (c/b+b/c)l` `ge 2(l + m + n)`.

四边形

婆罗摩笈多公式 设平面上一四边形的四边长按顺时针依次为 `a, b, c, d`, 其周长的一半为 `p = (a+b+c+d)//2`, 又设其一组对角之和为 `theta`, 则四边形的面积为 `S = sqrt((p-a)(p-b)(p-c)(p-d) - a b c d cos^2{:theta/2:})`. 注意当一组对角之和为 `theta` 时, 另一组对角之和为 `2pi-theta`; 特别当四边形内接于圆时, 根号内的 `cos` 项等于零.

设 `a, b` 的夹角为 `A`, `c, d` 的夹角为 `C`. 四边形被对角线分成边长为 `a, b, l` 和 `c, d, l` 的两个三角形, 由余弦定理, `l^2 = a^2 + b^2 - 2 a b cos A = c^2 + d^2 - 2 c d cos C`, 即 `a^2 + b^2 - c^2 - d^2 = 2(a b cos A - c d cos C)`. 另一方面, `4S = 2(a b sin A + c d sin C)`. 以上两式平方后相加, `(a^2+b^2-c^2-d^2)^2 + 16S^2 = 4(a^2 b^2 + c^2 d^2)` `- 8a b c d(cos A cos C - sin A sin C)`, 于是 `16S^2 = 4(a^2 b^2 + c^2 d^2) - (a^2+b^2-c^2-d^2)^2` `- 8a b c d cos theta` `= 4(a b + c d)^2 - 8a b c d - (a^2+b^2-c^2-d^2)^2` `- 8a b c d (2cos^2{:theta/2:} - 1)`, 得到 `16(S^2+a b c d cos^2{:theta/2:})` `= [2(a b+c d) + a^2+b^2-c^2-d^2][2(a b+c d) - (a^2+b^2-c^2-d^2)]` `= [(a+b)^2 - (c-d)^2][(c+d)^2 - (a-b)^2]` `= (a+b+c-d)(a+b-c+d)(a-b+c+d)(-a+b+c+d)`. 即得所证.

平行四边形四边长的平方和 = 对角线长的平方和.

用向量轻松证明: `|bm a+bm b|^2 + |bm a-bm b|^2` `= 2(|bm a|^2 + |bm b|^2)`.

Apollonius 定理 设三角形三边长为 `a, b, c`, 则边 `a` 上的中线长 `m_a` 满足: `4 m_a^2 = 2(b^2+c^2)-a^2`.

平面上任意四边形四边长的平方和 = 对角线长的平方和 + 4 × 对角线中点连线长度的平方.

设四边形 `ABCD` 中, `AC, BD` 的中点分别为 `M, N`. 在 `triangle NAC`, `triangle ABD`, `triangle CBD` 中分别使用上述推论, `4 MN^2 = 2(AN^2+CN^2)-AC^2`,
`4 AN^2 = 2(AB^2+AD^2)-BD^2`,
`4 CN^2 = 2(CB^2+CD^2)-BD^2`. 将后两个式子代入第一式右边, 整理得 `AB^2+BC^2+CD^2+DA^2` `= AC^2+BD^2+4MN^2`.

Ptolemy 定理 (Hipparchus) 平面四边形的两条对角线乘积 ≤ 两组对边乘积之和, 等号成立当且仅当该四边形内接于圆.

在四边形 `ABCD` 中, 作相似三角形 `triangle ABE S~ triangle ACD`, 有 `AB * CD = BE * AC`. 又由两组边成比例, 易证 `triangle ABC S~ triangle AED`, 有 `BC * AD = ED * AC`. 两式相加, `AB * CD + BC * AD` `= (BE+ED)*AC` `ge BD * AC`. 等号成立当且仅当 `E` 落在 `BD` 上, 即 `/_ ABE = /_ ACD`, 即四边形 `ABCD` 内接于圆.

复数证明. 用 `a, b, c, d in CC` 表示四边形的四个顶点, 有 `|(a-c)(b-d)|` `= |(a-b)(c-d) + (a-d)(b-c)|` `le |(a-b)(c-d)| + |(a-d)(b-c)|`. 其中等号成立当且仅当 `"arg"(a-b)(c-d) = "arg"(a-d)(b-c)`. 即 `"arg"((a-b)(c-d))/((a-d)(b-c)) = 0`. 即 `"arg"(a-b)/(a-d) + "arg"(c-d)/(c-b) = pi`. 这指出四边形的对角互补, 因此内接于圆.

Ptolemy 定理的三角形式 若四个角 `alpha + beta + gamma + delta = pi`, 则 `sin alpha sin gamma + sin beta sin delta` `= sin(alpha+beta) sin(beta+gamma)`.

在圆内接四边形 `ABCD` 中, 记 `alpha = /_ CAD = /_ CBD`, `quad beta = /_ BAC = /_ BDC`,
`gamma = /_ ADB = /_ ACB`, `quad delta = /_ ABD = /_ ACD`, 注意到圆周角 `alpha` 所对的弦长 `CD = 2 r sin alpha`, 应用 Ptolemy 定理即得结论.

Euler 定理 在直线上顺次有 `A, C, B, D` 四点, 则 `AD * CB + AC * BD ge AB * CD`, 这是 Ptolemy 定理的退化情形. 特别当等号成立时, 四点构成调和点列, 这时左边两项相等.

等差幂线定理
1. 四面体的一组对边垂直当且仅当另外两组对边的平方和相等;
2. 平面上四边形的对角线相互垂直当且仅当两组对边的平方和相等.

任取空间中一点 `O`, 分别用 `bm a, bm b, bm c, bm d` 记 `vec(OA), vec(OB), vec(OC), vec(OD)`, 则 `vec(AC) * vec(BD)` `= (bm a-bm c) * (bm b-bm d)` `= bm a * bm b + bm c * bm d - bm a * bm d - bm b * bm c` `= -1/2[(bm a-bm b)^2 + (bm c-bm d)^2 - (bm a-bm d)^2 - (bm b-bm c)^2]` `= -1/2(AB^2 + CD^2 - AD^2 - BC^2)`. 于是 `AC _|_ BD iff AB^2 + CD^2 = AD^2 + BC^2`.

四点共圆判定
1. 到一点距离相等的四点共圆;
2. 四边形对角互补, 四点共圆;
3. 线段 `A B` 同侧有两个点 `C, D`, 若 `/_ ACB = /_ ADB`, 则四点共圆;
4. 圆幂逆定理;
5. Ptolemy 逆定理;

3. 在 `AB` 另一侧作这两个角的补角, 设为 `E`, 由 2 知 `ABEC` 和 `ABED` 分别四点共圆, 从而 `ABCD` 四点共圆.

不借助圆, 也可以由两组相似三角形证明 2 和 3 的等价性: 先设四边形 `ABCD` 中 `/_BAD` 和 `/_BCD` 互补. 延长 `BC` 到 `E`, 使得 `/_CDE = /_ADB`. 于是由 `/_DCE = /_ DAB` 知道, `triangle DCE ~ triangle DAB`. 这推出 `(DE)/(CD) = (DB)/(DA)`. 于是 `triangle EDB ~ triangle CDA`, 从而 `/_CAD = /_CBD`. 从三角形内角和 180 度中扣除掉一组相等对顶角后, 即 `/_ACB = /_ADB`. 反向的证明只需把上述证明倒过来写即可.

杂例

`triangle ABC` 中, `/_A = 2 /_B`, `D` 为 `AB` 中点,
1. 若 `/_ADC = 60^@`, 证明: `/_ACB = 90^@`;
2. 若 `/_ACD = 60^@`, 证明: `/_ACB = 90^@`;

证明 `/_A = 60^@`, 或 `/_B = 30^@`, 或 `/_ACB = 90^@` 是完全等价的.
1. 在 `triangle ACD` 和 `triangle BCD` 中分别使用正弦定理, `(sin 2B)/(CD) = (sin(120^@-2B))/(AD)`, `quad (sin B)/(CD) = (sin(60^@-B))/(BD)`. 于是 `(sin 2B)/(sin B) = (sin(120^@-2B))/(sin(60^@-B))`,
   `cos B = cos(60^@-B) = 1/2 cos B + sqrt3/2 sin B`,
   `tan B = 1/sqrt3`. 因为三角形内角和为 `180^@`, 所以 `0 lt /_B lt 60^@`. 于是 `/_B = 30^@`.
   纯几何证明: 作 `CE _|_ AB` 于 `E`, 取 `BC` 中点 `F`. 则 `CD = DE//cos 60^@ = 2DE`, `AC = 2DF` (因为 `DF` 是中位线). 下证 `DE = DF`, 从而 `CD = AC`, 从而 `/_A = /_ADC = 60^@`.
   我们通过 `/_DEF = /_DFE` 说明这一点. 在直角三角形 `BEC` 中, `EF = BF`, 故 `/_DEF = /_B`; 另一方面 `/_DFE = /_BDF - /_DEF` `= /_A - /_B = /_B`. 证毕.
2. 同样由正弦定理得到 `(sin 2B)/(sin B) = (sin 60^@)/(sin(120^@-3B))`,
   `sin(2A+60^@) + sin(A+60^@) = sqrt3/2`. ??

几何中的物理方法

杠杆原理 和 Ceva 定理等价, 其核心思想是, 要使点 `G` 为三角形物理重心 (区别于几何重心), 应该怎样在顶点处分配质量.
设有 `triangle ABC`, `P, Q, R` 分别在直线 `AB, BC, CA` 上, 且 `AP, BQ, CR` 交于物理重心 `G`. 此时 `P, Q, R` 分别为 `BC, CA, AB` 重心, `A, B, C` 的质量满足 `m_A AR = m_B BR`, `m_B BP = m_C CP`, `m_C CQ = m_A AQ`, 因此 `(AR * BP * CQ)/(BR * CP * AQ)` `= (m_B * m_C * m_A )/(m_A * m_B * m_C)` `= 1`.