圆的切线

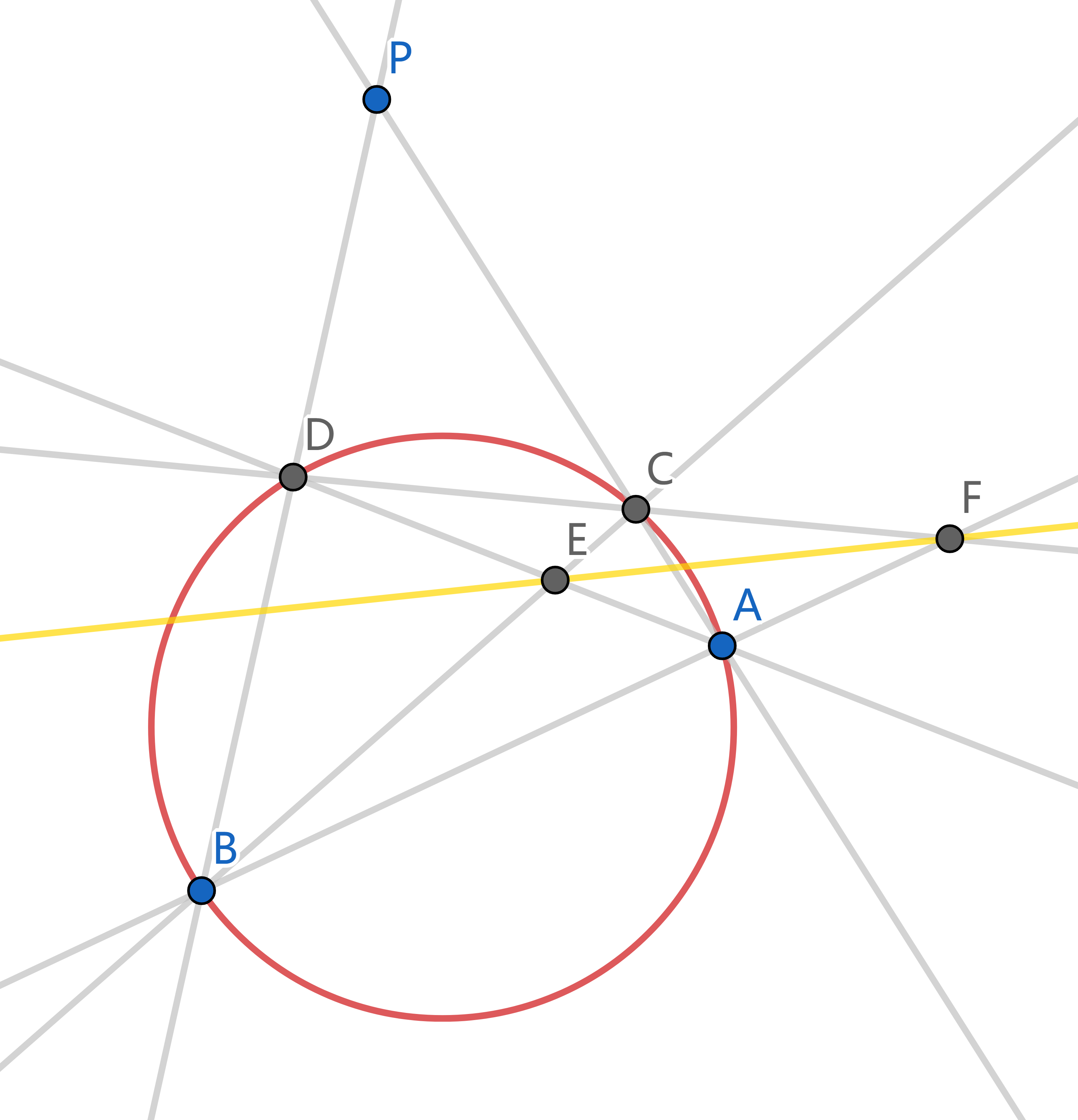
过不在圆上的一点 `P`, 只用直尺作出 `P` 关于圆的极线. 如果 `P` 在圆外, 连接 `P` 到极线与圆的交点就得到两切线.

过 `P` 作圆的两割线, 交圆于 `A, B, C, D` 四点. 这四点确定一个完全四边形, 其中一组对边交于 `P`. 设另外两组对边交于 `E, F`, 则 `EF` 就是极线.

[来自群友 幂零群、太阳花] [圆规x2, 直尺x1] 过圆上一点 `P` 作切线.

    在圆 `O` 上任取一点 `A`, 使得 `O, A, P` 不共线. 作圆 `AP`, 交圆 `O` 于 `P, B`; 作圆 `PB`, 交圆 `A` 于 `B, C`.
  1. 下证 `CP` 就是圆 `O` 的切线. 这只需说明 `/_ CPO = 90^@`: 连接 `PA, PB`, `/_ CPO` 被分为三个角. 我们证明这三个角之和等于 `90^@`.
    1. `triangle PAB S= triangle PAC (SSS)`, 所以 `PA` 平分 `/_BPC`. 设 `/_ BPC = 2alpha`.
    2. `AB = AP` 所以 `/_ ABP = /_ APB = alpha`.
    3. 作圆 `O` 的直径 `PD`. `ABDP` 四点共圆, 所以 `/_ ADP = /_ ABP = alpha`. 由于 `DP` 是直径, 所以 `/_ ADP + /_APD = 90^@`. 于是 `/_ CPO` `= /_APC + /_APD` `= alpha + /_ APD` `= /_ ADP + /_ APD` `= 90^@`.
  2. 进一步设圆 `A` 交直线 `OP` 于 `P, E`, 圆 `P` 交圆 `O` 于 `B, F`. 下证 `C, A, E, F` 四点共线.
    1. 由 1. 知 `/_ CPE = 90^@` 所以 `CE` 是圆 `A` 直径, 这说明 `C, A, E` 共线.
    2. 又 `triangle BPO S= triangle FPO (SSS)`, 所以 `/_ BAF = /_ BPF = 2 /_ BPO`. 又在圆 `A` 中 `/_ BAC = 2/_ BPC`, 所以 `/_ BAF + /_ BAC` `= 2 (/_BPO + /_BPC)` `= 2 /_ CPO = 180^@`. 即 `C, A, F` 共线.

阿氏圆与反演

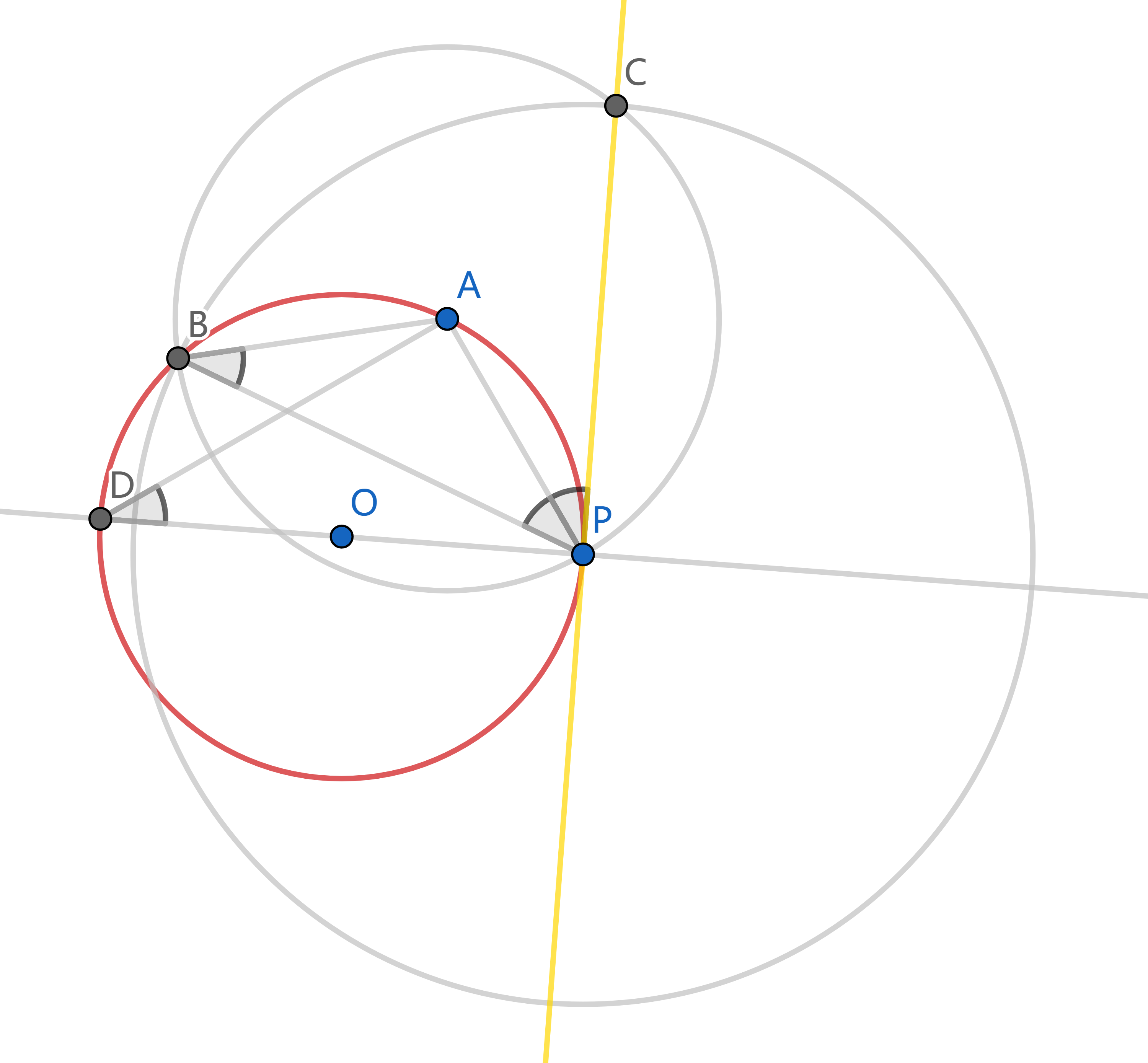
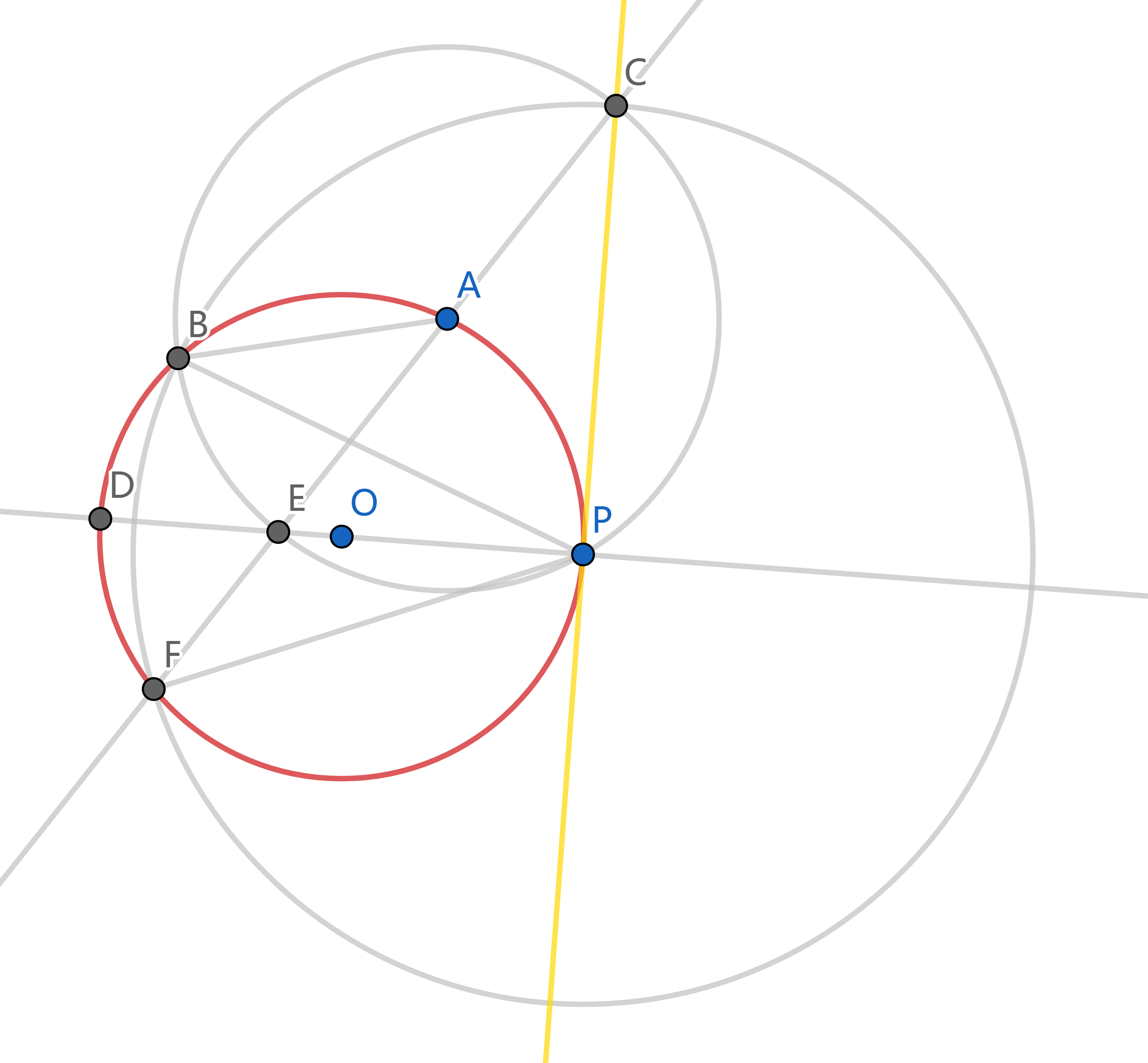
Apollonius 圆 (阿氏圆) 平面上到两定点距离之比为常数 `k` (`k gt 0`, `k != 1`) 的点的轨迹为圆.

设这两个定点为 `A, B`, 线段 `AB` 长为 `l`. 若平面上一点 `R` 满足 `RA = k RB`, 则在直线 `AB` 上可取一点 `O`, 使得 `triangle ORA S~ triangle OBR`. 由相似关系得 `OA * OB = OR^2`. 又 `OA = (OA)/(OR) * (OR)/(OB) * OB = k^2 OB`,
`OA = OB +- l` (`k gt 1` 时取 `+`, `0 lt k lt 1` 时取 `-`), 由此解得的 `OA, OB, OR` 均可用常数 `k, l` 表示, 即 `O` 点的位置与 `OR` 的长度均为定值, 因此 `R` 的轨迹为一圆.

反演变换 设圆 `O` 的半径为 `r`. 观察上图, `A, B` 两点位于 `O` 出发的同一条射线上, 且 `OA * OB = r^2`, 我们称 `A, B` 关于圆 `O` 互为反演, `O` 为反演中心, `r` 为反演半径, 圆 `O` 称为反演的参考圆. 显然, 一个点的反演的反演是其自身. 反演变换的全体不动点就是参考圆上的点.

反演变换将广义圆映为广义圆 除了将一个点映为另一个点, 反演变换也可以将点集映为点集. 常见情形如下:
反演前 反演后
不过反演中心的圆 仍是一个不过反演中心的圆
过反演中心的圆 不过反演中心的直线
过反演中心的直线 它自身
可以为平面引入一个无穷远点 `oo`, 规定反演中心的像是 `oo`. 直线可以视为过 `oo` 的, 半径无穷大的圆. 这样一来, 以上结论简记为: 反演变换将广义圆映为广义圆. 由于对应点在同一直线上, 圆与它的反演圆关于反演中心位似.

反演变换是反向保角的 两条曲线的夹角 (交点处切线的夹角) 在反演变换后保持不变, 但角的定向发生改变 (顺时针变为逆时针).

正交圆的反演像是自身 广义圆在反演变换下的像是自身当且仅当它是参考圆, 或与参考圆正交 (夹角为直角). 一个特殊的正交情形是, 广义圆是通过反演中心的直线.

  1. `rArr`: 因为参考圆上的点都是不动点, 所以参考圆的反演像是自身. 下设变换前的广义圆 `C` 与参考圆 `O` 不重合. 若圆 `C` 完全位于圆 `O` 外部, 则它的像完全位于圆 `O` 内部, 反之亦然. 但圆 `C` 的像是自身, 因此圆 `C` 与圆 `O` 必有交点. 假设两圆的夹角不是直角, 则反演后角的定向改变, 圆 `C` 不可能保持不动; 因此两圆夹角必为直角.
  2. `lArr`: 反之若广义圆 `C` 与参考圆正交, 则由保角性, 反演像仍与参考圆正交, 且两个交点在反演下不动. 由于过两个交点与参考圆正交的广义圆是唯一的 (在两个交点处作参考圆的切线, 切线交点即为所求的圆心), 所以圆 `C` 保持不动.

既然将直线视为特殊的圆, 我们也可以定义关于直线的反演. 为了找到点 `P` 关于直线 `l` 的反演像, 过点 `P` 作两个圆与直线 `l` 正交 (只需圆心在 `l` 上, 作出的圆就会与 `l` 正交), 则 `P` 的像必为这两个圆的另一个交点, 即点 `P` 关于直线 `l` 的对称点.

过不在圆 `O` 上的一点 `A` 可作无数个圆与圆 `O` 正交.

[来自 言、我是阳光开朗的小白] 在圆 `O` 上任取一点 `B` 作为交点. 作圆 `O` 在 `B` 处的切线 `l`, 由正交性, 所求的圆心必定在直线 `l` 上. 但这个圆又过 `A, B` 两点, 所以它的圆心还在 `AB` 中垂线上. 取两直线交点即为所求圆心.

反演变换保持反演关系 设点 `A, B` 关于圆 `C` 互为反演, 现在将 `A, B`, 圆 `C` 一起关于另一个圆 `O` 反演, 则反演像 `A', B'` 关于圆 `C'` 仍互为反演.

过 `A` 可以作无数个圆与圆 `C` 正交, 由于正交圆的反演像是自身, 所以这些圆都通过点 `B`. 任取其中两个圆 `D, E`, 由保角性, 它们关于圆 `O` 反演后的像 `D', E'` 仍与 `C'` 正交. 而 `A', B'` 是这两个圆的交点, 因此关于圆 `C'` 互为反演.

在复平面上, 反演变换是分式线性变换 (Möbius map) 的一个特例. 分式线性变换是指: `f(z) = (a z+b)/(c z+d)`, `quad a, b, c, d in CC`, `quad a d - b c != 0`.

设 `f(z)` 表示点 `z` 关于以 `s = a+b"i"` 为心, `r` 为半径的圆的反演. 先设 `s = 0`, 有 `f(z) = r^2//z`. 一般情形的反演可以先平移到原点进行, 再平移回去, 即 `f(z) = r^2/(z-s) + s` `= (s z+r^2-s^2)/(z-s)`, 这是分式线性变换.
反之, 对任意分式线性变换 `f(z) = (a z+b)/(c z+d)`, 于是当 `c != 0` 时, `f(z) = 1/c((b c - a d)/(c z+d) + a)`, 相当于反演变换与平移、伸缩变换的复合.