曲边梯形不等式

Hadamard 不等式 (曲边梯形不等式) 设 `f` 是 `[a, b]` 上可积的下凸函数, 则 `f((a+b)/2) le 1/(b-a) int_a^b f(x) dx le (f(a)+f(b))/2`. 当 `f` 严格凸且 `a lt b` 时, 不等号严格成立. 这个不等式的几何意义是, `f` 的图像在 `[a,b]` 上围成的曲边梯形面积 大于它在 `x = (a+b)/2` 处的内切梯形面积, 但小于它的外接梯形面积.

记 `I = 1/(b-a) int_a^b f(x) dx`, 令 `x = a + t(b-a) = (1-t)a + t b`, 则 `I = int_0^1 f[(1-t)a+t b] dt` `le int_0^1 [(1-t) f(a) + t f(b)] dt` `= (f(a)+f(b))/2`. 另一方面, 令 `x = a+b-s`, `(b-a) I = int_a^b f(a+b-s) "d"s` `= 1/2 int_a^b [f(x) + f(a+b-x)] dx` `ge int_a^b f((x+a+b-x)/2) dx` `= (b-a)f((a+b)/2)`.

对数均值不等式 (ALG 不等式, 奥利给不等式) 设 `a, b` 是不相等的正数, 则 `sqrt(a b) lt (a-b)/(ln a - ln b) lt (a+b)/2`, 即 `A gt L gt G`. 这一不等式刻画了 `ln {:a/b:}` 的上下界.

积分学的证明. 在 `[u,v]` 上对 `f(x) = "e"^x` 应用 Hadamard 不等式, 得到对数均值不等式的指数形式: `"e"^((u+v)/2) lt ("e"^v-"e"^u)/(v-u) lt ("e"^u+"e"^v)/2`, 令 `"e"^u = a`, `"e"^v = b` 即得证.

又一积分学的证明. 分别在 `[a, b]` 和 `[a, sqrt(a b)]` 上对 `f(x) = 1/x` 应用 Hadamard 不等式, 有 `2/(a+b) lt (ln b - ln a)/(b-a)`,
`(ln sqrt(a b) - ln a)/(sqrt(a b) - a) lt (a^-1 + (a b)^(-1/2))/2`. 整理即得结论.

(比值法) 微分学的证明. 先证明 `b = 1` 的情形: `sqrt x lt (x-1)/(ln x) lt (x+1)/2`, 即证 `sqrt x - 1/sqrt x lt ln x lt 2(x-1)/(x+1)`, `quad 0 lt x lt 1`,
`2(x-1)/(x+1) lt ln x lt sqrt x - 1/sqrt x`, `quad x gt 1`. 换言之, `ln x` 的值介于 `sqrt x - 1/sqrt x` 和 `2(x-1)/(x+1)` 之间, 且三者的函数图像在 `x=1` 时相交. 设 `f(x) = sqrt x - 1/sqrt x - ln x`, `quad g(x) = 2 (x-1)/(x+1) - ln x`. 计算知 `f(1) = g(1) = 0`, 且在 `(0, +oo)` 上 `f'(x) gt 0`, `g'(x) lt 0`. 于是 成立.
取 `x = a/b`, 再在不等号两边同乘 `b` 即得证.

[来自 我是完全的無法理解] `sum_(k=1)^n 1/(n+k) gt ln 2 - 1/(4n)`.

由于左边 `xx 2 = sum_(k=1)^n(1/(n+k) + 1/(n+k-1)) - 1/(2n)`, 只需证 `sum_(k=1)^n (1/(n+k) + 1/(n+k-1)) gt 2 ln 2`. 这只需由对数均值不等式 `1/2(1/(n+k) + 1/(n+k-1)) gt ln(n+k) - ln(n+k-1)` 求和即得.

Stirling 公式青春版 [来自 崔尚斌《数学分析》] `sqrt n (n/"e")^n * "e"^(7//8) lt n! lt sqrt n (n/"e")^n * "e"`. 注: 标配版的 Stirling 公式是指 `n! ~ sqrt(2pi n) (n/"e")^n`, 我们有 `7/8 lt ln sqrt(2pi) lt 1`.

运用曲边梯形不等式估计积分 `int_1^n ln x dx`. 一方面 `int_1^n ln x dx` `gt sum_(k=1)^(n-1) (ln k + ln(k+1))/2` `= ln(n!) - 1/2 ln n`, 另一方面, `int_1^n ln x dx` `= int_1^(3//2) + int_(3//2)^(n-1//2) + int_(n-1//2)^n` 对于中间一项有 `int_(3//2)^(n-1//2) ln x dx` `lt sum_(k=2)^(n-1) ln k` `= ln(n!) - ln n`. 左右两项分别用 `x=1` 和 `x=n` 处的切线近似, 有 `int_1^(3//2) ln x dx` `lt 1/2 * 底 * 高` `= 1/2 * 1/2 * 1/2` `= 1/8`,
`int_(n-1//2)^n ln x dx` `lt 1/2 * 高 * (上底 + 下底)` `= 1/2 * 1/2 * (ln n + ln n - 1/(2n))` `= 1/2 ln n - 1/(8n)`. 以上三式相加得 `int_1^n ln x dx` `lt ln(n!) - 1/2 ln n - 1/(8n) + 1/8`. 整理得 `-1/8 lt ln(n!) - int_1^n ln x dx - 1/2 ln n lt 0`. 代入 `int_1^n ln x dx` `= n (ln n - 1) + 1` 得到 `7/8 lt ln(n!) - n ln n + n - 1/2 ln n lt 1`. 取指数即得结论.

一阶估计

幂函数的一阶估计

Bernoulli 不等式 设实数 `x gt -1`, `a ge 0`, 则 `(1+x)^a ge 1 + a x`, `quad a ge 1`,
`(1+x)^a le 1 + a x`, `quad 0 le a le 1`. 等号成立当且仅当 `a = 0, 1` (曲线与直线重合) 或 `x = 0` (曲线与直线相切).

在 `0` 到 `x` 的区间上 Taylor 展开 `(1+x)^a = 1 + a x + (a(a-1))/2 xi^2` 即得结论.

Bernoulli 不等式是很基础的不等式, 这里就 `a` 等于正整数 `n` 的情形给出归纳法证明: `n = 1` 时 `(1+x)^1 = 1 + 1*x` 成立. 假设结论对正整数 `n-1` 成立, 则 `(1+x)^n` `ge (1+x) (1 + (n-1) x)` `= 1 + n x + (n-1)x^2` `ge 1 + n x`. 等号成立当且仅当 `n = 1` 或 `x = 0`.

设 `a, b gt 0`, `r gt 1`, 证明 `(a+b)^r gt a^r + b^r`.

(比值法) 设 `x = a/b`, 只需证 `x gt 0` 时 `(1+x)^r - x^r gt 1`. 设 `f(x) = (1+x)^r - x^r`, 则 `f(0) = 1`, 且 `x gt 0` 时 `f'(x) = r(1+x)^(r-1) - r x^(r-1) gt 0`, 因此不等式成立.

指对数函数的一阶估计

指对数函数的一阶估计 在 `0` 到 `x` 的区间上 Taylor 展开, `"e"^x = 1 + x + xi^2/2 ge 1 + x`,
`ln(1+x) = x - eta^2/2 le x`.

  1. `1 + x le "e"^x le 1//(1-x)`, 等号成立当且仅当 `x = 0` (右半不等式只对 `x lt 1` 成立);
  2. `1-1//x le ln x le x-1`, 等号成立当且仅当 `x = 1`;
  3. `x gt 0` 时, `1/(x+1) lt ln (1+1/x) lt 1/x`, 即 `(1+1/x)^x lt "e" lt (1+1/x)^(x+1)`.
  1. 设 `f(x) = "e"^x - x - 1`, 则 `f(0) = 0`, 且 `f'(x) = "e"^x - 1 { lt 0, if x lt 0; gt 0, if x gt 0; :}` 于是 `f(x) ge 0`. 换元 `x mapsto -x` 得 `"e"^-x ge 1 - x`, 当 `x lt 1` 时两边取倒数即得结论.
  2. 由 1. 取对数得 `x ge ln(1+x)`, 换元 `x mapsto x-1`, 得 `x - 1 ge ln x`; 再换元 `x mapsto 1//x`, 得 `1//x - 1 ge -ln x`.

注意, 要证的不等式中含有分式时, 一般要将其线性化为整式, 再求导证明. 如 `"e"^x le 1//(1-x)` 直接求导只会越求越繁.

    `x^x` 的两个估计 `x gt 0` 时有
  1. `x^x ge "e"^(x-1)`, 等号成立当且仅当 `x = 1`;
  2. `x ln x gt x "e"^-x - 2//"e"`.
  1. 取对数, 两边同除以 `x`, 就化为对数函数的一阶估计;
  2. (过渡法) 这是因为左边的最小值等于右边的最大值. 这相当于以常数函数作为证明的过渡.
  1. `prod_(n ge 1) (1 + 1/3^n) le sqrt "e"`;
  2. `1/2 3/4 5/6 cdots = 0`.
    利用不等式 `1 + x le "e"^x`,
  1. `prod_(n ge 1) (1 + 1/3^n)` `le prod_(n ge 1) "e"^(3^-n)` `= exp(sum_(n ge 1) 3^-n)` `= sqrt "e"`.
  2. 原式等于 `(1-1/2)(1-1/4)(1-1/6)` `le "e"^(-1/2-1/4-1/6 cdots)` `to "e"^-oo = 0`.
  1. `x gt 1` 时, `x^2-1 gt 2 x ln x`;
  2. `x gt 0` 时, `ln(1+x) gt (2x)/(x+2)`.
  1. 令 `f(x) = x^2 - 1 - 2x ln x`, 则 `f(1) = 0`, 而 `f'(x) = 2x - 2 - 2 ln x` `= 2(x-1 - ln x) gt 0`, 故结论成立. 也可以在对数均值不等式中取 `a = x^2`, `b = 1`, 则 `sqrt(x^2) lt (x^2 - 1)/(ln x^2)`, 整理即得结果.
  3. 只需说明 `x = 0` 时两边都等于 `0`, 而 `x gt 0` 时 `ln(1+x) - (2x)/(x+2)` 的导数大于零即可. 也可以对 `a = 1+x`, `b = 1` 使用对数均值不等式.

`2x "e"^(x-1) ge (x^2+1)(ln x+1)`.

    `x = 1` 时, 等号成立. 使用多项式过渡, 只需证: 左边 `gt 2x^2 gt` 右边, `quad 0 lt x lt 1`;
    左边 `gt x^3 + x gt` 右边, `quad x gt 1`.
  1. 先设 `0 lt x lt 1`, 显然 `2x "e"^(x-1) gt 2x^2`. 令 `f(x) = 2x^2 - (x^2+1)(ln x+1)`, 则 `f(1) = 0`, `f'(x) = x - 1/x - 2x ln x` `= x(1-1/x^2 - ln x^2) le 0`.
  2. 再设 `x gt 1`, 显然 `x^3 + x gt (x^2+1)(ln x+1)`. 令 `g(x) = 2"e"^(x-1) - x^2 - 1`, 则 `g(1) = 0`, `g'(x) = 2"e"^(x-1) - 2x gt 0`.

`"e"^x gt ln x + 2x + 1/sqrt 2`.

??

Lambert W 函数

    Lambert W 函数: `x "e"^x` 的反函数.
  1. 在不等式 `"e"^t ge t+1` 中令 `t = a x + ln x` (`a != 0`) 得 `x "e"^(a x) ge a x + ln x + 1`, 等号成立当且仅当 `t = 0`. 从而得到: 不等式 `x"e"^(a x) ge b x + ln x + 1` 对所有 `x gt 0` 成立当且仅当 `a ge b`.
  2. 现在考虑等号成立的条件 `a x + ln x = 0`, 或 `x "e"^(a x) = 1`. 记 `x "e"^x` 的反函数为 Lambert W 函数 `W(x)`, 即 `W(x) "e"^(W(x)) = x`. 于是原方程化为 `a x"e"^(a x) = a`, 得到 `x = W(a)//a`.
  3. 用 Lambert W 函数求解 `a/x + ln x = 0`, 或 `x "e"^(a/x) = 1`. 两边取倒数再同乘 `-a` 得 `-a/x "e"^(-a/x) = -a`, 于是 `-a/x = W(-a)`, `x = -a // W(-a)`.
  4. 用 Lambert W 函数求解 `x^x = a`, 或 `x ln x = ln a`. 方程化为 `"e"^(ln x) ln x = ln a`, 于是 `ln x = W(ln a)`, `x = "e"^(W(ln a))`.

极值点偏移

[高中数学：极值点偏移问题有什么好的解决办法？]

极值点偏移 设函数 `f` 有两个零点 `a lt b`, 且在开区间 `(a, b)` 上有唯一的极值点 `x_0`. 考虑区间中点 `(a+b)//2`, 若 `x_0` 位于中点左侧 (右侧), 则称 `f` 在 `(a, b)` 上极值点左偏 (右偏).

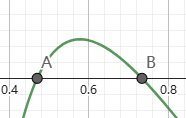
极值点左偏

为研究极值点偏移, 构造奇函数 `F(x) = f(x_0 + x) - f(x_0 - x)`, 其中 `F(0) = 0`. 如果 `f` 关于 `x_0` 对称, 则 `F` 应该恒等于零. 若 `F` 单调 (如单增), 则对任意 `x gt 0` 有 `F(x) ge 0`. 特别地 `F(x_0-a) ge 0`, 即 `f(2x_0-a) = f(2x_0-a) - f(a) ge 0 = f(b)` 由极值点 `x_0` 的唯一性知道, `f` 在 `[x_0, b]` 上单调. 进一步假定存在充分大的数 `M`, 使得 `f` 在 `[x_0, M]` 上单调 (如单增), 则上式推出 `2 x_0 - a ge b`, 即 `x_0 ge (a+b)//2`, 因此极值点右偏.

判定 `F(x)` 单调性的常用方法是考察其导数的正负: `F'(x) = f'(x_0 + x) color(red)(+) f'(x_0 - x)`, 注意中间的加号.

我们将极值点偏移情况总结为下表, 它的规律和乘法法则一致, 应该是容易记忆的:
`x_0` 是 `f` 的 `f` 在 `[x_0, M]` 上 `F` 的单调性 极值点偏移情况
极小值点 单增 (+) 单增 (+) 右偏 (+)
极小值点 单增 (+) 单减 (-) 左偏 (-)
极大值点 单减 (-) 单增 (+) 左偏 (-)
极大值点 单减 (-) 单减 (-) 右偏 (+)

若 `f(x) = "e"^x - a x` 有两个不同的零点 `x_1`, `x_2`, 则 `x_1 x_2 lt 1`, `quad 2 lt x_1 + x_2 lt 2 ln a`.

使用对数均值不等式. 由题意 `"e"^(x_1) = a x_1`, `quad "e"^(x_2) = a x_2`, 取对数得 `x_1 = ln a + ln x_1`, `quad x_2 = ln a + ln x_2`. 因此 `x_1 - x_2 = ln x_1 - ln x_2`. 由对数均值不等式有 `sqrt(x_1 x_2) lt 1 lt (x_1+x_2)/2`, 从而得 `x_1 x_2 lt 1`, `x_1 + x_2 gt 2`. 再由 得到 `x_1 + x_2 = 2 ln a + ln x_1 x_2 lt 2 ln a`.

    下面我们运用标准的极值点偏移方法证明 `x_1 + x_2 lt 2 ln a`.
  1. 求极值点 不妨设 `x_1 lt x_2`, 由题意知 `f` 在 `[x_1, x_2]` 上有唯一极小值点 `x_0`, 它满足 `f'(x_0) = "e"^(x_0) - a = 0`, 即 `x_0 = ln a`.
  2. 构造对称函数, 并利用单调性 令 `F(x) = f(x_0 + x) - f(x_0 - x)`, 有 `F'(x) = "e"^(x_0+x) + "e"^(x_0-x) - 2 a` `ge 2("e"^(x_0) - a) = 0`. 上式等号只在 `x = 0` 时成立, 故 `F` 严格单调增. 由 `F` 的单调性有 `F(x_0 - x_1) gt 0`, 即 `f(2x_0 - x_1) gt f(x_2)`; 又 `f` 在 `(x_0, x_2)` 上严格单调增, 由 `f` 的单调性有 `x_1 + x_2 lt 2 x_0 = 2 ln a`.
  3. 适当的换元, 或对方程变形 我们再证明 `x_1 x_2 lt 1`, 即证 `ln x_1 + ln x_2 lt 0`.
    `f(x)` 的零点满足方程 `"e"^x = a x`, 即 `x = ln x + ln a`. 换元 `y = ln x`, 则 `"e"^y = y + ln a`. 令 `g(y) = "e"^y - y - ln a` 的两个零点为 `y_1, y_2`, 则 `g(y)` 有极小值点 `y_0 = 0`. 下证 `g'(y_0+y) + g'(y_0-y) ge 0`, 即证 `"e"^(y_0+y) + "e"^(y_0-y) ge 2`, 上式由均值不等式即可得到. 因此由极值点偏移的结论知 `y_1 + y_2 lt 0`, 即 `x_1 x_2 lt 1`.
  4. 我们再证明 `x_1 + x_2 gt 2`, 为此令 `h(x) = x - ln x - ln a`, 它有极小值点 `x_0 = 1`. 下证 `h'(x_0+x) + h'(x_0-x) le 0`, 即证 `1/(x_0+x) + 1/(x_0-x) ge 2`. 上式用均值不等式 `2/(1//a+1//b) le (a+b)/2` 即得证.

若 `f(x) = ln x + 2/x - a` 有两个不同的零点 `x_1, x_2`, 则 `x_1 + x_2 gt 4`, `quad x_1 x_2 gt 4`.

由题意 `ln x_1 = a - 2/x_1`, `quad ln x_2 = a - 2/x_2`, 因此 `ln x_1^-1 = 2 x_1^-1 - a`, `quad ln x_2^-1 = 2 x_2^-1 - a`. 应用对数均值不等式, `2/(x_1+x_2) lt sqrt(x_1^-1 x_2^-1)` `lt (x_1^-1 - x_2^-1)/(ln x_1^-1 - ln x_2^-1) = 1/2`, 即 `x_1 + x_2 gt 4`, `x_1 x_2 gt 4`.

使用极值点偏移法证明 `x_1 x_2 gt 4`.
换元 `y = ln x`, 令 `g(y) = f(x) = y + 2 "e"^-y - a`, 令 `y_1, y_2` 是 `g(y)` 的两个零点, 原问题化为证明 `y_1 + y_2 gt 2 ln 2`.
`g(y)` 有极小值点 `y_0 = ln 2`. 下证 `g'(y_0+y) + g'(y_0-y) le 0`, 即证 `"e"^(-y_0-y) + "e"^(-y_0+y) le 1`. 上式由均值不等式即可得到. 最后由极值点偏移的结论有 `y_1 + y_2 gt 2 ln 2`. 有了 `x_1 x_2 gt 4`, 自然就有 `x_1 + x_2 ge 2 sqrt(x_1 x_2) gt 4`.
我们也可以直接应用极值点偏移证明 `x_1 + x_2 gt 4`. 这是因为 `f` 有极小值点 `x_0 = 2`. 且 `f'(x_0+x) + f'(x_0-x) = (2x_0)/((x_0+x)(x_0-x)) - 2/(x_0+x)^2 - 2/(x_0+x)^2`, 利用均值不等式可证上式 `le 0`.

[来自群友 Lucifer 成都2023高二月考] 已知函数 `f(x) = ln x - a x` 存在两个不同的零点 `x_1, x_2`, 求证 `1/sqrt x_1 + 1/sqrt x_2 lt 2/sqrt "e"`.

    使用极值点偏移法.
  1. 换元 `y = 1//sqrt x`, 即 `x = 1//y^2`, 于是 `f(x) = ln x - a x = -2 ln y - a//y^2`, 令 `y_1, y_2` 是这个新函数的两个零点, 原问题化为证明 `y_1 + y_2 lt 2//sqrt"e"`.
  2. 如果直接令 `g(y) = -2 ln y - a//y^2`, 则它的极值点是 `sqrt a`, 而不是我们期待的 `1//sqrt"e"`. 强行做下去只能得出下界 `y_1 + y_2 gt 2 sqrt a`, 这不是我们想要的. 因此我们对方程 `-2 ln y - a//y^2 = 0` 变形得到 `y^2 ln y = -a/2`, 再令 `g(y) = y^2 ln y`. 此时 `g'(y) = 2y ln y + y`, `g(y)` 有极小值点 `y_0 = 1//sqrt "e"`.
  3. 下证 `g'(y_0+y) + g'(y_0-y) ge 0`, 即证 `h(y) = (y_0+y) ln(y_0+y) + (y_0-y)ln(y_0-y) + y_0 ge 0`. 注意到 `h(0) = g'(y_0) = 0`, 因此只需证明 `h(y)` 在 `y=0` 处取得最小值. 为此求得 `h'(y) = ln(y_0+y) - ln(y_0-y)`, 发现 `h'(y)` 在 `y gt 0` 时为正, `y lt 0` 时为负, 因而 `h(0)` 确实是 `h` 的唯一极小值, 不等式成立.
  4. 由极值点偏移的结论知 `y_1 + y_2 lt 2 y_0 = 2//sqrt"e"`.

Gronwall 不等式

这是一类在数理方程中常用的积分不等式 [参见 Gronwall 不等式], 其形式非常灵活多变, 我们只介绍最基本的情形.

    微分不等式 设 `f` 在 `x ge 0` 时连续,
  1. 若 `f` 在 `x gt 0` 时可微, 给定初值条件 `f(0) = 1`, 解微分不等式 `f' lt f`;
  2. 若 `f` 在 `x gt 0` 时二阶可微, 给定初值条件 `f(0) = 1` 和 `f'(0) le 1`, 解微分不等式 `f'' lt f`.
  1. `f' lt f` 两边同乘积分因子 `"e"^-x`, 有 `f' "e"^-x - f "e"^-x lt 0`, 即 `"d"/dx (f "e"^-x) lt 0`. 令 `g(x) = f(x) "e"^-x`, 则 `g(0) = 1`, `g' lt 0`, 因此 `g le 1`, 即 `f le "e"^x`.
  2. 设 `g = "e"^-x f`, 则 `g' = "e"^-x (f' - f)`,
    `g'' = "e"^-x (f - 2f' + f'')` `lt 2 "e"^-x(f - f') = -2 g'`.     下面解不等式 `g'' lt -2 g'`. 设 `h = "e"^(2x) g'`, 则 `h' = "e"^(2x) (2g' + g'') lt 0`, 故 `h lt h(0) = g'(0) = f'(0) - f(0) le 0`. 这推出 `g' lt 0`, 故 `g le g(0) = f(0) = 1`, 即 `f le "e"^x`.

Gronwall 引理 设函数 `g in L[a, b]`, `p in C[a, b]`, 函数 `y` 满足微分不等式 `y'(t) le g(t) + p(t) y(t)`, `quad AA t in [a, b]`, 则 `y(t) le y(a) P(t) + int_a^t g(s) P(t) // P(s) "d"s`. 其中 `P(t) = exp(int_a^t p(u) "d"u)`, 因此 `P(t) // P(s) = exp(int_s^t p(u) "d"u)`.

在微分不等式两边同乘积分因子 `Phi(t) = 1/(P(t)) = exp(-int_a^t p(u) "d"u)` 得 `"d"/dt (y(t) Phi(t)) le g(t) Phi(t)`. 上式两边在 `[a, t]` 上积分得 `y(t) Phi(t) - y(a) le int_a^t g(s) Phi(s) "d"s`, 整理即得结论.

    (Gronwall 不等式, 1919) 设 `g in L[a,b]`, `f, p in C[a, b]`, `p(t) ge 0`, 且 `f(t) le g(t) + int_a^t p(s) f(s) "d"s`, `quad AA t in [a,b]`, 则
  1. `f(t) le g(t) + int_a^t p(s) g(s) P(t) // P(s) "d"s`, `P(t)` 的含义同上.
  2. 若 `g` 连续可微, 上式分部积分可得 `f(t) le g(a) P(t) + int_a^t g'(s) P(t) // P(s) "d"s`.
  3. 若 `g` 单调增, 结论简化为 `f(t) le g(t) P(t)`.

    4. 1. 记 `y(t) = int_a^t p(s) f(s) "d"s`, 由已知 `f(t) le g(t) + y(t)`, 于是由 `p` 非负有 `y'(t) = p(t) f(t) le p(t) g(t) + p(t) y(t)`. 由引理, `y(t) le int_a^t p(s) g(s) P(t)//P(s) "d"s`. 再由 `f(t) le g(t) + y(t)` 即得结论.
    3. 把 1. 中的 `g(s)` 放大为 `g(t)` 再化简即可. 注意 `int_a^t p(s)//P(s) "d"s = 1 - 1//P(t)`.

    Jensen 不等式 (积分形式)

    Jensen 不等式的积分形式 设 `x(t)` 在 `[a, b]` 上可积, 值域含于区间 `I`; `f` 是区间 `I` 上连续的下凸函数; `w(t)` 在 `[a, b]` 上可积, `w(t) gt 0`, 且 `int_a^b w(t) dt = 1`, 则 `f(int_a^b w(t) x(t) dt)` `le int_a^b w(t) f(x(t)) dt`. 特别取 `w(t) -= 1/(b-a)` 得, `f(1/(b-a) int_a^b x(t) dt)` `le 1/(b-a) int_a^b f(x(t)) dt`. 取 `g = -f` 知, 对上凸函数成立反向的不等号.
    [欧阳资考. 2011. 利用凸函数证明积分不等式. 高等教育, 第 107 期]

    易知不等式中出现的积分都有意义. 将 `[a, b]` `n` 等分, 记 `h = (b-a)//n`, `t_k = a+k h`, `x_k = x(t_k)`, `w_k = w(t_k)`, `y_k = w_k/(sum_(k=1)^n w_k)`, `k = 1, 2, cdots, n`. 因为 `f` 为上凸函数, 由 Jensen 不等式, `f(sum_(k=1)^n x_k y_k)` `le sum_(k=1)^n f(x_k) y_k`, 即 `f((sum_(k=1)^n w_k x_k h)/(sum_(k=1)^n w_k h))` `le (sum_(k=1)^n w_k f(x_k) h)/(sum_(k=1)^n w_k h)`. 令 `n to oo`, 注意 `f` 的连续性, 极限符号可转移到 `f` 的括号内. 从而由定积分的定义即得结果.

    假设定理中的 `x(t)` 在 `[a,b]` 上单调增, 于是 `f @ x` 仍是 `[a,b]` 上的下凸函数, 类比 Hadamard 不等式的证明方法可以得到, `1/(b-a) int_a^b f(x(t)) dt le (f(x(a)) + f(x(b)))/2`.

    `bm p` 方可积 设 `p ge 1`, 函数 `f` 在定义域 `[a,b]` 上只有有限个瑕点, 且 `f` 在任意不含这些瑕点的闭子区间上都 Riemann 可积. 如果 `|f(x)|^p` 在 `[a,b]` 上广义 Riemann 可积, 即瑕积分 `int_a^b |f(x)|^p dx lt oo`, 则称 `f` 在 `[a,b]` 上 `bm p` 方可积. 特别当 `p = 1` 时, 称 `f` 在 `[a,b]` 上绝对可积, `p = 2` 时, 称 `f` 在 `[a,b]` 上平方可积.

    `p` 方可积函数的任意线性组合也 `p` 方可积.

    设 `f,g` 在 `[a,b]` 上 `p` 方可积, 显然对任意常数 `c`, 函数 `c f` 也在 `[a,b]` 上 `p` 方可积. 下证函数 `f+-g` 在 `[a,b]` 上 `p` 方可积. 只需注意对 `AA x in [a,b]` 有 `|f(x) +- g(x)|^p` `le (|f(x)|+|g(x)|)^p` `le (2 max{|f(x)|, |g(x)|})^p` `= 2^p max{|f(x)|^p, |g(x)|^p}` `le 2^p (|f(x)|^p + |g(x)|^p)`, 据此立得结论.

    设 `1 le p lt q`, 若函数 `f` 在 `[a,b]` 上 `q` 方可积, 则它也在 `[a,b]` 上 `p` 方可积.

    Hölder 不等式 设 `p, q gt 1` 且 `1/p+1/q = 1`. 如果 `f` 在 `[a,b]` 上 `p` 方可积, `g` 在 `[a,b]` 上 `q` 方可积, 则乘积 `f g` 在 `[a,b]` 上绝对可积, 且 `int_a^b |f(x)g(x)| dx` `le (int_a^b |f(x)|^p dx)^(1/p) (int_a^b |g(x)|^q dx)^(1/q)`. 特别取 `p = q = 2`, 得到 Cauchy 不等式 `int_a^b |f(x) g(x)| dx` `le sqrt(int_a^b |f(x)|^2 dx) sqrt(int_a^b |g(x)|^2 dx)`.

    记 `int_a^b |f(x)|^p dx = A`, `int_a^b |g(x)|^q dx = B`. 使用 Young 不等式, 对 `AA x in [a,b]` 有 `(|f(x)|^p/A)^(1/p) (|g(x)|^q/B)^(1/q)` `le 1/p |f(x)|^p/A + 1/q |g(x)|^q/B`. 因为不等式右端函数在 `[a,b]` 上广义可积, 所以左端也可以. 积分得 `1/(A^(1/p) B^(1/q)) int_a^b |f(x) g(x)| dx` `le 1/p + 1/q = 1`. 所以原不等式成立.

    `f` 是 `[a, b]` 上的非负可积函数, 证明: `(int_a^b f(x) sin lambda x dx)^2` `+ (int_a^b f(x) cos lambda x dx)^2` `le (int_a^b f(x) dx)^2`.

    应用 Cauchy 不等式, `(int_a^b f(x) dx)^2 - (int_a^b f(x) cos lambda x dx)^2` `= int_a^b f(x) (1 + cos lambda x) dx int_a^b f(x) (1 - cos lambda x) dx` `ge (int_a^b f(x) sqrt((1+cos lambda x)(1-cos lambda x)) dx)^2` `ge (int_a^b f(x) sin lambda x dx)^2`.

    设 `f in C[0, 1]`, 且 `AA x in [0, 1]`, `int_x^1 f(t) dt ge (1-x^2)/2`. 证明: `int_0^1 f(x)^2 dx ge 1/3`.

      1, 2 是两个较松的下界, 3 是正解.
    1. 在 `[0, 1]` 上应用 Cauchy 不等式, `int_0^1 f(x)^2 dx int_0^1 1^2 dx` `ge (int_0^1 f(x) dx)^2` `ge (int_0^1 (1-0^2)/2 dx)^2 = 1/4`.
    2. 在 `[x, 1]` 上应用 Cauchy 不等式, `((1-x^2)/2)^2` `le (int_x^1 f(t) dt)^2` `le int_x^1 1^2 dt int_x^1 f(t)^2 dt` `le (1-x) int_0^1 f(t)^2 dt`. 于是 `int_0^1 f(t)^2 dt ge "sup" (1-x^2)(1+x)//4 = 8//27`.
    3. [群友 我是卑微不敢说话的飞矢不动] 将已知的不等式在 `[0, 1]` 上积分, `1/3 = int_0^1 (1-x^2)/2 dx` `le int_0^1 int_x^1 f(t) dt dx` `= int_0^1 int_0^t f(t) dx dt` `= int_0^1 t f(t) dt`, 从而 `int_0^1 f(x)^2 dx int_0^1 x^2 dx` `ge (int_0^1 x f(x) dx)^2` `ge 1/9`, 即 `int_0^1 f(x)^2 dx ge 1//3`. 注意 `f(x) -= x` 时等号成立, 故 `1//3` 是最优下界.

    [来自群友 千帆过尽，匆忘初心] 设 `f` 在 `[0, 1]` 上有二阶连续导数, 且 `f(0) = f(1) = f'(0) = 0`, `f'(1) = 1`. 证明: `int_0^1 f''(x)^2 dx ge 4`.

    失败的尝试. 直接使用 Cauchy 不等式只能得到一个松的下界: `int_0^1 f''(x)^2 dx` `ge (int_0^1 f''(x) dx)^2/(int_0^1 1^2 dx)` `= (f'(1) - f'(0))^2 = 1`.

    将 `f''(x)` 与一个待定的函数作内积: `int_0^1 f''(x)(x+a) dx` `= (1+a) - int_0^1 f'(x) dx` `= 1+a`,
    `int_0^1 (x+a)^2 dx` `= 1/3 + a + a^2`.     这时使用 Cauchy 不等式: `int_0^1 f''(x)^2 dx` `ge (int_0^1 f''(x)(x+a) dx)^2/(int_0^1 (x+a)^2 dx)` `= (1+a)^2/(1/3 + a + a^2)`. 我们希望上式的右端是 4, 于是 `(1+a)^2 = 4(1/3 + a + a^2)`, 解得 (重根) `a = -1/3`, 证毕.
    这种方法未免有些投机取巧, 而且待定函数的形式 `x+a` 不是一下能猜到的.
    [来自群友 乐正垂星] 这是经典变分问题, 极值条件是 `f'''(x) = 0`. 使用二阶导的 Euler-Lagrange 方程, 代入边界条件知 `f(x) = x^3 - x^2` 时, 积分式取得最小值 `4`. 这时将 `f''(x) = 6x-2` 代入 Cauchy 不等式就得到: `int_0^1 f''(x)^2 dx` `ge (int_0^1 f''(x)(6x-2) dx)^2/(int_0^1 (6x-2)^2 dx)` `= 4`.
    家人们看懂了吗??

    [来自 stack exchange] 设 `f in L[a, b]`, `0 lt m le f(x) le M`. 则 `(int_a^b f(x) dx) (int_a^b dx/(f(x))) le (M+m)^2 / (4 M m) * (b-a)^2`. 注: Cauchy 不等式给出 `(int_a^b f(x) dx) (int_a^b dx/(f(x))) ge (b-a)^2`.

    因为 `m le f le M`, 有 `(f - M)(f - m) le 0` `rArr f + M m // f le M+m`. 两边积分, `int_a^b (f(x) + (M m)/(f(x))) dx` `le (b-a)(M+m)`. 用均值不等式, `2 sqrt((int_a^b f(x) dx) (M m int_a^b dx/(f(x))))` `le int_a^b (f(x) + (M m)/(f(x))) dx` `le (b-a)(M+m)`. 整理即得结论.

    下面两个不等式可以仿照上一章对应不等式来证明.

    Minkowski 不等式 设 `p ge 1`, `f, g` 都在 `[a,b]` 上 `p` 方可积, 则 `(int_a^b |f(x) +- g(x)|^p dx)^(1/p)` `le (int_a^b |f(x)|^p dx)^(1/p) + (int_a^b |g(x)|^p dx)^(1/p)`.

    幂平均值不等式 设 `f` 在 `[a,b]` 上 `p` 方可积, `p ge 1`, 则函数 `(1/(b-a)int_a^b|f(x)|^alpha dx)^(1/alpha)` 关于参数 `alpha` 单调递增.